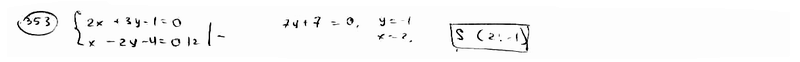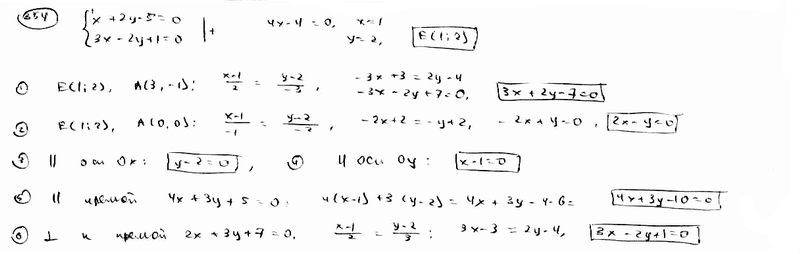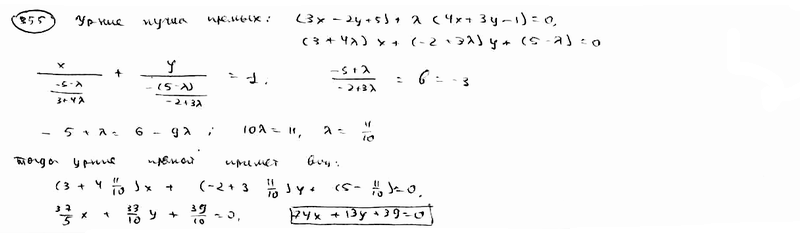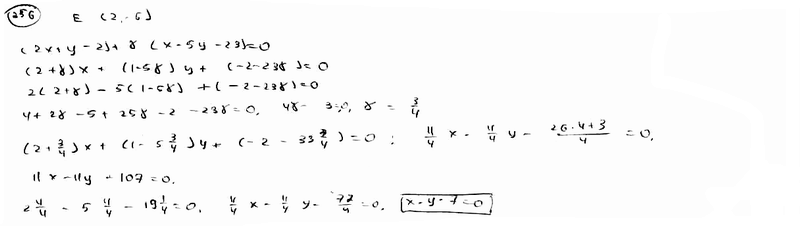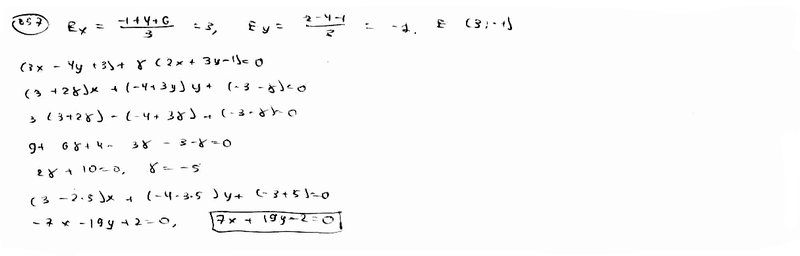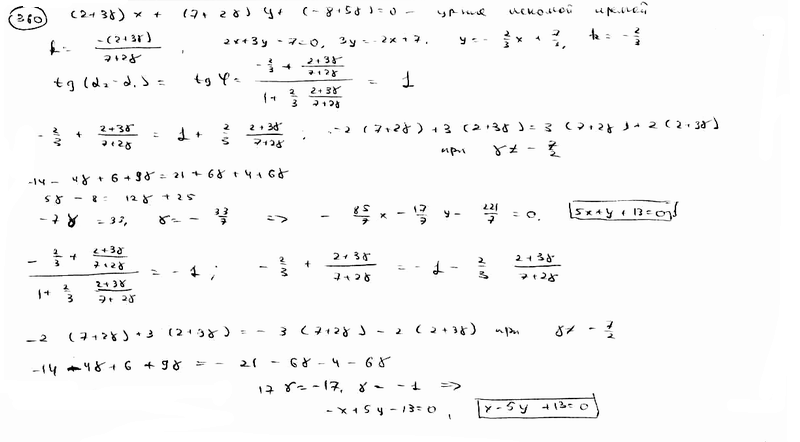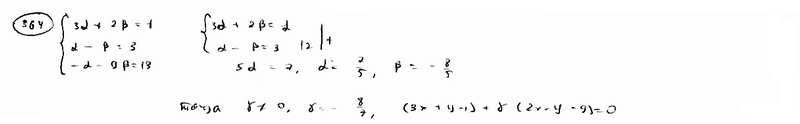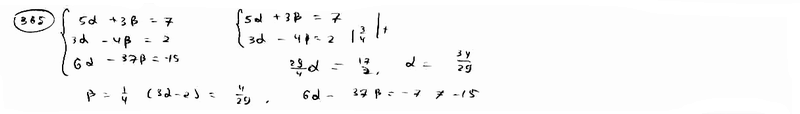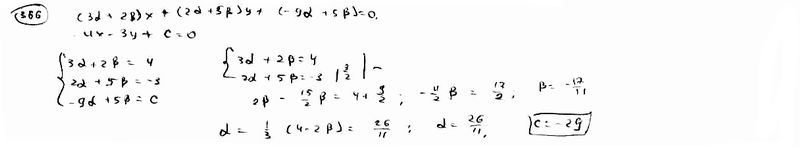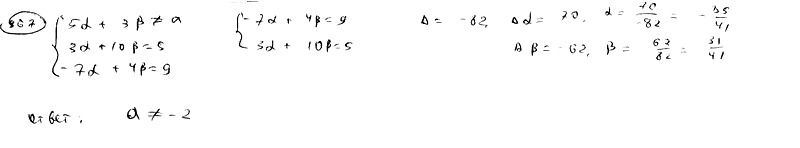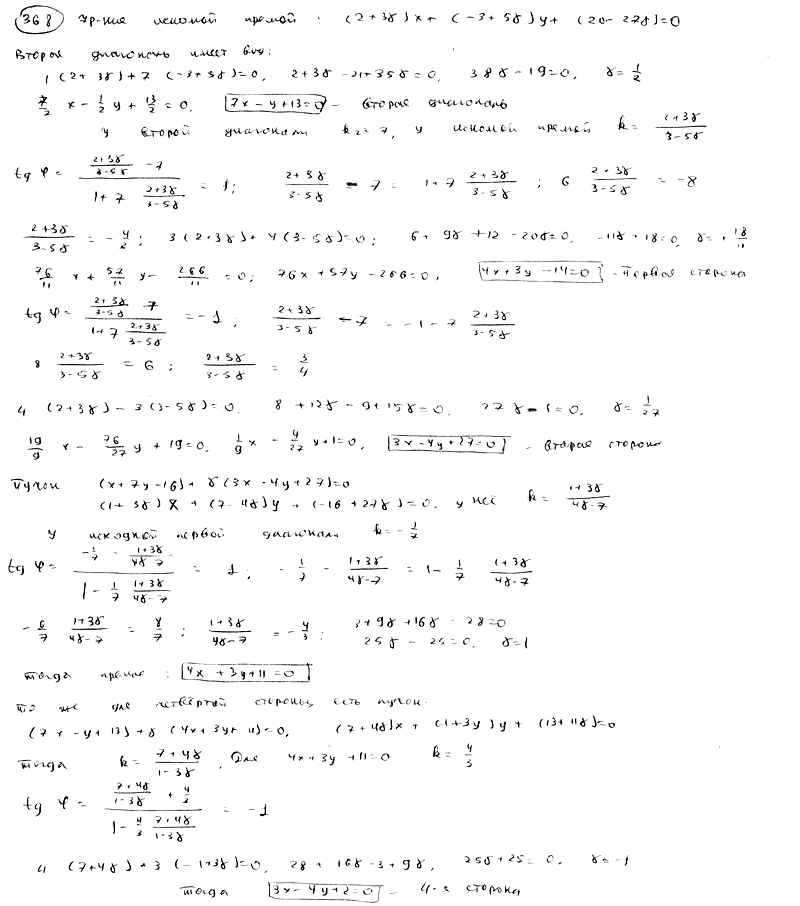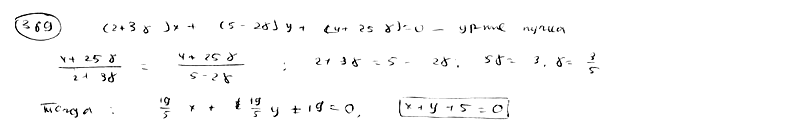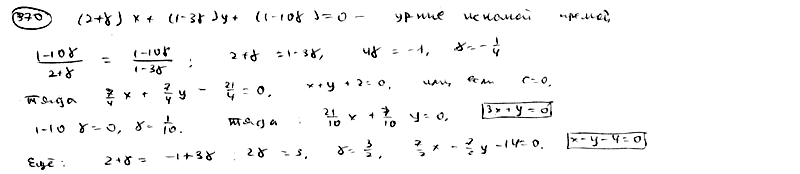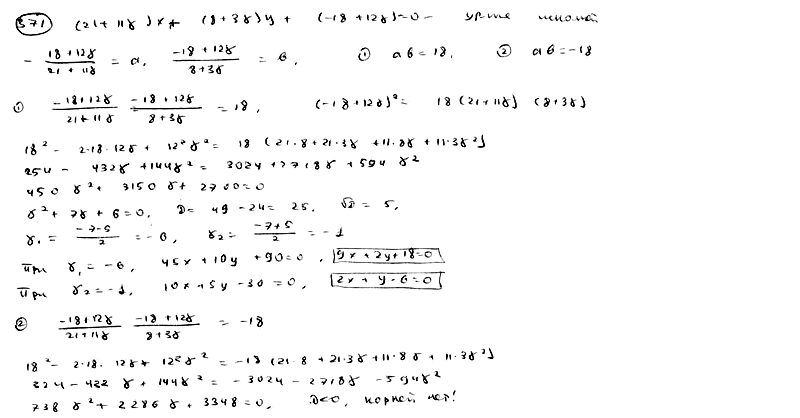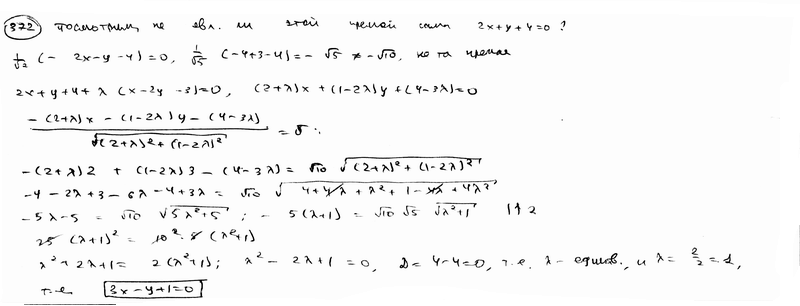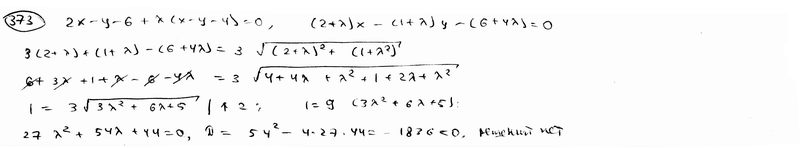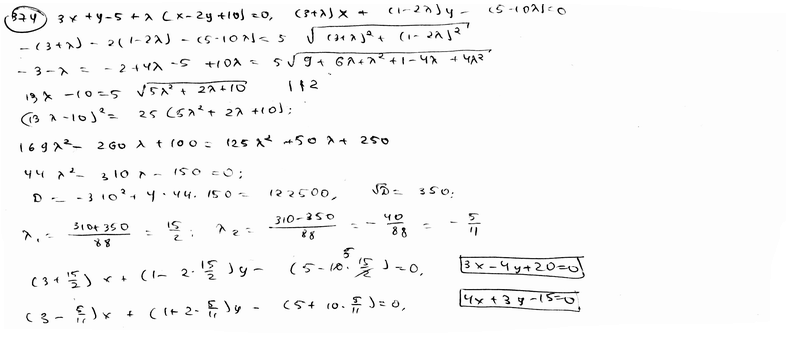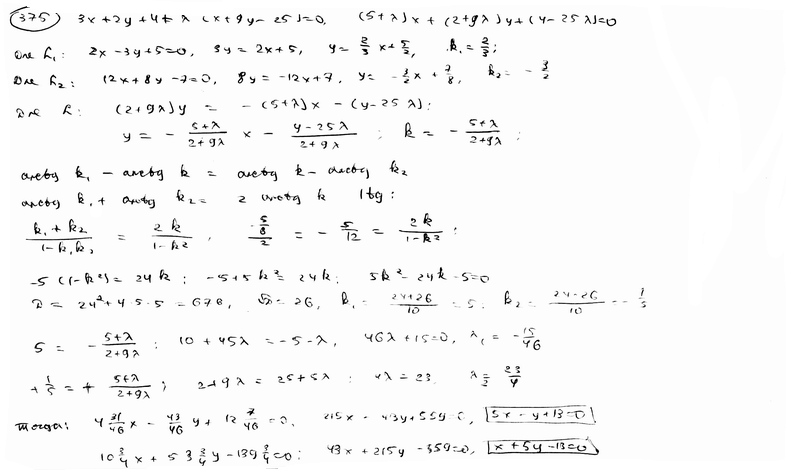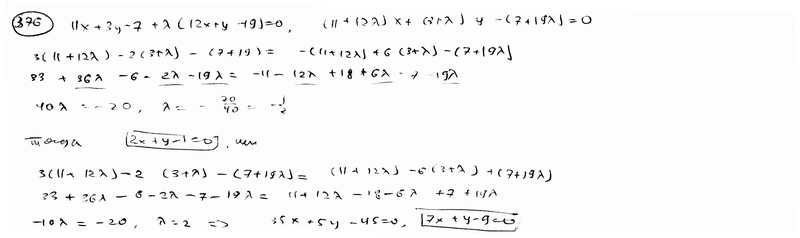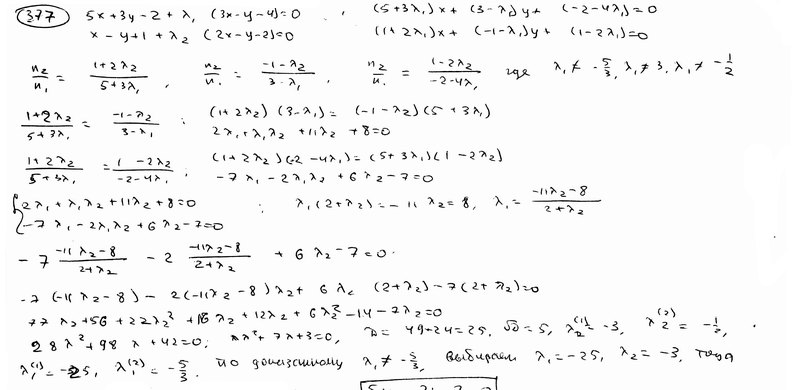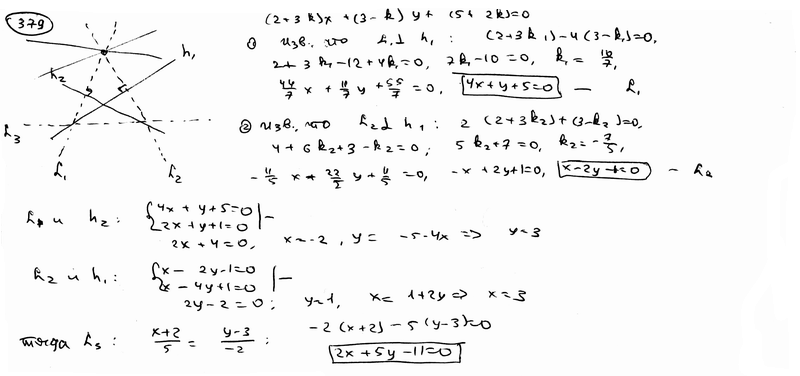- •Предисловие ко второму изданию
- •Часть 1. Аналитическая геометрия на плоскости Глава 1. Простейшие задачи аналитической геометрии на плоскости
- •Глава 1. Ось и отрезок оси. Координаты на прямой
- •Глава 2. Декартовы прямоугольные координаты на плоскости
- •Глава 3. Полярные координаты
- •Глава 4. Направленный отрезок. Проекция отрезка на произвольную ось. Проекции отрезка на координатные оси. Длина и полярный угол отрезка. Расстояние между двумя точками.
- •Глава 5. Деление отрезка в заданном отношении
- •Глава 6. Площадь треугольника
- •Глава 9. Понятие уравнения линии. Задание линии при помощи уравнения
- •Глава 10. Вывод уравнений заранее данных линий
- •Глава 11. Параметрические уравнения линии
- •Часть 3. Линии первого порядка
- •Глава 12. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых
- •Глава 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трех прямых. Уравнение прямой "в отрезках"
- •Глава 14. Нормальное уравнение прямой. Расстояние от точки до прямой
- •Глава 15. Уравнение пучка прямых
- •Глава 16. Полярное уравнение прямой
- •Часть 4. Геометрические свойства линий второго порядка
- •Глава 17. Окружность
- •Глава 18. Эллипс
- •Глава 19. Гипербола
- •Глава 20. Парабола
- •Глава 21. Полярные уравнения эллипса, гиперболы и параболы
- •Глава 22. Диаметры линий второго порядка
- •Глава 5. Упрощение общего уравнения линии второго порядка. Уравнения некоторых кривых
- •Глава 23. Центр линии второго порядка
- •Глава 24. Приведение уравнения центральной линии второго порядка к простейшему виду
- •Глава 25. Приведение параболического уравнения к простейшему виду
- •Глава 26. Уравнение некоторых кривых, встречающихся в математике и ее приложениях
- •Часть 2. Аналитическая геометрия в пространстве Глава 6. Некоторые простейшие задачи аналитической геометрии в пространстве
- •Глава 27. Декартовы прямоугольные координаты в пространстве
- •Глава 28. Расстояние между двумя точками. Деление отрезка в данном отношении
- •Глава 7. Векторная алгебра
- •Глава 29. Понятие вектора. Проекция вектора
- •Глава 34. Двойное векторное произведение
- •Глава 8. Уравнение поверхности и уравнения линии
- •Глава 35. Уравнение поверхности
- •Глава 37. Уравнение цилиндрической поверхности
- •Глава 9. Уравнение плоскости. Уравнения прямой. Уравнения поверхностей второго порядка
- •Глава 38. Общее уравнение плоскости.
Глава 15. Уравнение пучка прямых
|
353 |
|
Найти
центр пучка прямых, данного уравнением
|
|
354 |
|
Найти
уравнение прямой, принадлежащей пучку
прямых
|
|
|
354.1 |
Проходящей через точку А(3; -1); |
|
|
354.2 |
Проходящей через начало координат; |
|
|
354.3 |
Параллельной оси Ox; |
|
|
354.4 |
Параллельной оси Oy; |
|
|
354.5 |
Параллельной
прямой
|
|
|
354.6 |
Перпендикулярной
к прямой
|
|
355 |
|
Составить
уравнение прямой, проходящей через
точку пересечения прямых
|
|
356 |
|
Составить
уравнение прямой, которая проходит
через точку пересечения прямых
|
|
357 |
|
Дано
уравнение пучка прямых
|
|
358 |
|
Дано
уравнение пучка прямых
|
|
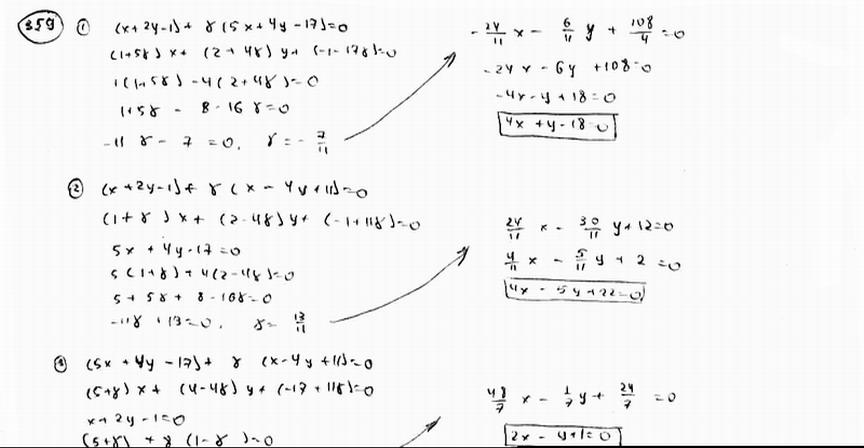
359 |
|
Даны
уравнения сторон треугольника
(ВНИМАНИЕ. ИЗОБРАЖЕНИЕ РЕШЕНИЯ ОБРЕЗАНО ВНИЗУ. РЕШЕНИЕ НЕ ПОЛНОЕ). |
|
360 |
|
Составить
уравнение прямой, проходящей через
точку пересечения прямых
|
|
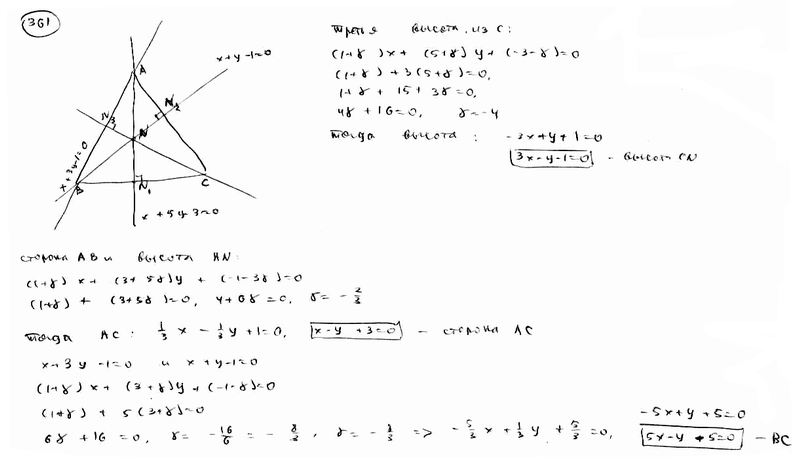
361 |
|
В
треугольнике АВС даны уравнения высоты
AN:
|
|
362 |
|
Составить
уравнения сторон треугольника АВС,
зная одну его вершину А(2; -1), а также
уравнения высоты
|
|
363 |
|
Дано
уравнение пучка прямых
|
|
364 |
|
Дано
уравнение пучка прямых
|
|
365 |
|
Дано
уравнение пучка прямых
|
|
366 |
|
Дано
уравнение пучка прямых
|
|
367 |
|
Дано
уравнение пучка прямых
|
|
368 |
|
Центр
пучка прямых
|
|
369 |
|
Дано
уравнение пучка прямых
|
|
370 |
|
Дано
уравнение пучка прямых
|
|
371 |
|
Дано
уравнение пучка прямых
|
|
372 |
|
Дано
уравнение пучка прямых
|
|
373 |
|
Дано
уравнение пучка прямых
|
|
374 |
|
Составить
уравнение прямой, проходящей через
точку пересечения прямых
|
|
375 |
|
Дано
уравнение пучка прямых
|
|
376 |
|
Составить
уравнение прямой, которая проходит
через точку пересечения прямых
|
|
377 |
|
Даны
уравнения двух пучков прямых
|
|
378 |
|
Стороны
АВ, ВС, CD, DA четырехугольника ABCD заданы
соответственно уравнениями
|
|
379 |
|
Центр
пучка прямых
|