6.6. Метод Гаусса-Жордана решения систем линейных уравнений

Данный метод является модификацией метода исключения. Он также имеет прямой и обратный ходы.

Задачей прямого хода является выяснение существования решения системы и при положительном ответе - приведение ее матрицы к верхнему треугольному виду с единичной диагональю. Для этого на прямом ходе для всех значений i (i = 1,…,n) производится обработка элементов а_ij (j = i,…,n) ведущей строки i и соответствующего элемента b_i вектораB, а также обнуление элементов ведущего столбца i под главной диагональю. Вначале проверяют для диагонального элемента условие а_ii = 0.

Если равенство выполняется, заменяют всю строку i расширенной матрицы на нижележащую k (k > i), у которой элемент столбца i не равен нулю: а_ki  0. В том случае, если такой строки нет, то в рассматриваемой подматрице системы путем эквивалентных преобразований получен нулевой столбец, следовательно, ее определитель равен нулю и у нее и у всей исходной системы не существует единственного решения. Для уменьшения погрешности расчетов желательно при обмене выбирать такую нижележащую строку k (k > i), у которой элемент а_ki столбца i имеет максимальный модуль.

Если диагональный элемент а_ii  0, то все элементы строки i расширенной матрицы делятся на него. После такого преобразования элемент на главной диагонали а_ii будет равен 1. Обнуление элементов столбца i под главной диагональю производится аналогично методу Гаусса - к каждой нижележащей строке k (k > i),прибавляется строка i расширенной матрицы, все элементы которой умножены на коэффициент (-а_ki).

Задачей обратного хода является приведение матрицы системы к диагональному виду. Он выполняется аналогично методу Гаусса. Поскольку перестановок неизвестных не производится и во всех строках уже выполнено деление на диагональный элемент, то решение исходной системы уравнений равно свободному вектору расширенной системы, полученной в результате обратного хода.

Пример 1. Применить метод Гаусса-Жордана для решения той же системы уравнений, что и в примере 1.

Решение. Расширенная матрица системы A_p имеет тот же вид.

Прямой ход.

1. Обработка строки 1. Так как а₁₁= 4  0, то все элементы строки 1 расширенной матрицы делятся на него. Полученная матрица обозначена A_p1. Для обнуления элементов столбца 1 под главной диагональю вторую строку расширенной матрицы складываем с первой, умноженной на коэффициент (-а₂₁) = 5; третью складываем с первой, умноженной на коэффициент (-а₃₁) = 6. В результате получим новый вид расширенной матрицы A_p1:

2. Обработка строки 2. Диагональный элемент а₂₂= 3/4  0, все элементы строки 2 расширенной матрицы делим на него. Полученная матрица обозначена A_p2. Для обнуления элементов столбца 3 под главной диагональю третью строку расширенной матрицы складываем со второй, умноженной на коэффициент (-а₃₂) = (-1/2). В результате получим новый вид расширенной матрицы A_p2:

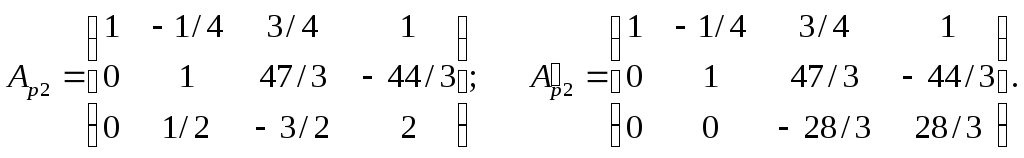
3. Обработка строки 3. Диагональный элемент а₃₃= -28/3  0, все элементы строки 3 делим на него. Поскольку прямой ход завершен, матрицу обозначим A_пр:

Обратный ход. Выполняется аналогично методу Гаусса. В итоге в свободном векторе полученной матрицы A_обр сразу получим искомое решение:

Ответ: х₁= 2; х₂=1; х₃=-1.

Алгоритм метода Гаусса-Жордана несколько упрощен по сравнению с методом Гаусса. В нем исключен поиск главного элемента ведущей строки и смена мест переменных, при которой меняются местами столбцы в матрице системы и необходимо запоминать их порядок в специальном векторе. Однако пересылки элементов выполняются быстро, а операция сравнения все равно используется при проверке элементов на главной диагонали. Отказ от поиска максимального элемента в ведущем столбце может привести к увеличению погрешностей расчетов при делении элементов расширенной строки на малый элемент.

При обнулении элементов в столбце i под главной диагональю для каждой нижележащей строки k (k > i) одно деление сокращается (исключен расчет коэффициента (-а_ki/а_ii)). При этом устраняется (n-i) делений, однако столько же делений затрачивается на преобразование элементов строки i расширенной матрицы, лежащих правее главной диагонали.

Также устранены деления при расчете коэффициентов для обнуления элементов ведущих столбцов над главной диагональю и в конце обратного хода, а также перестановки неизвестных в соответствии с вектором порядка Р.

Выполненный анализ показывает, что трудоемкость метода Гаусса-Жордана примерно совпадает с трудоемкостью метода Гаусса. Сложности их алгоритмов одинаковы.

Вопросы для проверки знаний.

1. Каким образом в методе Гаусса-Жордана обеспечивается ненулевая величина диагонального элемента ведущей строки ?

2. В чем отличие матрицы, получаемой после прямого хода в методе Гаусса-Жордана от аналогичной матрицы в методе Гаусса ?

3. Почему в свободном векторе расширенной матрицы системы после обратного хода сразу получают решение системы ?

Практическое задание.

1. Решить методом Гаусса-Жордана систему линейных уравнений: