6.4. Прямые методы решения систем линейных уравнений. Метод с использованием обратной матрицы и метод Крамера

Среди прямых методов решения, в которых решение системы выражено в формульном виде наиболее известными являются методы:

1) с помощью обратной матрицы,

2) метод Крамера.

1. Метод с использованием обратной матрицы. Векторное решение системы линейных уравнений вида (6.7) можно получить умножая обе части системы слева на обратную матрицу A^-1. Оно имеет вид:

Х = A^-1В (6.10)

где A^-1 матрица, обратная к А. Таким образом, решение системы сводится к решению задачи обращения квадратной матрицы системы А.

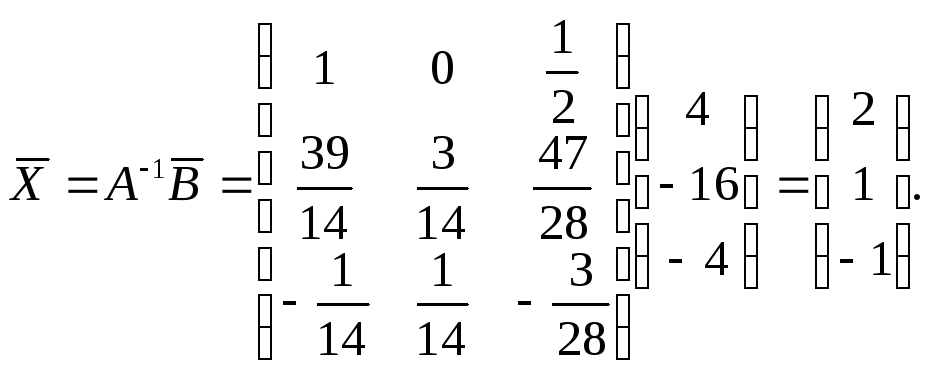
Пример 1. Применить метод с использованием обратной матрицы для решения системы уравнений

у которой матрица совпадает в матрицей А₂ из примера 1 п. 5.5.

Решение. В примере 1 п. 5.5 найдена обратная матрица:

Умножая ее слева на вектор свободных коэффициентов системы, находим ее искомое решение:

Оценка трудоемкости и сложности алгоритма. Определим вначале число необходимых операций при решении системы линейных уравнений с использованием обращения матрицы. Как показано в Главе 5, при использовании сокращенного алгоритма, реализующего метод Гаусса—Жордана, на получение обратной матрицы A^-1 порядка n затрачивается (n–1)²(n+1) умножений и сложений, а также 2(n–1)(n+1) делений. Для получения решения Х обратная матрица должна быть умножена на свободный вектор системыВ. Как показано в Главе 5, данное умножение требует выполнения n² умножений и n(n-1) сложение. В итоге получим, что суммарные количества умножений m(n), сложений s(n) и делений d(n) в алгоритме с использованием обратной матрицы будут следующими:

m(n) = (n–1)²(n+1) + n² = n³ - n² + 1;

s(n) = (n–1)²(n+1) + n(n-1) = n³ - 2n + 1;

d(n)= 2(n–1)(n+1).

Из найденных чисел m(n), s(n) и d(n) следует, наиболее быстро растут числа операций сложения и умножения (n³), сложность алгоритма - кубическая O(n³).

Метод (правило) Крамера представляет каждое неизвестное х_i системы уравнений (6.7) в виде отношения определителей:

х_i = _i /, (6.11)

где _i – вспомогательный определитель матрицы А_i, получающейся из матрицы А заменой i-го столбца столбцом свободных коэффициентов системы В,

 - главный определитель системы (определитель матрицы А).

Пример 2. Применить метод Крамера к решению системы уравнений из примера 1.

Решение. Вначале рассчитаем главный определитель системы  и вспомогательный определители ₁, ₂ и ₃ матриц, получающихся из матрицы А заменой столбцов 1,2,3 столбцом свободных коэффициентов системы.

Подставляя значения определителей в формулу (6.11), находим значения неизвестных:

х₁ = ₁ / = (-56) /(-28) = 2; х₂ = ₂ / = (-28) /(-28) = 1; х₃ = ₃ / = (28) /(-28) = -1.

Оценка сложности алгоритма. Как указано в Главе 5, оптимальные методы расчета определителей имеют максимальную (при ненулевом определителе) сложность О(n³). Поскольку метод Крамера предусматривает расчет (n+1) определителя порядка n, то его сложность будет в лучшем случае при оптимальном расчете определителей иметь полиномиальную сложность четвертой степени: n  О(n³)=О(n⁴). Метод не оптимален, поскольку он имеет сложность, превышающую сложность метода с использованием обратной матрицы. Высокая сложность метода обусловлена тем, что в нем при расчете определителей повторно рассчитываются их одинаковые фрагменты. Поэтому метод Крамера имеет больше теоретическое, чем практическое значение.

Рассмотренные выше прямые методы решения систем линейных уравнений (метод, основанный на обращении матриц и метод Крамера) сохраняют матрицу системы А и ее свободный вектор В в процессе решения. Однако за счет эквивалентного преобразования уравнений системы структура ее матрицы может быть существенно упрощена - сведена к треугольному, а затем диагональному виду. Такой прием позволяет устранить повторную обработку отдельных частей системы, характерную, в частности, для метода Крамера.

Вопросы для проверки знаний.

1. Почему решение системы линейных уравнений ненулевом определителе ее матрицы равно обратной матрице, умноженной на свободный вектор системы ?

2. Докажите, что метод решения системы линейных уравнений порядка n с использованием обратной матрицы может быть реализован алгоритмом со кубической сложностью O(n³).

3. Можно ли применить для решения системы линейных уравнений метод (правило) Крамера, если определитель матрицы системы равен нулю ?

4. Докажите, что метод решения системы линейных уравнений порядка n с использованием по правилу Крамера может быть реализован алгоритмом с полиномиальной сложностью не ниже 4 степени O(n⁴).

5. Почему метод решения системы линейных уравнений порядка n с использованием обратной матрицы при больших n более предпочтителен по сравнению с правилом Крамера ?

Практическое задание.

1. Применить метод с использованием обратной матрицы для решения системы уравнений