
- •Глава 4. Численные методы алгебры. Решение систем лИнейных уравнений
- •4.1. Линейные уравнения. Теоретическое и практическое решения линейных уравнений с одним неизвестным
- •4.2. Системы линейных уравнений. Основные понятия
- •4.3. Определители (детерминанты) квадратных матриц
- •Свойства определителей
- •Расчет определителей
- •4.4. Необходимо и достаточное условие существования решения системы линейных уравнений. Методы решения
- •4.5. Прямые методы решения систем линейных уравнений
- •1. Метод с использованием обратной матрицы.
- •[Править] Метод Гаусса—Жордана
- •[Править] с помощью матрицы алгебраических дополнений
- •[Править] Использование lu/lup-разложения
- •[Править] Примеры [править] Матрица 2х2
- •2.1. Погрешности вычислений на эвм
- •1. Метод Гаусса
- •Будем рассматривать столбцы матрицы X как векторы
- •6. Итерационные методы
[Править] Примеры [править] Матрица 2х2
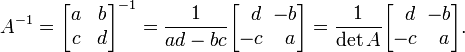
Обращение
матрицы 2х2 возможно только при условии,
что
![]() .
.
![]()
Рассмотрим квадратную матрицу
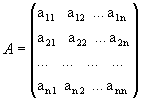 .
.
Обозначим =det A.
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если = 0.
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная матрице А, обозначается через А1, так что В = А1. Обратная матрица вычисляется по формуле
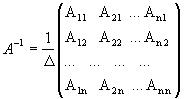 ,
(4.5)
,
(4.5)
где А i j - алгебраические дополнения элементов a i j.
Вычисление обратной матрицы по формуле (4.5) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.
Пример
2.10. Для
матрицы
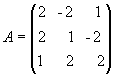 найти
обратную.
найти
обратную.
Решение.
Находим
сначала детерминант матрицы А
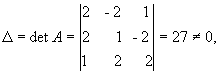 значит,
обратная матрица существует и мы ее
можем найти по формуле:
значит,
обратная матрица существует и мы ее
можем найти по формуле: 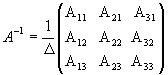 ,
где Аi j
(i,j=1,2,3) - алгебраические дополнения
элементов аi
j исходной
матрицы.
,
где Аi j
(i,j=1,2,3) - алгебраические дополнения
элементов аi
j исходной
матрицы.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
откуда
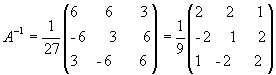 .
.
Пример
2.11. Методом
элементарных преобразований найти
обратную матрицу для матрицы: А=
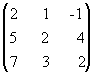 .
.
Решение.
Приписываем
к исходной матрице справа единичную
матрицу того же порядка:
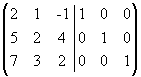 .
С помощью элементарных
преобразований
столбцов приведем левую “половину” к
единичной, совершая одновременно точно
такие преобразования над правой матрицей.
Для этого поменяем местами первый и
второй столбцы:
.
С помощью элементарных
преобразований
столбцов приведем левую “половину” к
единичной, совершая одновременно точно
такие преобразования над правой матрицей.
Для этого поменяем местами первый и
второй столбцы:
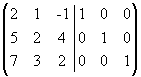
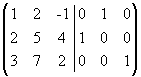 .
К третьему столбцу прибавим первый, а
ко второму - первый, умноженный на -2:
.
К третьему столбцу прибавим первый, а
ко второму - первый, умноженный на -2:
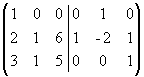 .
Из первого столбца вычтем удвоенный
второй, а из третьего - умноженный на 6
второй;
.
Из первого столбца вычтем удвоенный
второй, а из третьего - умноженный на 6
второй;
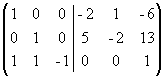 .
Прибавим третий столбец к первому и
второму:
.
Прибавим третий столбец к первому и
второму:
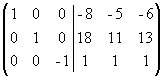 .
Умножим последний столбец на -1:
.
Умножим последний столбец на -1:
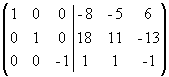 .
Полученная справа от вертикальной черты
квадратная матрица является обратной
к данной матрице А. Итак,
.
Полученная справа от вертикальной черты
квадратная матрица является обратной
к данной матрице А. Итак,
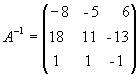 .
.
Вводные замечания. Одним из способов решения систем линейных алгебраических уравнений является правило Крамера, согласно которому каждое неизвестное представляется в виде отношения определителей:
![]() ,
,
где
![]() – определитель матрицы, получающейся
из матрицы А
заменой i-го
столбца столбцом правых частей системы
(3.1). Определители при этом предлагается
вычислять по формулам, рассматриваемым
в курсах линейной алгебры, например
– определитель матрицы, получающейся
из матрицы А
заменой i-го
столбца столбцом правых частей системы
(3.1). Определители при этом предлагается
вычислять по формулам, рассматриваемым
в курсах линейной алгебры, например
![]() .
(3.8)
.
(3.8)
Здесь
индексы ,
,
…,
пробегают все возможные
![]() перестановок номеров
перестановок номеров
![]() ;
k
– число инверсий в данной перестановке.
;
k
– число инверсий в данной перестановке.
Однако
в качестве конкретного метода решения
системы (3.1) данные формулы совершенно
неприменимы, так как при подсчете каждого
определителя по приведенной выше формуле
надо вычислить
![]() слагаемых, что нереально при весьма
умеренных значениях n.
Например, уже при
слагаемых, что нереально при весьма
умеренных значениях n.
Например, уже при
![]() имеем
имеем
![]() .
.
Очевидно, что сложность системы (3.1) определяется структурой ее матрицы А. Существуют два случая, когда система имеет простые решения. Если А – диагональная матрица
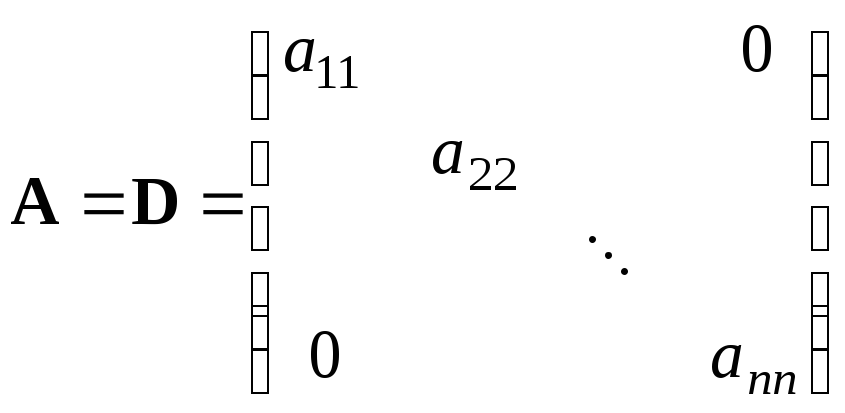 ,
,
то система (3.1) распадается на n независимый уравнений, каждое их которых содержит одну неизвестную величину, и проблем с вычислениями не возникает.
Просто решается задача и в случае, когда матрица А является треугольной
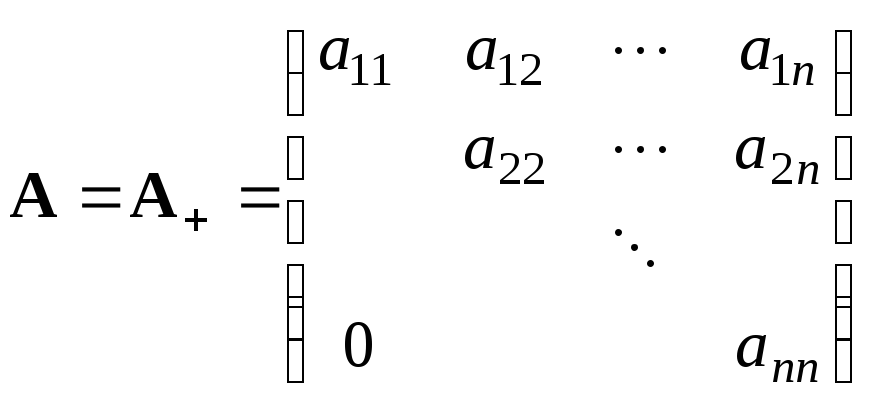 .
.
В этом случае из последнего уравнения следует
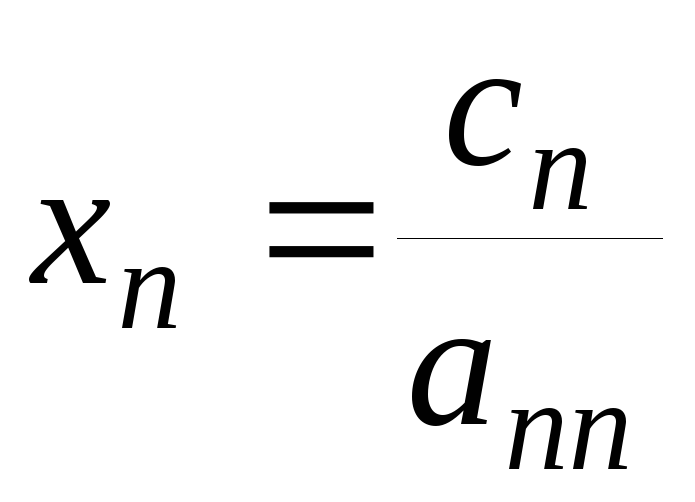 ,
,
и далее
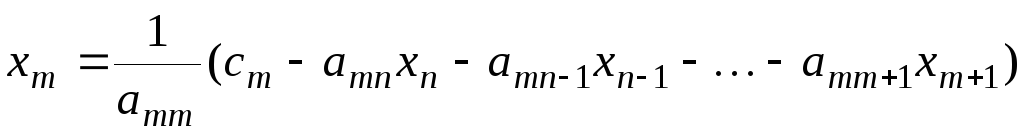 ,
,
для
![]() .
.
Оценим
объем вычислений, связанный с решением
системы с треугольной матрицей. Для
того, чтобы вычислить
![]() требуется одна операция, для вычисления
требуется одна операция, для вычисления
![]() – три,
– три,
![]() – пять и т.д. Как можно подсчитать, общее
число операций при этом равно
– пять и т.д. Как можно подсчитать, общее
число операций при этом равно
![]() .
.
Большинство прямых методов решения системы (3.1), используемых на практике, основаны на приведении исходной матрицы к треугольному виду с последующим нахождением неизвестных по рассмотренным выше формулам. Одним из таких методов является метод исключения Гаусса. Другие методы созданы специально для систем, обладающих матрицей определенного вида, например трехдиагональной матрицей. К таким методом относится метод прогонки. Ниже подробно рассматриваются оба этих метода.
Метод Гаусса. Метод исключения Гаусса содержит два этапа: прямой ход – приведение исходной матрицы к треугольному виду путем последовательного исключения неизвестных из уравнений системы и обратный ход – решение системы с треугольной матрицей. Рассмотрим одну из возможных реализаций прямого хода.
Пусть
![]() .
Тогда этот элемент называется ведущим
или главным.
Введем обозначение
.
Тогда этот элемент называется ведущим
или главным.
Введем обозначение
![]() ,
,
![]() .
.
Вычтем
последовательно из второго, третьего,
…, n-го уравнения
системы (3.1) первое уравнение, умноженное
соответственно на
![]() ,
,
![]() ,
…,
,
…,
![]() .
Это позволит обратить в нуль коэффициенты
при
.
Это позволит обратить в нуль коэффициенты
при
![]() во всех уравнениях, кроме первого. В
результате получим эквивалентную
систему в виде
во всех уравнениях, кроме первого. В
результате получим эквивалентную
систему в виде
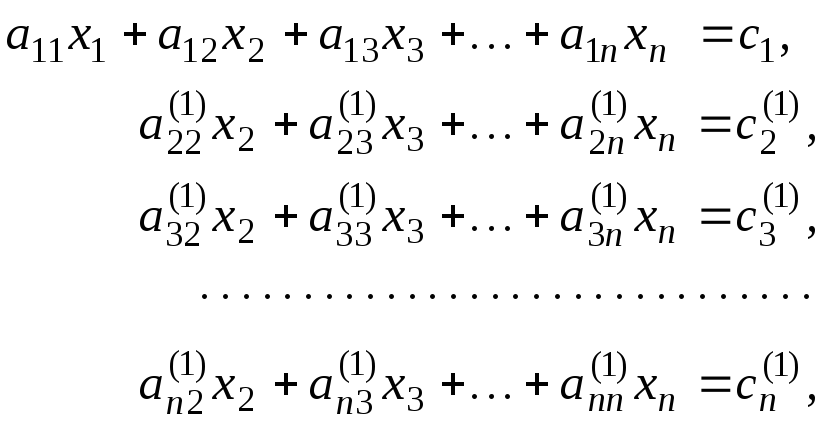 (3.9)
(3.9)
где
![]() ,
,
![]() ;
;
![]() .
.
Теперь
исключим неизвестное
![]() из уравнений, начиная с третьего. Пусть
из уравнений, начиная с третьего. Пусть
![]() – новый ведущий элемент; положим снова
– новый ведущий элемент; положим снова
![]() ,
,
![]() и вычтем из третьего, четвертого, …,
n-го уравнения второе
уравнение, умноженное соответственно
на
и вычтем из третьего, четвертого, …,
n-го уравнения второе
уравнение, умноженное соответственно
на
![]() ,
,
![]() ,
…,
,
…,
![]() .
В результате получим
.
В результате получим
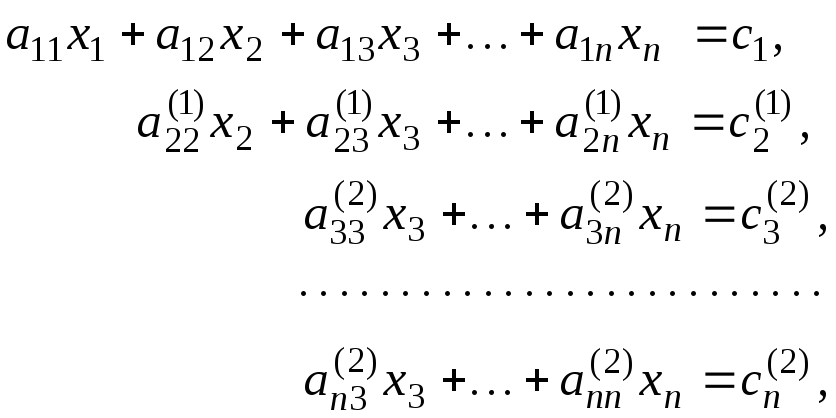 (3.10)
(3.10)
где
![]() ,
,
![]() ;
;
![]() .
.
Проделывая
описанные действия
![]() раз получим систему уравнений с
треугольной матрицей
раз получим систему уравнений с
треугольной матрицей
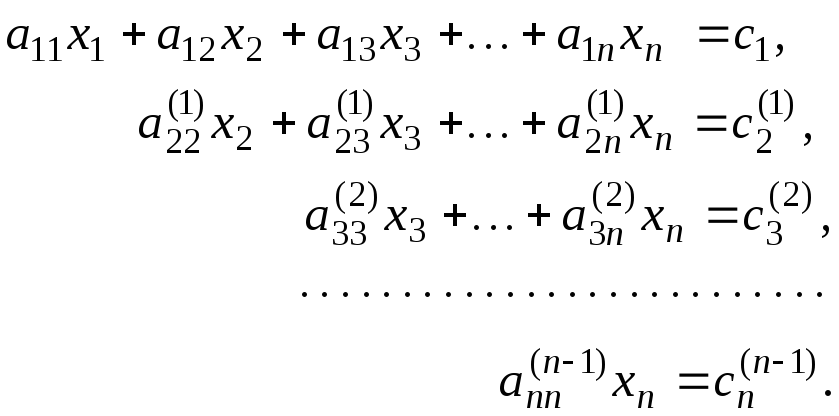 (3.11)
(3.11)
На
этом завершается прямой ход метода
Гаусса. Общее количество арифметических
операций, которые необходимо совершить
для приведения системы к треугольному
виду описанным методом, оценивается
величиной ![]() .
Это вполне приемлемая величина (при n
.
Это вполне приемлемая величина (при n
![]() и быстродействии ЭВМ порядка
и быстродействии ЭВМ порядка
![]() операций в секунду требуемое для расчета
время порядка одного часа).
операций в секунду требуемое для расчета
время порядка одного часа).
Замечание.
В процессе исключения неизвестных
приходится выполнять операции деления
на коэффициенты
![]() ,
,
![]() и т.д. Поэтому они должны быть отличны
от нуля. В противном случае необходимо
соответственным образом переставить
уравнения системы. Перестановка уравнений
должна быть предусмотрена в вычислительном
алгоритме при его реализации на
компьютере.
и т.д. Поэтому они должны быть отличны
от нуля. В противном случае необходимо
соответственным образом переставить
уравнения системы. Перестановка уравнений
должна быть предусмотрена в вычислительном
алгоритме при его реализации на
компьютере.
Обратный ход начинается с решения последнего уравнения системы (3.11):
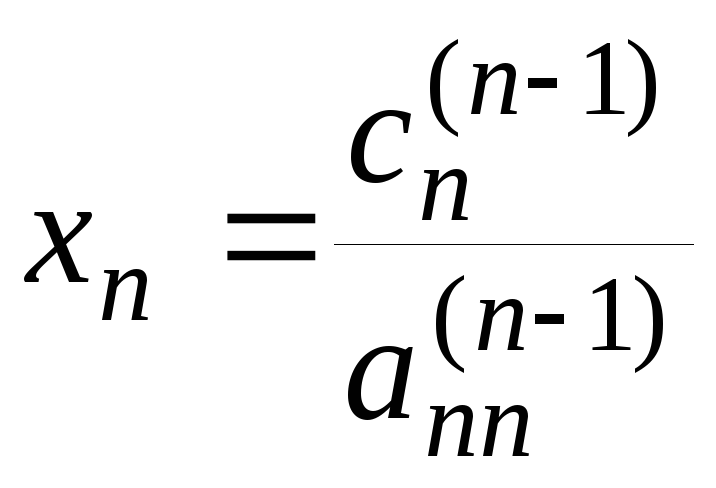 ,
,
затем
из предпоследнего уравнения находится
![]() :
:
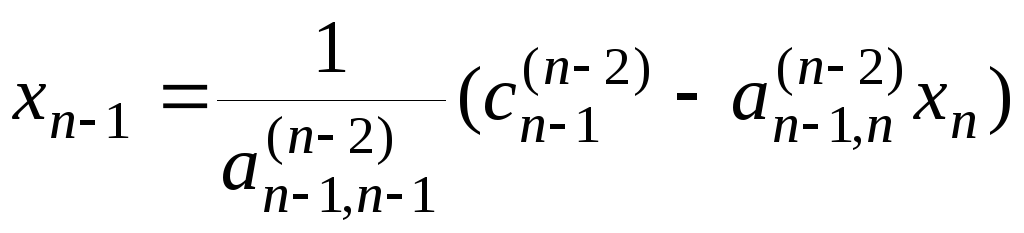 ,
,
аналогично определяются и все остальные неизвестные.
Ниже приведено описание вычислительного алгоритма метода Гаусса.
-
Ввод n,
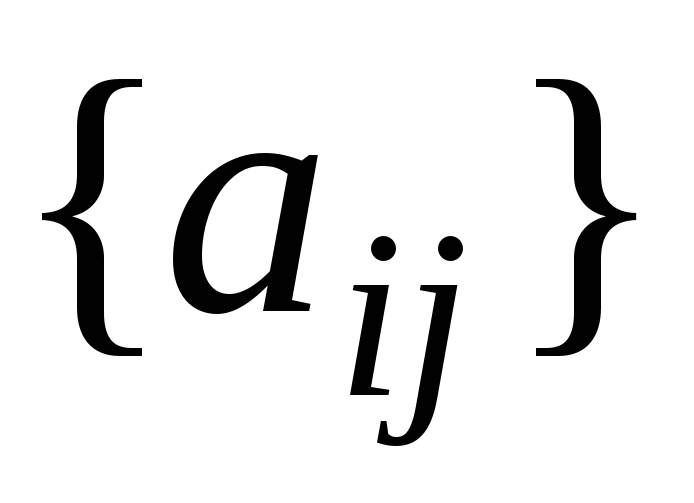 ,
,
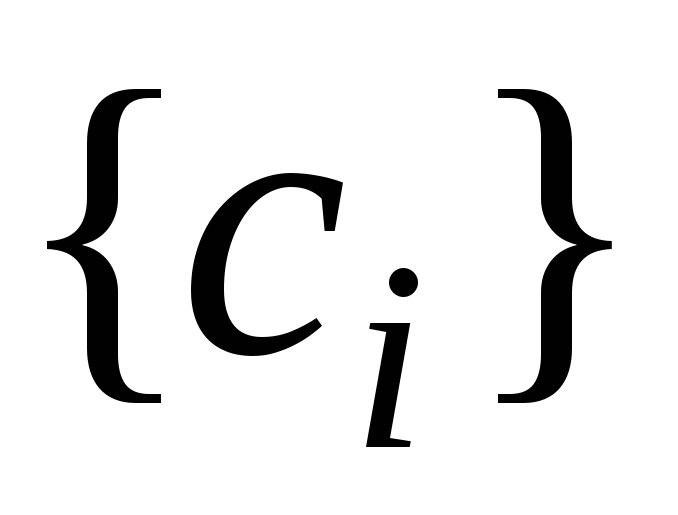
-
Для i от 1 до
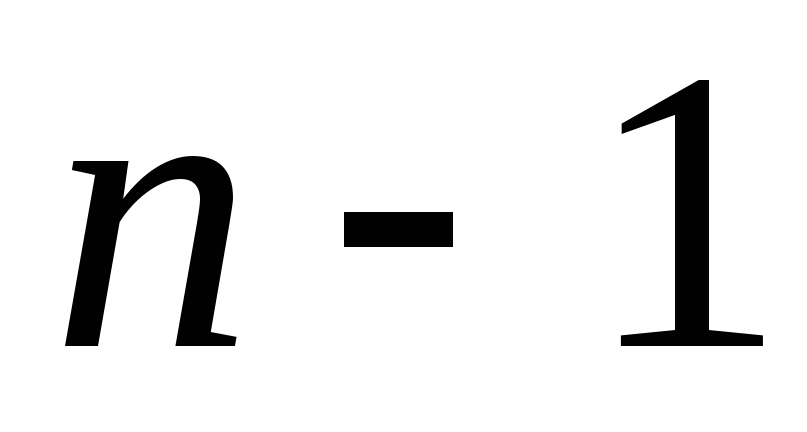 :
:-
Если
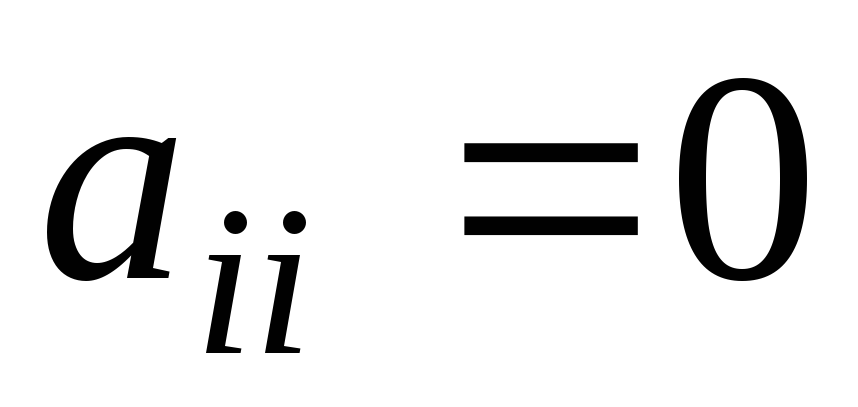 ,
тогда Перестановка
уравнений
,
тогда Перестановка
уравнений -
Для k от
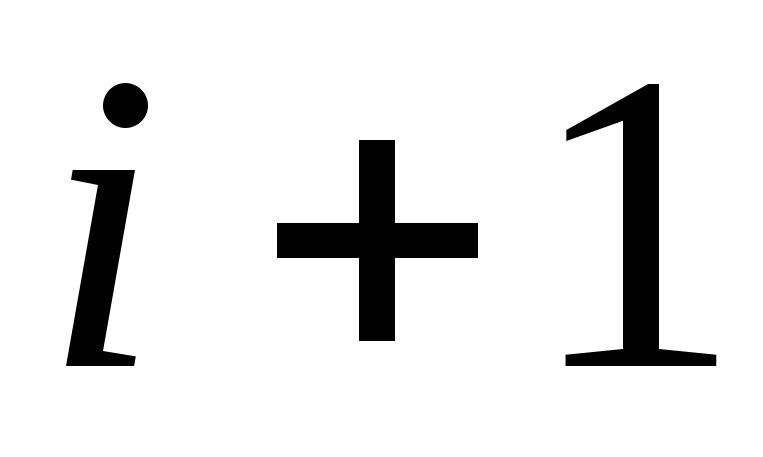 до n :
до n :-
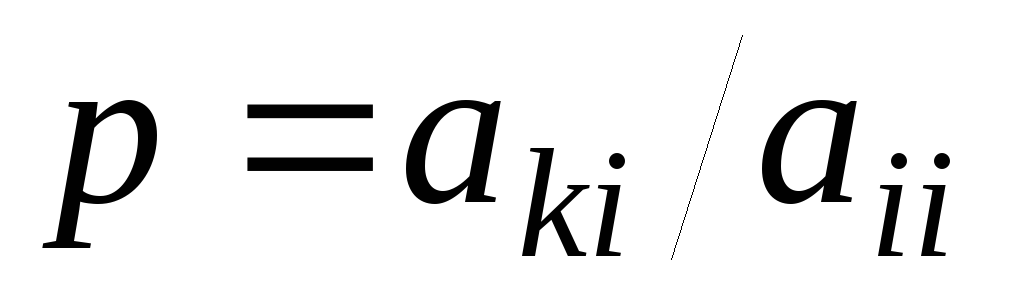
-
Для j от
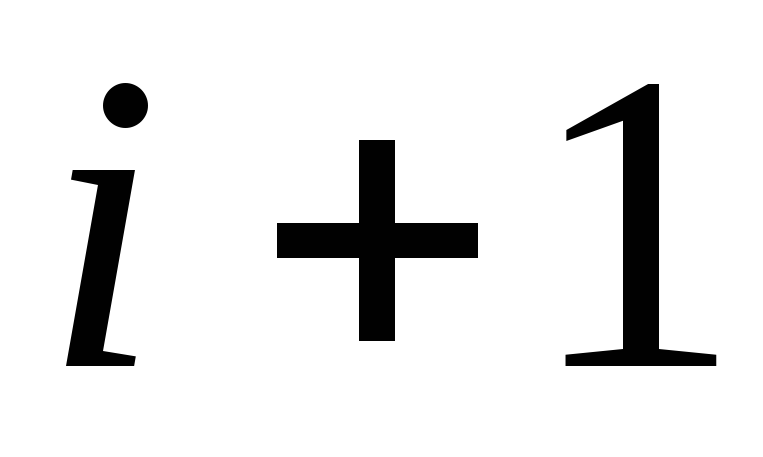 до n :
до n :
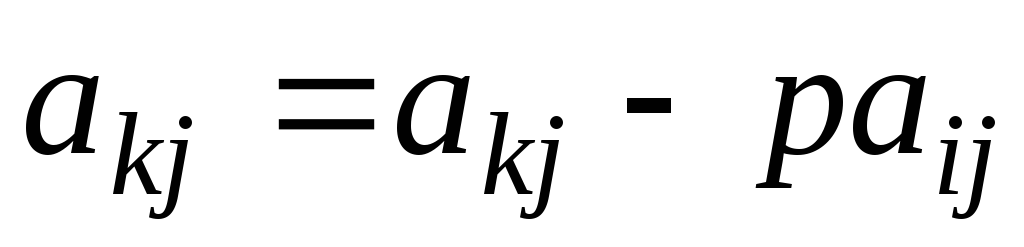
-
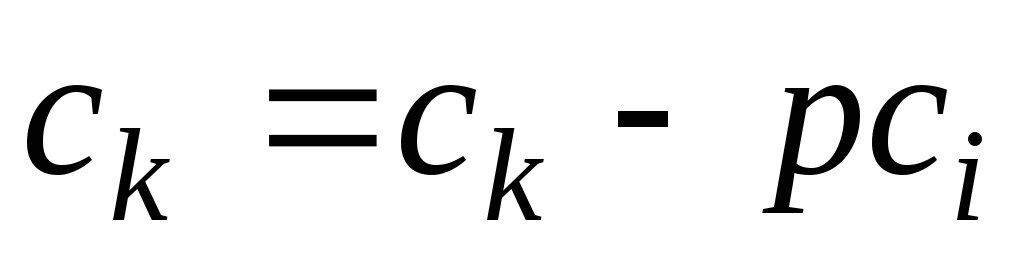
-
-
-
Для i от n до 1 с шагом –1 :
-
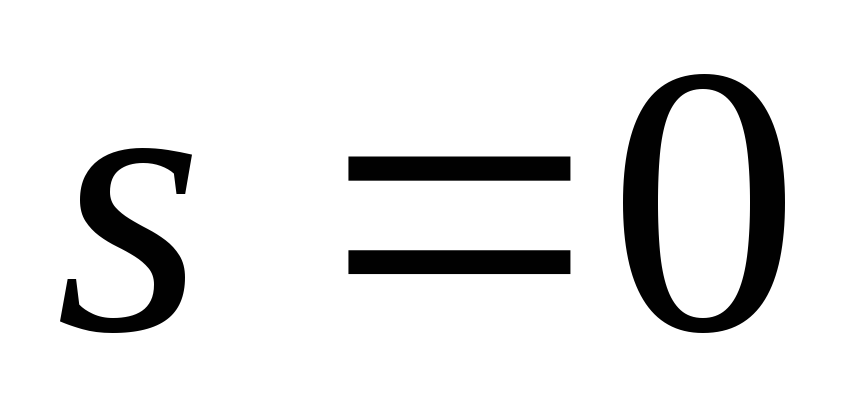
-
Для j от
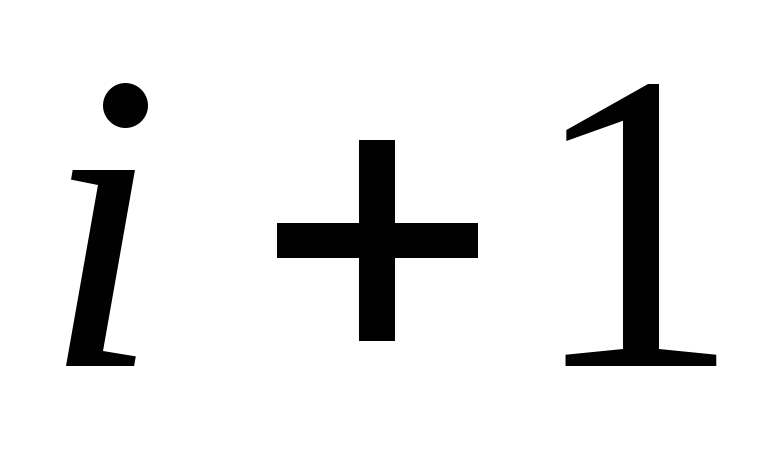 до n :
до n :
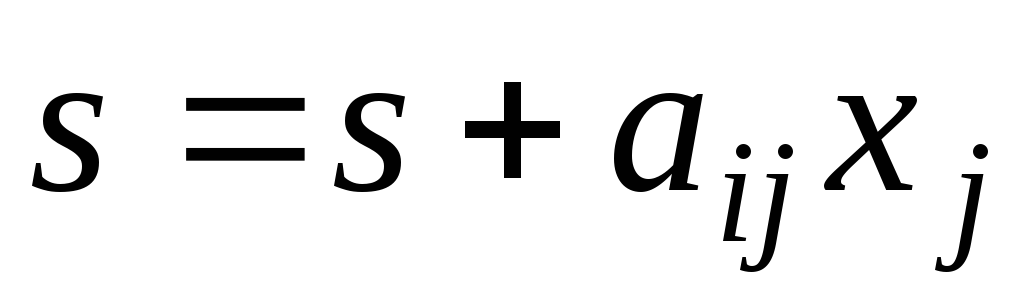
-
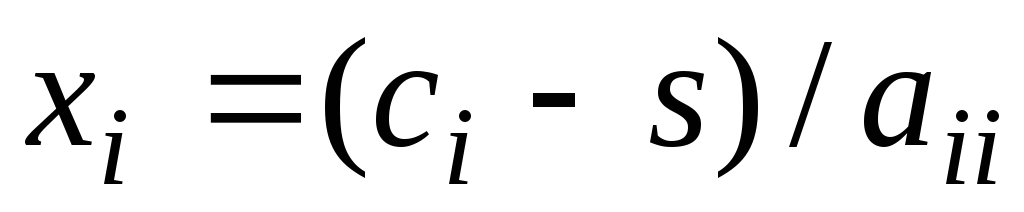
-
-
Вывод
В приведенном алгоритме первый цикл с параметром i реализует прямой ход, а второй – обратный ход метода Гаусса.
Одной
из модификаций метода Гаусса является
схема с выбором главного
элемента. Она состоит
в том, что требование неравенства нулю
диагональных элементов
![]() ,
на которые происходит деление, заменяется
более жестким: из всех оставшихся в i-м
столбце элементов нужно выбрать
наибольший по модулю и переставить
уравнения так, чтобы этот элемент
оказался на месте элемента
,
на которые происходит деление, заменяется
более жестким: из всех оставшихся в i-м
столбце элементов нужно выбрать
наибольший по модулю и переставить
уравнения так, чтобы этот элемент
оказался на месте элемента
![]() .
Это так называемый выбор главного
элемента по столбцу.
Существуют также схемы с выбором главного
элемента по строке
и по всей матрице.
.
Это так называемый выбор главного
элемента по столбцу.
Существуют также схемы с выбором главного
элемента по строке
и по всей матрице.
Алгоритм выбора наибольшего элемента по столбцу достаточно прост и состоит из двух этапов: отыскание номера наибольшего элемента и перестановки элементов двух строк. Описание алгоритма приведено ниже.
-
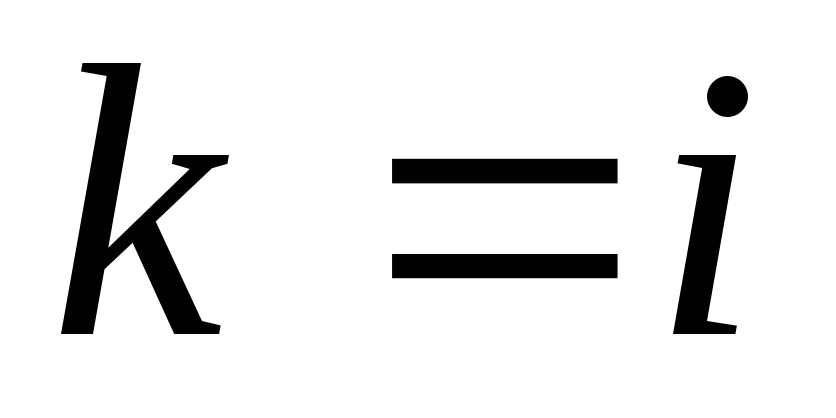
-
Для m от
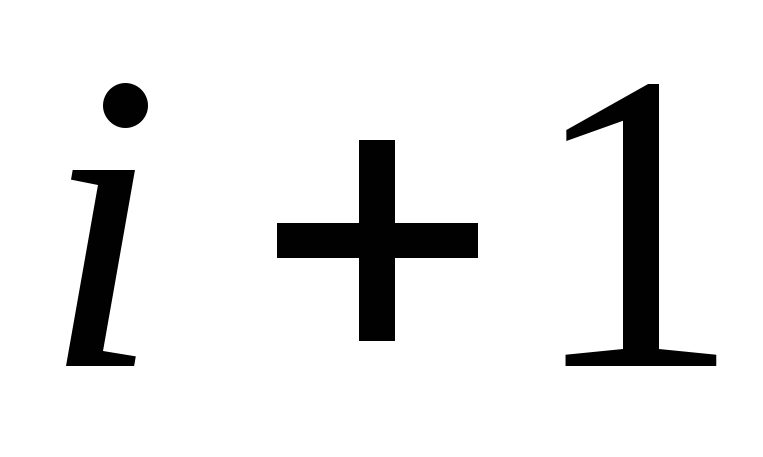 до n :
до n :-
Если
 ,
тогда
,
тогда
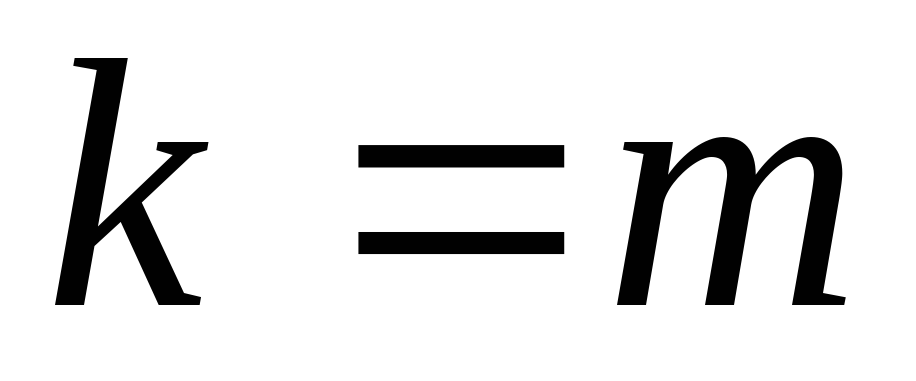
-
-
Если
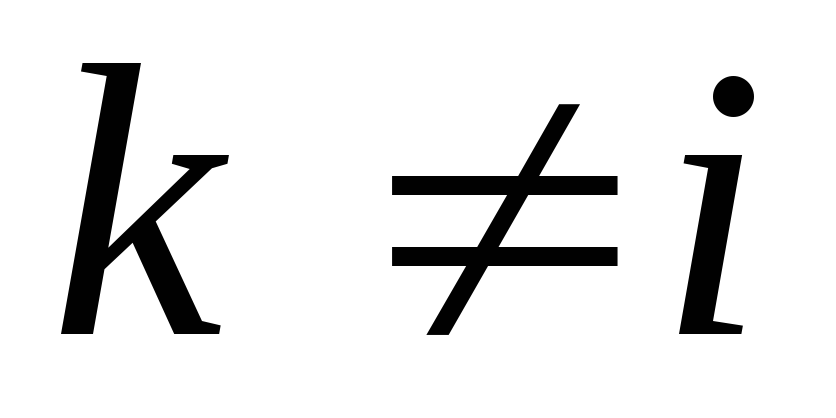 ,
тогда
,
тогда-
Для j от i до n :

-

-
Здесь
k – номер наибольшего
по абсолютной величине элемента матрицы
в столбце с номером i.
Этот алгоритм встраивается в приведенный
выше алгоритм метода Гаусса вместо
условной конструкции, выполняющей
перестановку уравнений в случае равенства
нулю элемента
![]() (шаг 2.1.).
(шаг 2.1.).
Благодаря выбору наибольшего по модулю ведущего элемента уменьшаются множители, используемые для преобразования уравнений, а также снижается вероятность деления на малые числа, что в итоге способствует уменьшению вычислительных погрешностей.
