5.5. Лінії другого порядку. Загальні рівняння.

Загальне рівняння лінії другого порядку має вигляд

,

де коефіцієнти А, В, С, D, E, F – будь-які числа, крім того, числа А, В, С не дорівнюють нулю одночасно. В залежності від знаку величини лінії другого порядку поділяються на три типа:

1. еліптичний, якщо >0;

2. гіперболічний, якщо <0;

3. параболічний, якщо =0.

Розглянемо лінії другого порядку різних типів: коло, еліпс, гіпербола, парабола.

5.8. Канонічні рівняння кола та еліпса

Колом називається множина точок, відстань кожної з яких до однієї точки, що називається центром, є величина стала. Відстань будь-якої точки кола від її центра – це радіус кола.

Знайдемо рівняння кола з центром у точці та радіусом R. Нехай – деяка точка кола. Тоді з визначення маємо (рис.5.5) , або , або

.

Це буде шукане рівняння кола. Якщо центр кола співпадає з початком координат, то рівняння кола буде:

.

Еліпсом називається множина точок, сума відстаней яких від двох фіксованих точок площини, що називаються фокусами, є величина стала.

Для знаходження канонічного рівняння еліпса позначимо – довільну точку еліпса. Нехай вісь Оx проходить між фокусами, а вісь Oy – через середину відстані між фокусами. Тоді з визначення еліпса (рис.5.6). відстань між фокусами нехай буде дорівнювати 2с (2а>2с), тобто для еліпса а>с.

Рис.5.5 Рис.5.6

Запишемо рівняння еліпса відповідно до його визначення:

.

Спростимо одержане рівняння

.

Позначимо через величину . Одержимо

,

або

.

Це рівняння називається канонічним рівнянням еліпса.

Таким чином, еліпс – замкнута крива, яка симетрична відносно вісей координат та початку координат, тому що разом з точкою до цієї кривої належать і точки , , . Усі точки еліпса лежать у середині прямокутника, який обмежений прямими . Точки та називаються вершинами еліпса, а числа та – піввісями еліпса. Для еліпса . Величина називається ексцентриситетом еліпса та характеризує його форму. Якщо , то (еліпс переходить в коло), якщо зменшувати , залишивши сталою, то еліпс буде наближатися до відрізка .

Ексцентриситет еліпса можна знайти за формулою:

або

, .

Лінії називаються директрисами еліпса .

Приклад. Задано еліпс: . Визначити його вісі, вершини, фокуси, директриси.

Розв’язання. Запишемо задане рівняння в канонічній формі:

.

Видно, що , . Тобто вісі: , . Координати вершин еліпса : (3; 0), (-3;0), (0; 2), (0; -2). Знайдемо величину . Таким чином, , . Для рівнянь директрис еліпса знаходимо ексцентриситет . Тоді маємо: .

5.9. Канонічне рівняння гіперболи. Асимптоти гіперболи.

Гіперболою називається множина точок, для яких різниця відстаней від двох фіксованих точок площини, що називаються фокусами, є величина стала.

Якщо точка належить гіперболі, а та – її фокуси, то властивість точок гіперболи можна записати: . Канонічне рівняння гіперболи буде:

,

де

.

Гіпербола, як еліпс, симетрична відносно вісей координат (рівняння парного ступеня). Усі точки гіперболи лежать поза смугою, обмеженою прямими . Точки називаються вершинами гіперболи; – дійсна піввісь, – уявна піввісь.

Розв’яжемо рівняння гіперболи відносно :

.

Якщо ; , гіпербола має нескінченні гілки та, крім того, при великих значеннях змінна буде наближатися до , а це означає, що гіпербола буде наближатися до прямих . Дійсно

.

Прямі називаються асимптотами гіперболи. Внаслідок того, що , точки гіперболи лежать у середині кута, який утворенo асимптотами (рис.5.7).

Рис.5.7 Рис.5.8

Позначимо – ексцентриситет гіперболи. Якщо  збільшується, a – фіксовано, то зростає і b, тобто збільшується кут між асимптотами. При гіпербола наближається до відрізків та осі Оx. Точку перетину асимптот гіперболи називають центром гіперболи. Поряд з гіперболою можна розглянути гіперболу . Її дійсна вісь – це вісь Oy, асимптоти співпадають з асимптотами початкової гіперболи. Ці гіперболи називаються спряженими (рис.5.8).

Якщо піввісі гіперболи рівні одна одній, тобто , гіпербола називається рівнобічною. Рівняння її асимптот , тобто вони взаємно перпендикулярні. Така гіпербола задається рівнянням .

Ексцентриситет гіперболи можна знайти за формулою:

,

або

.

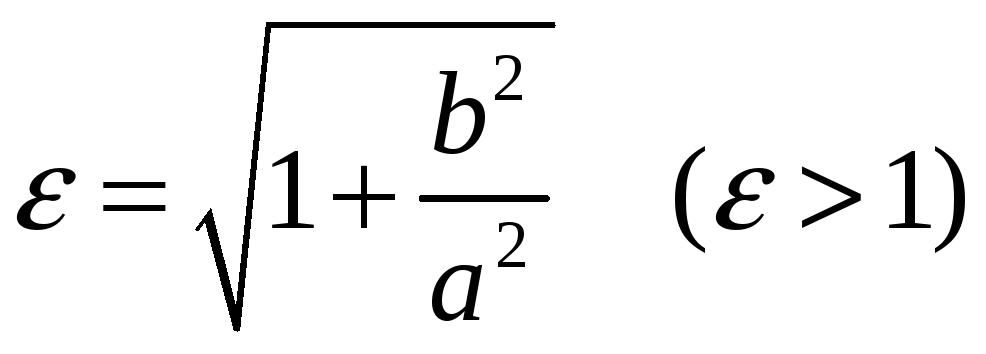Ексцентриситет характеризує форму прямокутника, діагоналями якого є асимптоти гіперболи. Для гіперболи (рис.5.7) рівняння директрис , для спряженої гіперболи (рис.5.8) рівняння директрис .

Приклад. Задано гіперболу: . Знайти її вісі, вершини і фокуси, асимптоти, директриси.

Розв’язання. Запишемо задане рівняння в канонічній формі . Бачимо, що , и . Тобто вісі гіперболи: , . Координати вершин гіперболи: (4; 0), (-4; 0). Знайдемо величину . Маємо координати фокусів: (5;0), (-5;0).

Рівняння асимптот: . Визначимо величину : . Отже, рівняння директрис: .