5.4. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої у відрізках на осях

Якщо дві точки та належать прмій, то напрямним вектором прямої буде вектор , тобто

.

Тоді рівняння прямої, що проходить через дві точки, має такий вигляд:

; ; .

Запишемо рівняння прямої у відрізках на осях. Нехай пряма перетинає осі та відповідно у точках , . Рівняння прямої, що проходить через ці точки, буде:

.

Це рівняння є рівнянням прямої у відрізках на осях.

Приклад. Трикутник задано його вершинами , , .

Знайти рівняння сторін трикутника. Рівняння прямої, що проходить через дві точки та буде:

,

або

.

Аналогічно можна знайти рівняння інших сторін.

5.5. Взаємне розміщення двох прямих на площині

Нехай на площині задано дві прямі з нормальними векторами ; :

1) ()

2) ().

Якщо , тоді та , тобто при

.

При маємо та

.

Кут між двома прямими дорівнює куту між та :

.

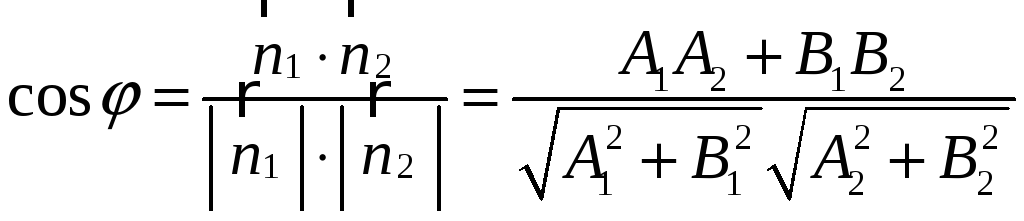Нехай прямі задані рівняннями з кутовими коефіцієнтами:

1) ()

2) ()

тоді

,

де , ; .

.

При маємо , тобто .

При маємо .

Приклад. Для трикутника записати рівняння перпендикулярів, що проходять через середини сторін, знайти координати центра описаного кола,за умови попереднього прикладу.

1. Середина сторони буде мати координати

; ,

тобто .

2. Через точку 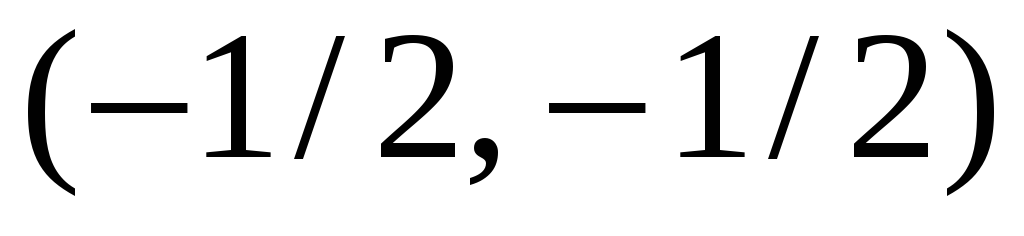треба провести пряму, перпендикулярну до прямої . Кутовий коефіцієнт прямої ; . Тоді кутовий коефіцієнт серединного перпендикуляра k=-7/5

3. Рівняння прямої, перпендикулярної , яка проходить через точку , буде:

,

або

,

або

Аналогічно знайдемо рівняння прямої, перпендикулярної , що проходить через середину відрізка . Таким рівнянням буде: .

4.Знайдемо точку перетину двох прямих:

.

Таким чином, координати центра описаного кола будуть:

; .

5.6. Нормальне рівняння прямої на площині, відстань від точки до прямої

Нехай за нормальний вектор прямої (рис.5.2) вибрано одиничний вектор та задана відстань від початку координат до прямої. Знайдемо проекцію вектора , який проведено від початку координат, до будь-якої точки прямої на вектор .

Рис.5.2 Рис.5.3

Отже, . Відзначимо, що , та запишемо нормальне рівняння прямої у векторній формі:

,

або у скалярній:

.

Це рівняння має дві важливі властивості:

1) ;

2) .

На основі цих властивостей можна загальне рівняння прямої привести до нормального вигляду. Помножимо загальне рівняння прямої на нормувальний множник

та знайдемо з умови:

; .

.

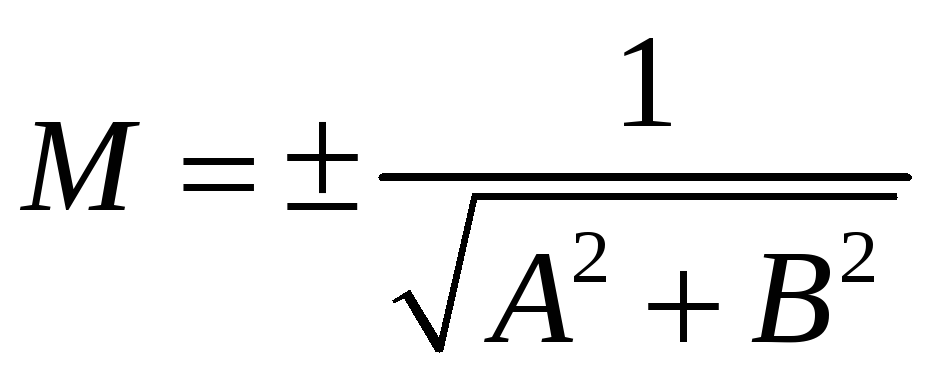Отже, щоб привести загальне рівняння прямої до нормального виду, слід поділити його на довжину нормального вектора, яка має знак протилежний знаку вільного члена.

Для знаходження відстані точки до прямої проведемо із точки вектор у будь-яку точку даної прямої (рис. 5.3). Отже,

,

або

.

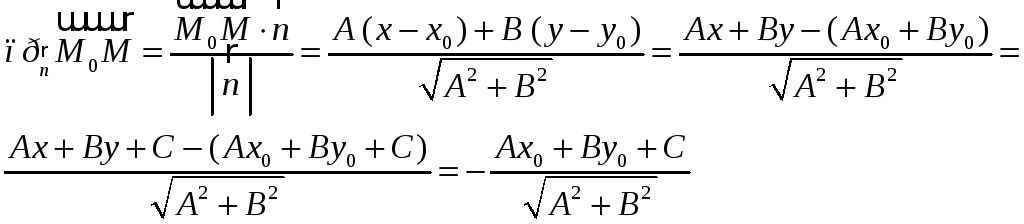(точка належить прямій, тому .) Звідси одержимо:

.

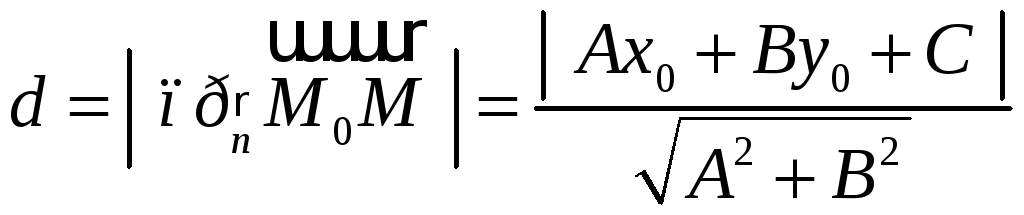Таким чином, щоб знайти відстань від точки до прямої, треба привести рівняння прямої до нормального виду, підставити в нього координати точки і даний вираз узяти по модулю.

Приклад. Задано трикутник з вершинами А(2; 1), В(3; 0), С(5; 4). З вершини А проведені висота, медіана, бісектриса. Скласти рівняння цих ліній і знайти їх довжину. Обчислити площу трикутника.

Розв’язання. Зробимо схематичний рисунок (рис.5.4), де АК – висота, АМ – медіана, AN – бісектриса.

Рівняння висоти. Висота АК вектору ВС, тобто вектор (5-3, 4-0)= (2,4) є нормальним вектором до АК, яка проходить через точку А.

Рис.5.4

Рівняння АК:

.

, після скорочення

.

Другий спосіб.

Рівняння висоти АК знайдемо як рівняння прямої, що проходить через точку А і має кутовий коефіцієнт :

або .

Кутовий коефіцієнт знайдемо з умови АК ВС, тобто . Коефіцієнт має значення . Отже, . Рівняння висоти АК: , або . Довжину висоти АК знайдемо за формулою відстані точки А від прямої ВС: , де загальне рівняння прямої ВС. Рівняння прямої, яка проходить через дві точки В і С: . Отже, маємо або . Тоді .

Рівняння медіани можна скласти як рівняння прямої АМ, яка проходить через дві точки А і М, причому координати точки М знаходимо за формулами:

, , або , .

Рівняння медіани АМ дістанемо у вигляді

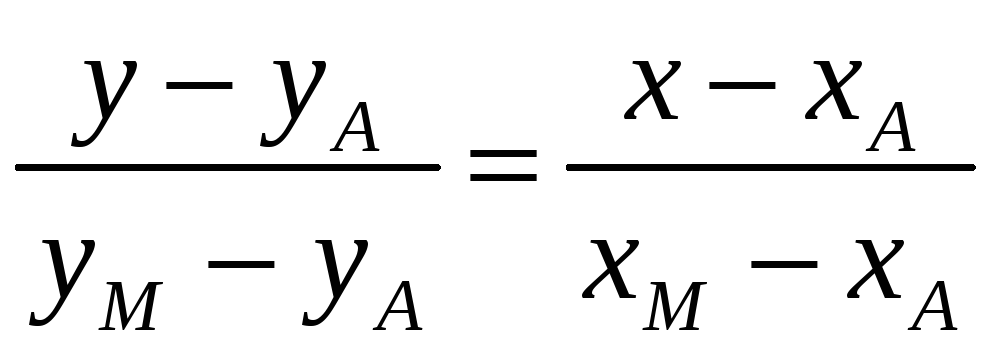, , або .

Довжину медіани знайдемо як відстань між двома точками:

,

.

Рівняння і довжину бісектриси AN можна знайти аналогічно рівнянню і довжині медіани АМ. Координати точки N дістанемо, скориставшись формулами

, ,

де – співвідношення, в якому точка N поділяє сторону ВС. Згідно із властивостями бісектриси трикутника . Довжину АВ і АС знаходимо як довжину між двома точками:

, .

Отже, і , .

Рівняння бісектриси:

, ,

або .

Довжина бісектриси

Площу трикутника обчислимо через модуль векторного добутку векторів і .

.