Розділ 3. Аналітична геометрія Лекція 5. Рівняння лінії на площині. Пряма та криві другого порядку

5.1. Поверхні та лінії у просторі. Їх рівняння. Геометричне тлумачення лінійного рівняння у двомірному та тримірному просторі.

5.2. Рівняння прямої, що проходить через задану точку. Загальне рівняння прямої та його дослідження.

5.3. Канонічне рівняння прямої. Рівняння прямої з кутовим коефіцієнтом.

5.4. Рівняння прямої, що проходить через дві задані точки. Рівняння прямої у відрізках на осях.

5.5. Взаємне розміщення двох прямих на площині.

5.6. Нормальне рівняння прямої на площині. Відстань від точки до прямої.

5.5. Лінії другого порядку. Загальне рівняння.

5.8. Канонічні рівняння кола та еліпса.

5.9.Канонічне рівняння гіперболи. Асимптоти гіперболи.

5.10. Парабола. Канонічне рівняння.

5.1. Поверхні та лінії у просторі. Їх рівняння

В аналітичній геометрії розв’язують дві основні задачі:

1. Множина точок задана геометричною властивістю. Знайти її рівняння та дослідити його властивості.

2. Дано рівняння. Дослідити множину точок, яка задається цим рівнянням.

Лінією у просторі називають лінію перетину двох поверхонь, тобто множину точок, координати яких задовольняют одночастно двом рівнянням:

.

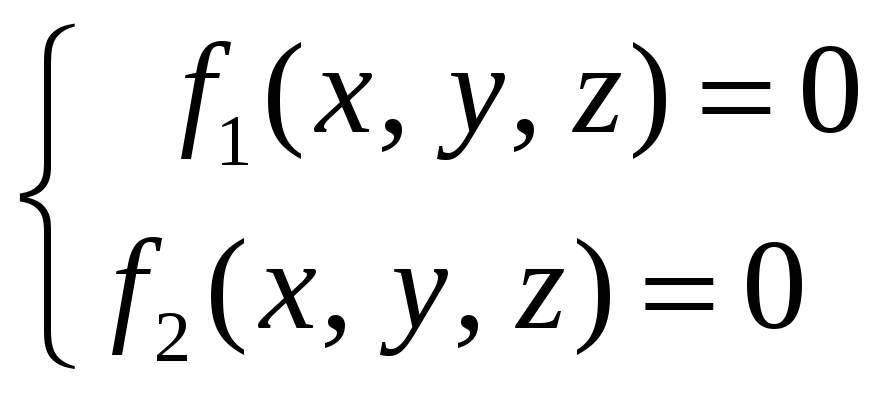Координати точок, що не лежать на лінії, не задовольняють систему рівнянь. У конкретному випадку:

.

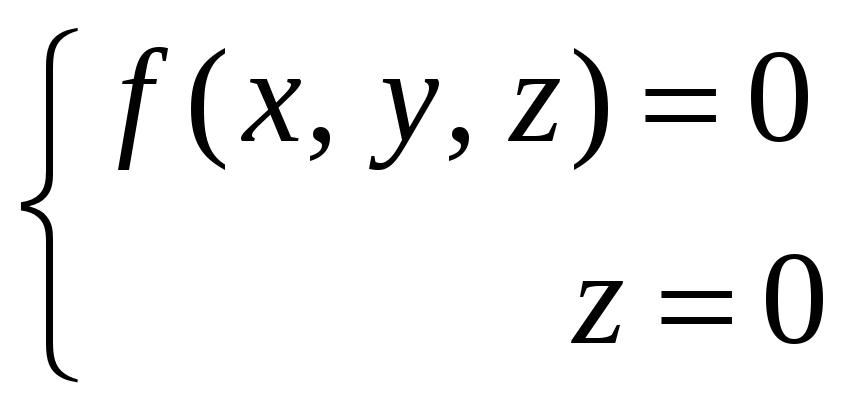Можна виключити з першого рівняння системи. У цьому випадку лінія належить площині , тобто - це рівняння лінії на площині.

Приклад. Знайти рівняння лінії, всі точки якої знаходяться на одній відстані від точки .

1. Вибираємо довільну точку на лінії.

2. Запишемо рівнянням умову задачі.

Відстань між точками та :

,

або

.

Це є рівняння кола, радіус якого дорівнює , а центр має координати .

5.2. Рівняння прямої, що проходить через задану точку. Загальне рівняння прямої та його дослідження

Пряма на площині визначається, якщо задати точку , яка належить даній прямій, та нормальний вектор , тобто вектор, який перпендикулярний до даної прямої (рис. 5.1).

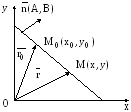
Рис. 5.1

Нехай - будь-яка точка, що належить даній прямій. Тоді, якщо точці відповідає радіус-вектор , а точці , то вектор з координатами . Вектори та взаємно- перпендикулярні, тому - векторне рівняння прямої, що проходить через точку . Або рівняння у скалярній формі

.

Розкриємо дужки, та позначимо , одержимо:

.

Це рівняння називається загальним рівнянням прямої на площині. Розміщення прямої на площині залежить від коефіцієнтів , і , .

1. , ; - пряма проходить через початок координат.

2. ; - пряма ; - паралельна осі , а якщо , одержимо рівняння осі .

3. ; - пряма ; - паралельна осі , а якщо , маємо рівняння осі .

Приклад. Записати рівняння прямої, що проходить через точку перпендикулярно вектору . На основі рівняння прямої одержимо:

,

або

.

5.3. Канонічне рівняння прямої, рівняння прямої з кутовим коефіцієнтом

Пряму на площині можна задати таким чином: задати точку та напрямний вектор , тобто вектор, який паралельний прямій. Візьмемо на прямій будь-яку точку (рис.5.1). Тоді вектор буде колінеарним вектору , або

(канонічне рівняння прямої).

Якщо напрямним вектором прямої вибрати одиничний вектор , то канонічне рівняння буде мати вигляд:

,

або

.

Позначимо . Тоді рівняння прямої , що проходить через дану точку, та утворює з віссю кут , буде:

.

Розв’язуючи це рівняння відносно , одержимо рівняння прямої:

.

Слід зауважити, що у цьому рівнянні - кутовий коефіцієнт, або тангенс кута нахилу прямої до осі ; - точка перетину з віссю . Одержане рівняння визначає будь-яку пряму площини, крім прямої, що паралельна осі .. А рівняння прямої, що проходить через точку , можна вважати рівнянням в’язки прямих, якщо у ньому - довільне.

Приклад . Записати рівняння прямої, що проходить через точку та утворює кут з віссю .

На основі рівняння одержимо:

,

або

.