Преобразования вещественных чисел в двоичной и десятичной системах счисления

Позиционная форма (2) вещественного числа содержит точку, разделяющую целую и дробную части числа. Целая часть переводится из одной системы счисления в другу по алгоритмам (3) - (5). Для образования дробной части используются позиционные порождающие единицы .1, .01, .001 и т.д. Чтобы выяснить соответствия в двоичной и десятичной системах, представим двоичное дробное число в виде суммы позиционных единиц с последующей подстановкой десятичных чисел на место двоичных чисел. Например,

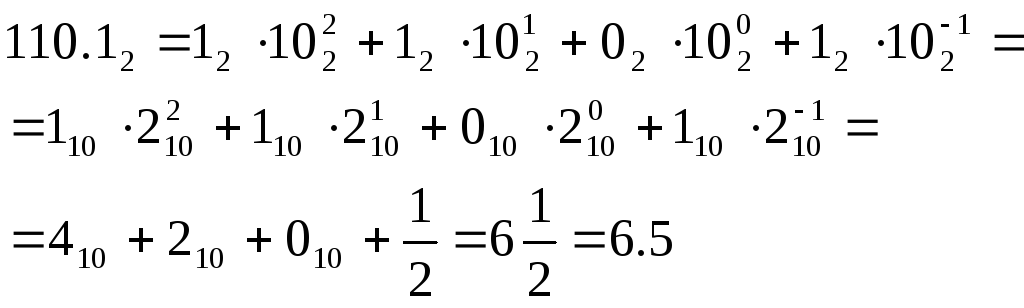(9)

Перевод дробного двоичного числа в десятичное число содержит две части:

1. перевод целой части;

2. перевод дробной части;

3. сложение переведенных целой и дробной частей.

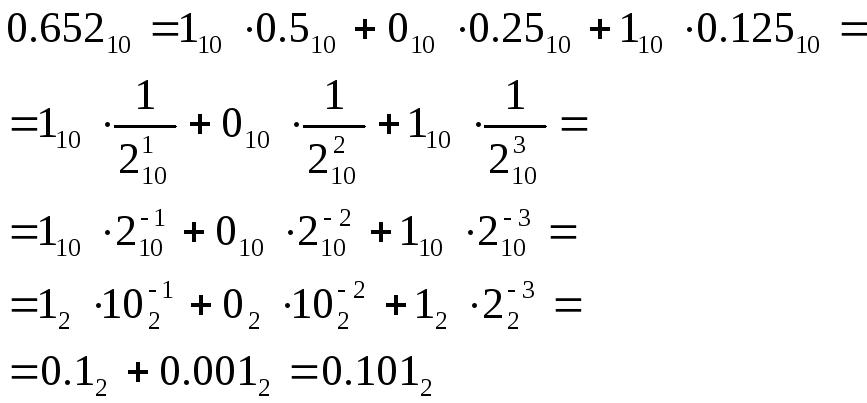(10)

Алгоритм перевода дробной части десятичного числа в двоичное число выглядит следующим образом:

1. представить десятичную дробь в виде суммы дробей степени 2;

2. заменить десятичные числа на двоичные числа;

3. выполнить арифметические действия с дробями в двоичной форме.

Ручной перевод использует операцию последовательного умножения исходной дроби и промежуточных результатов на число 2, отбрасывая получающуюся целую часть. Затем результат «собирается» в «прямом» порядке. Например, :

0.6875 0.375 0.75 0.5 0.0

2 2 2 2 2

1.3750 0.750 1.50 1.0 0.0

1 0 1 1

Нормальная форма вещественного числа

Если речь идет о произвольных вещественных числах, то в позиционной форме (2) количество цифр в целой и дробной частях может произвольно возрастать. Это становится ограничением для компьютерной реализации, поскольку процессор имеет фиксированное количество инструкций для выполнения операций над числами. Выход из создавшейся ситуации дает вариант нормальной формы представления числа X в виде мантиссы M и множителя-характеристики в системе счисления s. Число p называют порядком числа.

(10)

Поскольку в мантиссе отсутствует целая часть числа, то количество цифр может произвольно увеличиваться только в дробной части – это главное свойство нормализации. Окончательно принимают, что мантисса должна находиться в диапазоне . Следовательно, мантисса имеет следующую позиционную форму

, (11)

где n и m – количество цифр в целой и дробной частях числа в позиционной форме (2). Несколько примеров:

,

,

,

,

.

Нормализованные вещественные числа часто называют числами с плавающей точкой (запятой), поскольку реальный разделитель целой и дробной части в формате (2) перемещается в крайнюю левую позицию формата (11). Теперь процессор компьютера может иметь только несколько инструкций для выполнения арифметических действий над вещественными числами.

Четырехбайтовое представление вещественного числа в компьютере записывается по порядку: знак мантиссы, порядок, мантисса (рис.2). Кроме того, заметим, что мантисса двоичного числа всегда начинается с 1, за исключением числа 0. Следовательно, эту 1 можно не хранить, а лишь учитывать в арифметических инструкциях процессора. Так называемая спрятанная 1. Тогда мантисса может иметь длину на один бит больше, что является положительным фактором для округления чисел после выполнения вычислений и для вывода на монитор.

31	30	29	28	27	26	25	24	23	22	20	19	18	17	16	…	6	5	4	3	2	1	0
0	1	0	0	0	0	0	0	1	1	0	1	0	0	0	0	0	0	0	0	0	0	0

порядок мантисса

знак числа (мантиссы)

Рис. 2. Расположение числа +6.25 в 4-х байтах.

Порядок находится в битах 23 – 30. Для примера число +6.25. в двоичном нормализованном виде записывается как . Однако, на рис. 2 порядок записан не как 11₂ = 3₁₀, а как 10000001. Это сделано ради электронных схем процессора и имеет свой технический смысл, которого мы касаться не будем. Промежуточный порядок числа получается после прибавления 1 из бита 30 к числу в битах 23 – 29 :

1 0000001

+

0000001

1

0000010

Итак, промежуточный порядок 10₂ = 2₁₀. Можно рассуждать и другим способом, вычитая число из значения порядка

1

-

0000001

01111111

10

На втором этапе учитывается то, что за исключением числа 0 все остальные нормализованные двоичные мантиссы содержат 1 в первой дробной десятичной позиции. Следовательно, реальная мантисса получается их хранимой мантиссы путем приписывания спереди одной единицы. В нашем примере это выглядит так:

0.1001000…0 ~ 0.11001000…0

Тогда реальный порядок должен быть увеличен на 1 :

10₂ + 1₂ = 11₂ = 3₁₀

На третьем этапе получаем вещественное хранимое число с фиксированным расположением точки:

Ниже представлена программа C2 в которой функция BinaryFloat( ) выводит на монитор дает битовое изображение четырехбайтового вещественного числа типа float.

// Program C2

// Битовое изображение вещественного числа типа float

// Объединение union

#include <stdio.h> // printf

#include <conio.h> // getch

void BinaryFloat( char* text, float ff )

{ printf( "\n%s", text );// вывод текста на монитор

union

{ float f; вещественное представление

unsigned int n; // битовое представление

} u; // объект объединения

u.f = ff; // копирование в объект объединения

unsigned int b = 0x80000000; // 1 в бите 31

while( b > 0 ) // цикл бит

{ ( u.n & b ) == 0 ? printf( "0" ) : printf("1");

b >>= 1; // сдвиг 1 в соседний бит справа

}

}

//---------------------------------------------------

void main ( void )

{ float f; // 4-байтная вещественная переменная

printf( "f = " ); scanf( "%f", &f );//ввод числа

printf( "f = %f", f ); // монитор

BinaryFloat( "f = ", f ); // бинарный вид числа

getch(); // просмотр результата

}

Если при выполнении программы C2 ввести число 6.25, то следующие строки окажутся на мониторе. Двоичный вывод совпадает с рис. 2.

f = 6.25

f = 6.250000

f = 01000000110010000000000000000000

Функция BinaryFloat( ) создает двоичное изображение четырехбайтового вещественного числа и устроена по аналогии с функцией BinaryInt( ) (стр. 11). Конструкция объявления параметров содержит указатель char* text поясняющего текста и значение вещественного числа float ff. В теле функции BinaryFloat( ) текст выводится на монитор с новой строки printf( "\n%s", text ). Язык C++ не позволяет применять инструкции битовой логики к переменным типа float. Чтобы преодолеть ограничение, создадим объект u объединения union

union

{ float f; // вещественное представление

unsigned int n; // битовое представление

} u; // объект объединения

Смысл объединения состоит в том, что поля u.f и u.n занимают одни и те же 4 байта в оперативной памяти. Следовательно, в поле u.f можно загрузить вещественное число из параметра u.f = ff, а битовую логику выполнять над полем u.n. Дале алгоритм совпадает с инструкциями функции BinaryInt( ). Переменная unsigned int b = 0x80000000 содержит 1 в 31-ом бите. Битовое изображение на мониторе строится под управлением заголовка цикла while( b > 0 ). В теле цикла выполняется конъюнкция u.n & b над очередным битом вещественного числа с последующей распечаткой на мониторе ( u.n & b ) == 0 ? printf( "0" ) : printf( "1" ). На каждой итерации единица сдвигается вправо в переменной b >>= 1. Тело цикла завершено. Функция BinaryFloat( ) выполнена.