7.1. Послідовне складання паралельних сил. Центр пара­лельних сил

Припустимо, що до твердого тіла в точках А₁,А₂,...,А₅ при­кладені сили , з яких направлені в одну сторону, а - в протилежну (рис. 7.1). Додамо сили і за правилом додавання двох паралельних сил, направлених в один бік

Рис. 7.1

Визначивши модуль рівнодійної та її точку прикладення В₁, скла­демо і силу

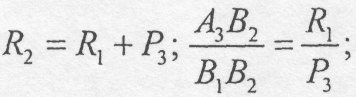
Аналогічно визначимо рівнодійну сил і

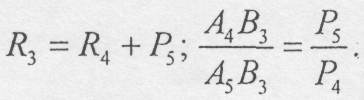
Внаслідок послідовного складання заданих паралельних сил одержимо дві протилежно направлені паралельні сили і в точках і . В залежності від модулів і точок прикладення цих сил можли­ві наступні випадки:

І. Сили і не рівні за модулем. Приймемо, що , тоді рівнодійна заданих сил має модуль і направлена в бік (рис 7.1). Точка прикладення рівнодійної С лежить на продов­женні відрізка В₂В₃ за точкою прикладення більшої сили , при чому 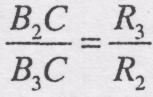. Точка С називається центром паралельних сил. Через цю точку обов'язково проходить лінія дії рівнодійної заданої системи сил, якщо, не змінюючи модуля сил, повертати лінії їхньої дії навколо точок прикладення сил на один і той самий кут, в один і той самий бік.

Дійсно, всі наведені рівності будуть і в цьому випадку справедливі.

II. Сили і рівні за модулем, але їх лінії дії не збігаються. В цьому випадку система зводиться до пари сил.

III. Сили і рівні за модулем і їх лінії дії збігаються. Задані сили в цьому випадку взаємно зрівноважуються. Система паралельних сил, направлених в один і той же бік не може врівноважуватись або при­водитись до пари сил. Ця система завжди має рівнодійну.

7.2 Формули радіуса-вектора і координат центра паралельних сил

Розглянемо систему паралельних сил , прикладених в точках А₁,А₂,...А_п, зведену до рівнодійної , прикладеної в точці С (рис. 7.2).

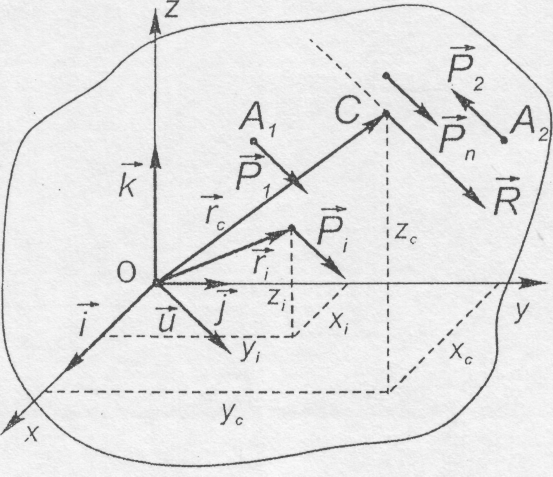
Рис. 7.2

Положення центра паралельних сил С визначається радіус-вектором відносно початку координат або координатами x_c, y_c, z_c. Положення точки прикладення кожної сили визнача­ється радіус-вектором , або координатами x_і, y_і, z_і, де .

За теоремою Варіньона про момент рівнодійної відносно будь-якого центра (див. 4.7), прирівнюємо момент рівнодійної відносно центра О геометричній сумі моментів складових сил відносно цього ж центра:

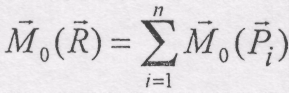або, згідно 3.1

Введемо одиничний вектор , паралельний лініям дії сил. Тоді , де - алгебраїчне значення сили, . Підставивши значення і у вирази моментів, будемо мати 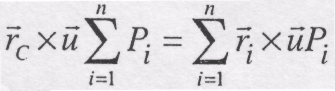. Перемістимо скалярні співмножники у век­торних добутках

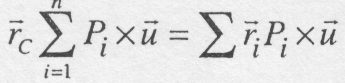, або

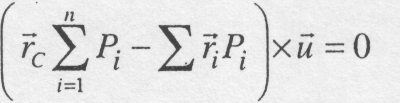
Вектор може мати будь-який напрямок, оскільки згідно властивості центра паралельних сил, лінії дії сил можна повертати. Отже,

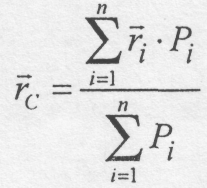^(7.1)

Спроектувавши ліву і праву частини (7.1) на осі координат, одержимо формули координат центра паралельних сил:

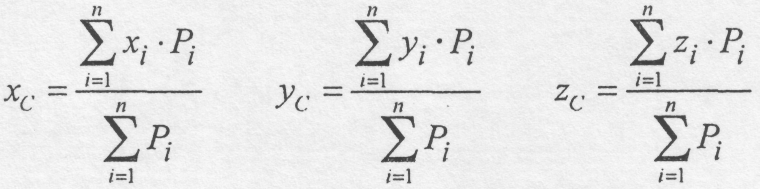^(7.2)

В формулах (7.2) чисельником і знаменником кожного дробу є алгебраїчні суми. Вибір напрямку, вздовж якого паралельні сили вважаються додатними - довільний і на результати обчислень не впли­ває.