8.4.2. Координатний спосіб визначення швидкості

Нехай, кінематичні залежності руху точки, задані координатним декартовим способом (8.2). Тоді формулу (8.18) можна записати так:

(8.19)

де (8.20)

Є проекції швидкості точки на осі нерухомої декартової системи координат, що дорівнюють першим похідним за часом від координат точки.

З урахуванням (8.20) вираз (8.19) можна записати у вигляді:

(8.21)

або

(8.22)

Рис. 8.12 Рис. 8.13

де v_x,v_y,v_z - складові вектора вздовж координатних осей (рис.8.12).

Модуль та напрям швидкості визначаються за формулами:

^(8.23)

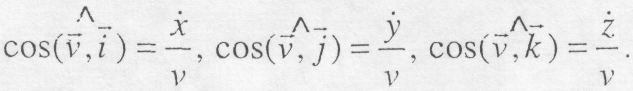^(8.24)

За рівностями (8.20) - (8.24) визначається вектор швидкості точки координатним декартовим способом.

Розглянемо координатний полярний спосіб визначення руху точки. При цьому кінематичні залежності руху точки задаються функ­ціями (8.9).

Введемо орти: , спрямований вздовж радіуса-вектора у бік зростання , та - повернений відносно вектора на кут у бік зростання кута φ (рис. 8.13).

Одиничні вектори і можуть бути подані у вигляді

Диференціюючи за часом, одержимо:

^(8.25)

аналогічно ^(8.26)

Радіус-вектор , що визначає положення точки, може бути представлений у вигляді

При русі точки змінюється як модуль, так і напрямок радіуса-вектора , отже, і і є функціями часу. На основі (8.18) маємо:

Використовуючи вираз (8.26), одержимо:

(8.27)

Це розкладання вектора швидкості точки на дві взаємно пер­пендикулярні складові, які називаються радіальною та поперечною (трансверсальною) швидкостями. Модуль швидкості точки визначається за формулою:

(8.28)

8.4.3. Натуральний спосіб визначення швидкості

Нехай точка М рухається по певній кривій. За проміжок часу ∆t точки переміститися з положення М в положення М₁ . Дуга MM₁ = ∆σ буде більше нуля, якщо точка рухається в сторону дода­тного відліку дуги (рис. 14,а) і , якщо рух проходить в протиле­жний бік (рис. 8.14,6).

Скориставшись виразами (8.14) і (8.18), маємо:

Перепишемо це рівняння у вигляді:

Рис. 8.14

Оскільки границя відношення дуги до стягуючої її хорди дорі­внює за модулем одиниці, а граничне положення січної ММ₁ співпа­дає з напрямком до дотичної до кривої в точці М , то

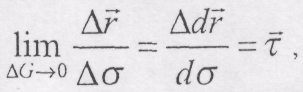
де - одиничний вектор, направлений по дотичній до кривої.

Направлений одиничний вектор дотичної завжди в сторо­ну додатного відліку дуги σ. Дійсно, якщо то вектор направлений в сторону (рис. 8.14.а), а при вектор направлений в сторону, протилежну (рис. 8.14,6). В обох випадках цей вектор, а отже і його границя , направлений в сторону зростання дуги σ.

Приймаючи до уваги, що

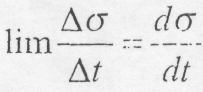маємо

Проектуючи вектор швидкості на напрям , одержимо

, отже

(8.29)

Очевидно, що v_𝜏 = v , якщо рух точки проходить в бік додат­ного відліку дуги і v_𝜏 = -v, якщо рух точки проходить в протилежну сторону, отже

Так як шлях, що проходить точка, завжди додатний, то елемент шляху

і, отже, модуль швидкості можна визначити за формулою: