1. Вычисление несобственных интегралов.

Леммы Жордано широко применяются при вычислении несобственных интегралов от экспоненциально растущих функций действительной и комплексной переменной. Мы рассмотрим лишь два типа интегралов. Первые касаются несобственных интегралов от функций, не имеющих особенностей на действительной оси, а вторые имеют прямое отношение к вычислению «оригиналов» в операционном исчислении, построенном на базе преобразования Лапласа.

1. Интегралы типа

Теорема 16.19. Пусть функция f(x), заданная на действительной оси – ∞ < x < ∞, может быть продолжена на верхнюю полуплоскость Im z ≥ 0 и ее аналитическое продолжение – функция f(z) – удовлетворяет условиям леммы Жордано в области Im z ≥ 0 и не имеет особых точек на действительной оси. Тогда несобственный интеграл (a > 0) существует и вычисляется по формуле

, (16.4)

где сумма берется по всем полюсам z_k, лежащим в верхней полуплоскости.

Доказательство. Пусть число R₀ таково, что все особые точки аналитического продолжения f(z) лежат внутри круга |z|< R₀ и R >  R₀. Рассмотрим замкнутый контур, состоящий из отрезка действительной оси R ≤ x ≤ R и дуги полуокружности. По основной теореме о вычетах

.

Здесь правая часть не зависит от R. Следовательно, при R ∞ существует предел левой части этого равенства. Переходя к пределу и воспользовавшись леммой Жордано, получим (16.4). Доказательство закончено.

Из (16.4) вытекают также следующие формулы.

, (16.5)

если f(x) – четная функция.

, (16.6)

если f(x) – нечетная функция.

Для доказательства этих равенств вначале заметим, что

=

=.

Отсюда равенство (16.5) следует, если предположить функцию f(x) четной, а равенство (16.6) – если предположить функцию f(x) нечетной.

Пример 16.1. Вычислить несобственный интеграл

Решение. Чтобы воспользоваться формулой (16.5) будем полагать a > 0, m > 0 и проверим выполнение условий леммы Жордано для аналитического продолжения функции. В самом деле, в верхней полуплоскости Re z ≥ 0 единственная особая точка z = i m является простым полюсом и на действительной оси функция f(z) не имеет особых точек. Кроме того, на окружности |z| = R ( R > R₀ = max(1,m)) выполняется равномерная относительно arg z оценка

.

Таким образом, выполнены условия леммы Жордано. По формуле (16.5) получим.

Нетрудно заметить, что по соображениям симметрии

.

2. Контур Бромвича и интеграл Бромвича – Вагнера.

Контуром Бромвича для функции Φ(z) комплексного переменного z называется прямая (с – i ∞, с + i ∞) (замкнутая бесконечно удаленной точкой) слева от которой находятся все особые точки функции Ф(z) (рис.8). Величина с, равная расстоянию от контура Бромвича до мнимой оси 0y всегда считается неотрицательной (с ≥ 0). Если все особые точки функции Φ(z) лежат левее оси 0y, то за контур Бромвича принимается ось 0y.

Рис. 8. Контур Бромвича. Замыкание слева.

Рис. 9. Контур Бромвича. Замыкание справа

Пусть для функции Ф(z) прямая Re z = с: (с – i ∞, с + i ∞) является контуром Бромвича. Следующий несобственный интеграл (при t > 0)

(16.7)

называется интегралом Бромвича – Вагнера.

Предположим, что функция Φ(z) удовлетворяет условиям леммы Жордано и воспользуемся леммой Жордано 16.4. Для этого выберем достаточно большое число R, чтобы все особые точки функции Φ(z) оказались внутри контура, составленного из отрезка и полуокружности C_R = {|z – c| = R , Re z < c}. Этот контур обозначим Γ. Всюду на контуре справедлива оценка. Поэтому условия леммы выполняются также и для функции. Согласно основной теореме о вычетах, имеем. С другой стороны,. Переходя к пределу при, получим

(t > 0). (16.8)

Условие t > 0 является важным для использования формулы (16.8). Рассмотрим, что будет, если это условие не выполняется. Приведенная выше оценка для функции примет вид на контуре Г. Если функция Φ(z) убывает как степенная функция, то все несобственные интегралы расходятся и формула (16.8) несправедлива. Однако, если замкнуть контур Г в правой полуплоскости (рис. 9), то для него условия леммы 16.4 выполняются и формула (16.8) примет вид , где суммирование производится по полюсам подынтегральной функции, находящимся внутри контура Г. Однако, по выбору контура Г, таких полюсов нет, внутри контура функция является аналитической, соответственно. Окончательно,

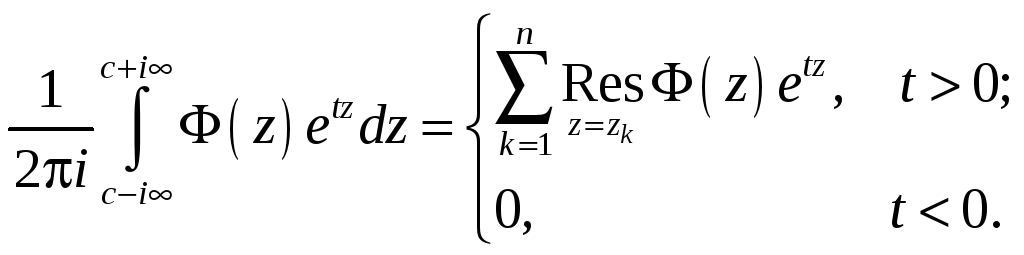(16.9)

В точке t = 0 интеграл вычисляется непосредственно.