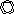Матрица перевозок с применением метода северо-западного угла

ai bj	30		100		40		110
60	4	30	5	30	2		3
100	1		3	70	6	30	2
120	6		2		7	10	4	110

На 1-м этапе определяем тип задачи и закрепляем потребителей за поставщиками (таблица 6.2 и 6.3).

a_i=60+100+120=280.

b_j=30+100+40+110=280.

a_i=b_j – закрытая транспортная задача.

В методе северо-западного угла первой заполняется клетка (1,1) по принципу x₁₁=min{a₁,b₁}, т.е. либо полностью удовлетворяется первый потребитель, либо полностью истощается первый поставщик, а затем остальные клетки 1-й строки: x₂=min{a₁-b₁,b₂} , если a₁>b₁ или переходит к заполнению соседней клетки (2,1), если a₁<b₁ и т.д.

После заполнения матрицы перевозок по методу северо-западного угла значение целевой функции будет:

f ()=430+530+370+630+710+4110=1170ед.

Недостатком метода является то, что он не учитывает значение элементов с_ij матрицы транспортных расходов и начальный опорный план перевозок далек от оптимального.

Метод наименьших стоимостей учитывает этот момент. Рассмотрим одну из модификаций метода – «двойное предпочтение», в соответствии с которым в первую очередь заполняются клетки с наименьшими значениями с_ij по строке и по столбцу (два кружка – отметины), затем клетки с наименьшими значениями или по строке, или по столбцу (один кружок – отметина).

Таблица 6.3

Матрица перевозок с применением метода наименьших стоимостей

bj ai	30			100			40			110			Ui
60	6			5			2	40	3		20	0
100	1	30	3			6			2		70	1
120	6			2	100	7			4		20	-1
Vj	2			1			2			3

Значение целевой функции значительно уменьшилось:

f ()=130+2100+240+270+320+420=590ед.

На 2-м этапе по методу потенциалов проверяем оптимальность плана. Рассмотрим процесс нахождения потенциалов для исходного плана по методу северо-западного угла. Зададимся значением U₁, т.к. одним значением U_i всегда можно задаться. Определяем по (6.5) для первой строки по заполненным клеточкам:

V₁=U₁+с₁₁ т.к. U₁=0 V₁= с₁₁; V₁=4.

V₂=U₁+ с ₁₂ V₂= с₁₂; V₂=5.

С другой стороны для второго столбца должно выполняться:

V₂=U₁+ с₁₂ и V₂=U₂+ с₂₂.

Но V₂=5, тогда U₂= V₂ – с₂₂ = 5 – 3 = 2.

Продолжая сравнение потенциалов по строке и столбцам, определяем все потенциалы (таблица 6.4).

Таблица 6.4

Потенциалы для метода северо-западного угла

bj ai	30		100		40		110		U1
60	4	30	5	30	2		3		0
100	1		3	70	6	30	2		2
120	6		2		7	10	4	110	1
Vj	4		5		8		5

В таблице 6.3 даны потенциалы для метода наименьших стоимостей. Чтобы оценить оптимальность распределения, для всех клеток (i, j) матрицы перевозок, определяют их оценки d_ij по формуле:

d_ij = (U_i+ с _ij) – V_j.

Об оптимальности плана судят по оценкам d_ij свободных клеток, т.к. оценки заполненных клеток равны нулю (цена потребителя покрывает цену поставщика и стоимость перевозок). Если оценка некоторой свободной клетки отрицательна, то это можно интерпретировать так: цена, предполагаемая соответствующим потребителем, больше суммы цены поставщика и стоимости перевозки, т.е. если бы эта клетка была занята, то можно было бы получить дополнительный экономический эффект. Т.о., условием оптимальности плана (распределения) служит условие неотрицательности оценок свободных клеток матрицы перевозок.

Оценки обычно представляются в виде матрицы оценок. Составим матрицу оценок для таблицы 6.4:

[d_ij]= .

Очевидно, что план далек от оптимального, т.к. большое число отрицательных оценок.

На 3-м этапе производим корректировку исходного плана. Выбирается клетка с наибольшей по абсолютной величине отрицательной оценкой, и строится прямоугольный контур, начальная вершина которого лежит в выбранной клетке, а все остальные вершины находятся в занятых клетках (d_ij=0). Вершинам контура присваиваются поочередно по контуру знаки «+», «–», начиная со знака «+» в выбранной свободной клетке.

Выбирается наименьшая величина поставок в клетках со знаком «–» и на эту величину увеличивается поставки в клетках со знаком «+». Для таблицы 6.4 наибольшая по абсолютной величине оценка равна 6. Строим прямоугольный контур (таблица 6.4). Наименьшая величина в клетках со знаком «–» равна 30. Получаем:

Таблица 6.5