Примеры позиционных и метрических задач на плоскость

 

Пример 1. В плоскости, заданной треугольником АВС, построить точку D (рис. 3.21).

Решение.

1. Необходимо в данной плоскости провести прямую. Зададим для этого две точки, заведомо лежащие в данной плоскости. Одной из таких точек может быть вершина А(А₁;А₂) треугольника. Вторую точку Е(Е₁;Е₂) зададим на стороне ВС. Через одноименные проекции А₁ и Е₁, А₂ и Е₂ проведем прямые. Эти прямые являются проекциями прямой. Лежащей в данной         плоскости.

2. На построенной прямой АЕ зададим точку D. Для этого построим D₁А₁Е₁ и D₂А₂Е₂. Точка D лежит в заданной плоскости, т.к.к она принадлежит прямой АЕ, лежащей в этой плоскости

 

Рис. 3.21

 

            Пример 2. Построить линию наибольшего уклона плоскости, заданной параллельными прямыми а(а₁; а₂) и b(b₁; b₂) и определить угол  между этой плоскостью и горизонтальной плоскостью проекций (рис. 3.22)

 

Рис. 3.22

 

            Решение

1. Проведем горизонталь h данной плоскости (см. гл.3 рис. 3.3, в). Проекциями этой горизонтали будут прямые h₁ и h₂.

2. Проведем прямую, перпендикулярную к горизонтальной проекции горизонтали, и отметим точки С₁ - пересечения её с h₁ D₁ – са₁. Прямая С₁D₁ является горизонтальной проекцией линии наибольшего ската.

3. Построим фронтальные проекции С₂ и D₂. Для этого из С₁ и D₁ проведем вертикальные линии связи до пересечения соответственно с h₂ и а₂.

4. Прямая, соединяющая точки С₂ и D₂, является фронтальной проекцией линии наибольшего уклона.

5. Угол  определяем из прямоугольного треугольника D₁C₁E₀, построенного на С ₁D₁ как на катете. Второй катет D₀D₁ = E₂D₂. Искомый угол =D₀C₁D₁

 

Пример 3. Задана плоскость пересекающимися прямыми АВ и CD. Определить лежит ли прямая KL в этой плоскости.

 

Рис. 3.23

 

Решение.

1.      Обозначим точки пересечения фронтальных проекций прямых АВ и KL через 1₂ и прямых CD и KL через 2₂.

2.      Строим их горизонтальные проекции – точки 1₁ и 2₂ на горизонтальной проекции (K₁L₁) прямой KL. Из построения видно, что точки 1(1₁1₂) и 2(2₁2₂) прямая KL на заданной плоскости не лежат. Следовательно, прямая KL в плоскости не лежит. Решение этой задачи можно начать и с пересечения горизонтальных проекций.

 

Пример 4. В плоскости, заданной двумя параллельными прямыми АВ и CD, провести фронталь на расстоянии 15 мм от фронтальной плоскости проекций (рис. 3.24)

Рис. 3.24

 

Решение. Проводим на расстоянии 15 мм от оси проекций параллельную  ей горизонтальную проекцию (1₁-2₂) фронтали, которая пересекает прямые А₁В₁ и C₁D₁ в точках 1₁ и 2₂.

Затем находим точки 1₁ и 2₂ на прямых А₂В₂ и C₂D₂ и проводим через них фронтальную проекцию (1₂2₂) фронтали.

 

Пример 5. Найти прямую пересечения плоскостей Р и Q.

 

Рис. 3.25

 

Решение. Плоскость Р и Q пересекаются по прямой общего положения, проходящей через точку-след (М₁;М₂) пересечения горизонтальных следов плоскостей. Точка-след (N₁;N₂) пересечения фронтальных следов плоскостей недоступна, т.к. эти следы плоскостей по заданию, в пределах чертежа не пересекаются.

Вместо точки (N₁;N₂) необходимо найти другую произвольную точку прямой пересечения, общую для заданных плоскостей. Для этого вводим вспомогательную плоскость R, например параллельную П которая, как известно, пересекает каждую из данных плоскостей по горизонтали. На их пересечении получаем вспомогательную точку (К₁;К₂), общую для данных плоскостей. Найдя эту вторую точку (К₁;К₂) прямой, проводим её проекцию: горизонтальную – через точки М₁ и К₁ и фронтальную через точки М₂ и К₂.

 

 

 

 

Пример 6. Найти точку пересечения прямой АВ с плоскостью Р (рис. 3.26)

 

Рис. 3.26

 

Решение. Обозначим искомую точку через точку К. Так как точка К (К₁;К₂) лежит на профильно-проецирующей плоскости. То её профильная проекция (К₃) должна лежать на профильном следе (Р₃) плоскости. Вместе с тем, так как эта же точка лежит и на прямой АВ, то её профильная проекция (К₃) должна лежать так же где-то на профильной проекции (А₃В₃) прямой. Следовательно искомая точка должна лежать на их пересечении. Найдя профильный след плоскости и профильную проекцию прямой, получаем на их пересечении профильную проекцию (К₃) искомой точки. Зная профильную проекцию (К₃) искомой точки, находим две другие её проекции на одноименных проекциях прямой.

 

Пример 7. Даны плоскость Р и точка А. Определить расстояние то точки до плоскости (рис. 3.27)

 

 

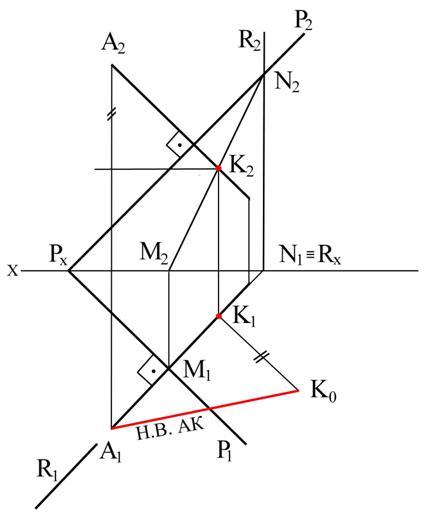
Рис. 3.27

 

Решение. Опускаем из точки А (А₁;А₂) перпендикуляр на плоскость Р и находим его основание на этой плоскости, для чего ищем точку К (К₁;К₂) пересечения перпендикуляра с плоскостью. Имея проекции (А₁К₁;А₂К₂) отрезка перпендикуляра, определим его действительную величину методом прямоугольного треугольника.

 

Пример 8. Даны треугольник АВС и точка К. Определить расстояние между ними. (рис. 3.28)

 

Рис. 3.28

 

Решение. Опускаем из заданной точки Е (Е₁;Е₂) перпендикуляр на плоскость треугольника: К₁Е₁ перпендикулярно горизонтальной проекции горизонтали (К₁Е₁С₁F₁), К₂Е₂ перпендикулярно фронтальной проекции фронтали (К₂Е₂А₂ D₂). Находим точку пересечения перпендикуляра с плоскостью треугольника (К₁;К₂) , определяем натуральную величину отрезка перпендикуляра (К₁Е₁;К₂Е₂) методом прямоугольного треугольника.