Упражнение 5

Доказать, что если R  W  W – рефлексивно, то А  А – тавтология относительно шкалы (W, R) для любой формулы А.

Формула (А  В)  (А  В) является тавтологией относительно класса всех шкал Крипке. Такие формулы называют естественно истинными. Формула А  А верна относительно некоторого класса шкал. Такие формулы называются условно истинными.

6.3. Алгоритмическая логика Хоара

Интуитивно программа понимается как набор операторов, переводящих машину из одних состояний в другие. Хоар предложил для отладки и верификации программ рассматривать формулы, описывающие состояния машины перед выполнением (предусловие) и после выполнения (постусловие) программы. Программе  сопоставлялась запись: {А}{В}, означающая, что предусловие описывается формулой А, а постусловие формулой В. Пратт предложил запись: А  []В – если перед выполнением программы состояние машины описывается формулой А, то после выполнения верна формула В. Это позволило описывать вычислительные процессы, состоящие из комплексов программ, с помощью модальной логики, рассматривая каждую программу как модальность.

Пропозициональная динамическая логика

Пусть ₀ – произвольное множество. Его элементы называются базисными программами. Предположим, что   ₀ – такое множество слов, что вместе с любыми ₁, ₂   оно содержит:

1. ₁  ₂ (неопределённый выбор одной из программ ₁ или ₂);

2. ₁ ; ₂ (выполнение ₁ ,затем ₂);

3. ₁* (выполнение ₁ конечное, возможно нулевое, количество раз);

4. ₁  ₂ (одновременное выполнение программ ₁ или ₂).

Элементы из  будем называть программами. Рассмотрим атомы из Р как простые высказывания о состояниях машины, в которую загружаются программы. Для каждой программы    обозначим через [] соответствующую ей модальность. Определим формулы пропозициональной динамической логики PDL по индукции:

1. атомы р  Р – формулы;

2. А & В, А, []А – формулы для любых формул А и В, и элемента   ;

3. все формулы PDL составляются с помощью правил 1 – 2.

Введём обозначение: <>А как сокращение для []А.

Для каждой формулы А определим программу: А?  , тестирующую, верна ли формула А. Эта программа заканчивает работу, если формула А верна, и зависает (аварийно завершает работу), если нет. Эта программа вводится с целью интерпретации оператора

if (A) then ₁ else ₂

как программы

(А?; ₁)  ((А)? ; ₂)  .

Семантика пропозициональной динамической логики

Пусть ₀ – множество базисных программ,  – множество всех программ, Р – атомные формулы, F(P) – все формулы, W – множество состояний машины, в которой могут работать программы . Для каждого    определена модальность []. Стало быть, мы должны каждому  поставить в соответствие некоторое отношение доступности R_  W  W.

Шкала Крипке (или система переходов) будет состоять из пары: (W, (R_)_), где W – множество состояний, а R_{ –} отношения R_  W  W.

Программу можно интерпретировать как множество пар (x, y)  R_ таких, что после выполнения программы  машина из состояния х перейдёт в состояние y. Каждому атому p  P ставится в соответствие подмножество h(p)  W состояний, при которых высказывание р верно.

Интерпретацией называется тройка M = (W, (R_)_, h), состоящая из шкалы Крипке и оценки h : P  P(W), удовлетворяющих соотношениям:

1. R_  _ = R_  R_;

2. R_ ; _ = R_  R_;

3. ;

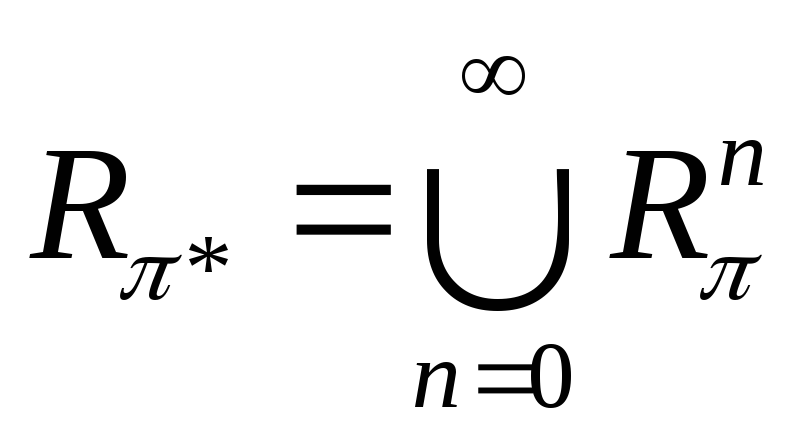4. R_A? = {(x, x) : x  W и M, x |= A}.

Здесь R_* – наименьшее рефлексивное транзитивное отношение, содержащее R_. Расширим h на множество формул F(P), полагая t  h(A), если и только если M, t |= A. Получим соотношения:

5. h(A  B) = h(A)  h(B);

6. h(A) = W \ h(A);

7. h(<>A) = {t  W : (t, u)  R_ для некоторого u  h(A)}.

В некоторых случаях под семантикой логики PDL понимают шкалу с расширенной на F(P) оценкой, удовлетворяющие соотношениям 1 – 7.