Тема 10: функции нескольких переменных
-
Частная производная
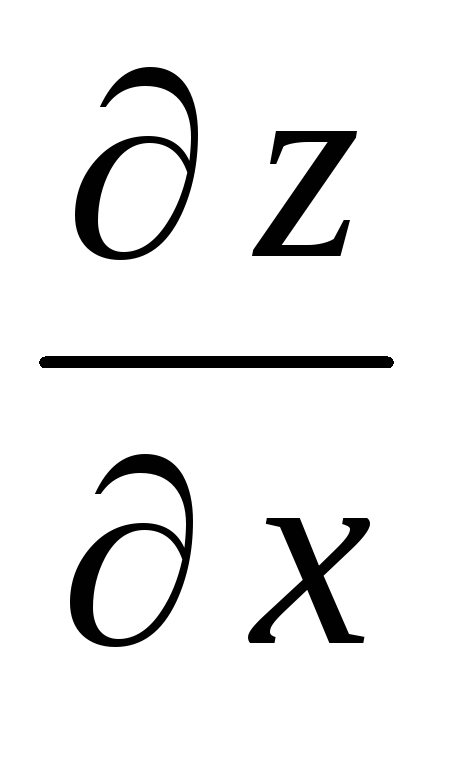от функции
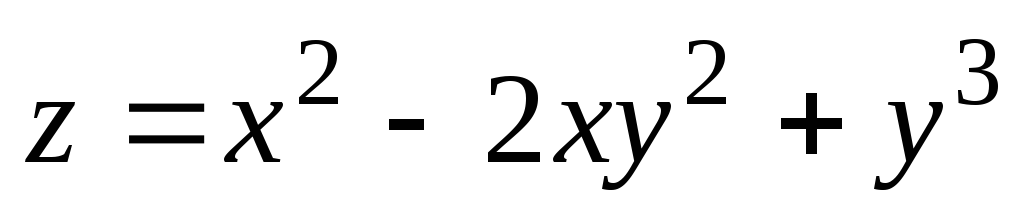равна
а) 2 (х – у2);
б) y (3 y – 4 x);
в) 2 x – 4 y;
г) – 2 x + 3 y.
-
Частная производная
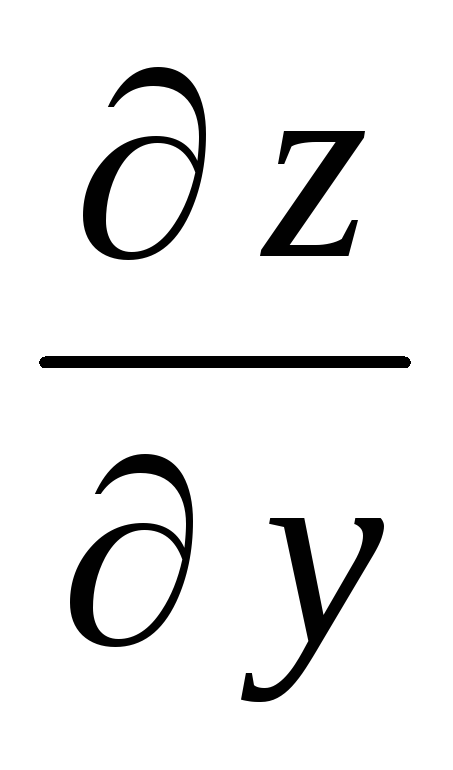от функции
равна
а) cos (x + y);
б) – cos (x + y);
в) sin x;
г) cos y.
-
Частная производная
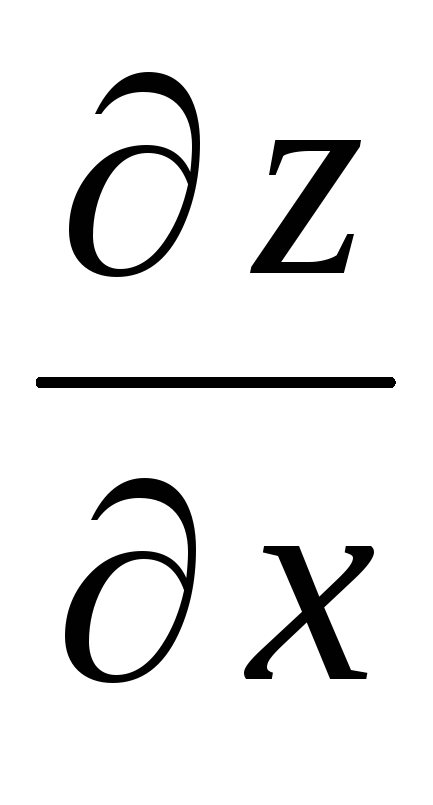от функции
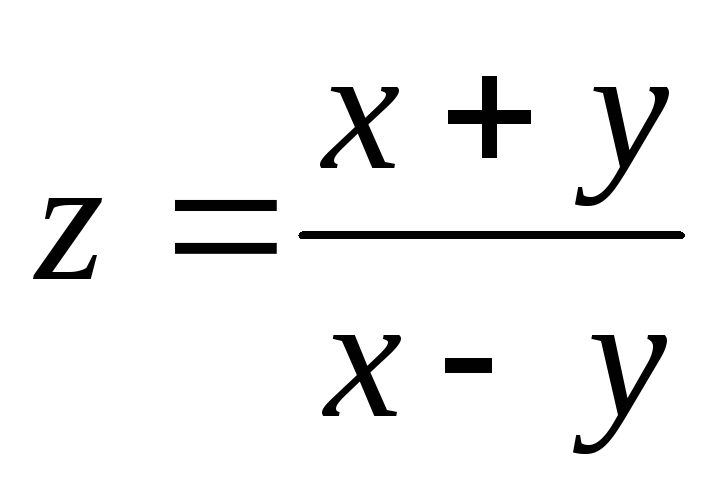равна
а)
;
б)
;
в)
;
г)
.
-
Найдите значения частных производных функции
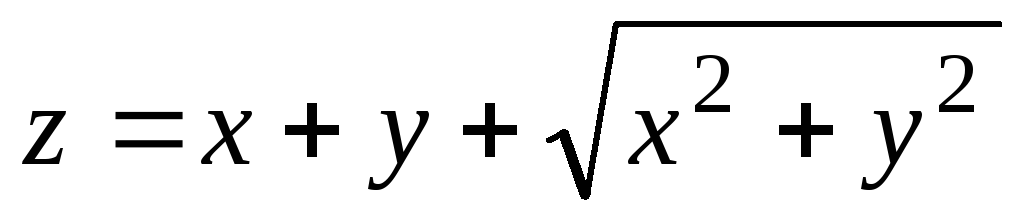в
точке М
(3; 4).
а)
,
;
б)
,
;
в)
,
;
г)
,
.
-
Найдите производную
,
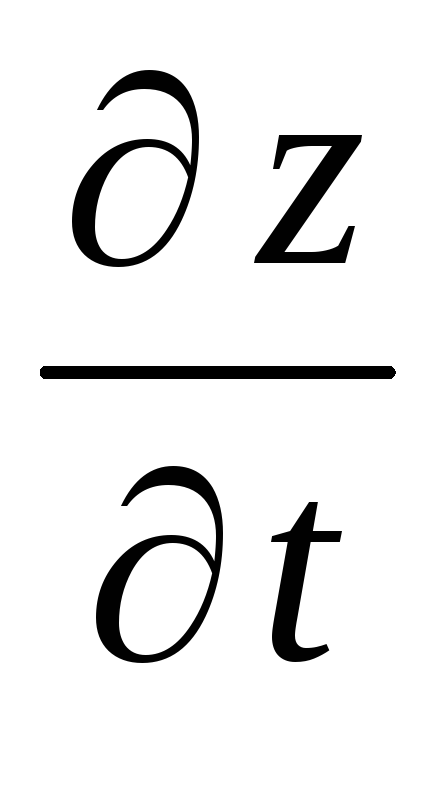если
,
,
.
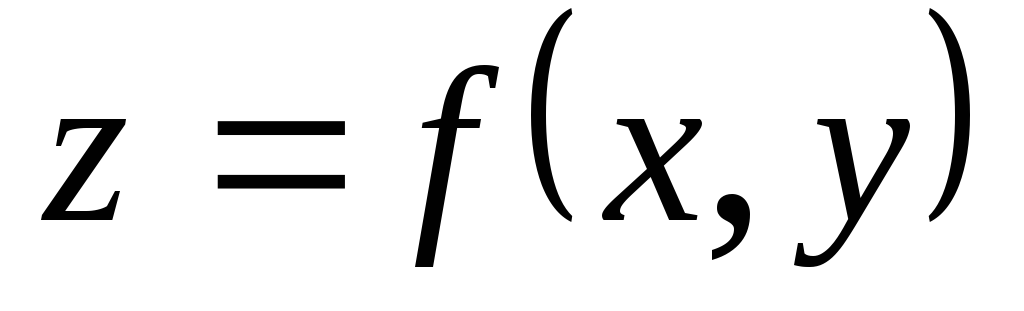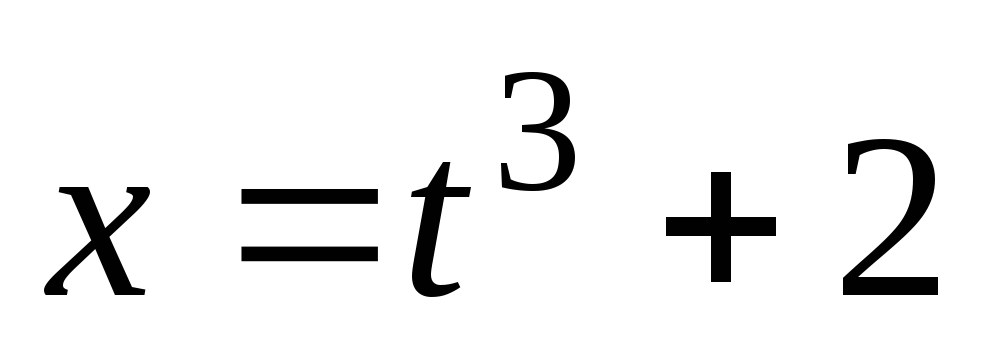а)
;
б)
;
в)
;
г)
.
-
Найдите производную
,
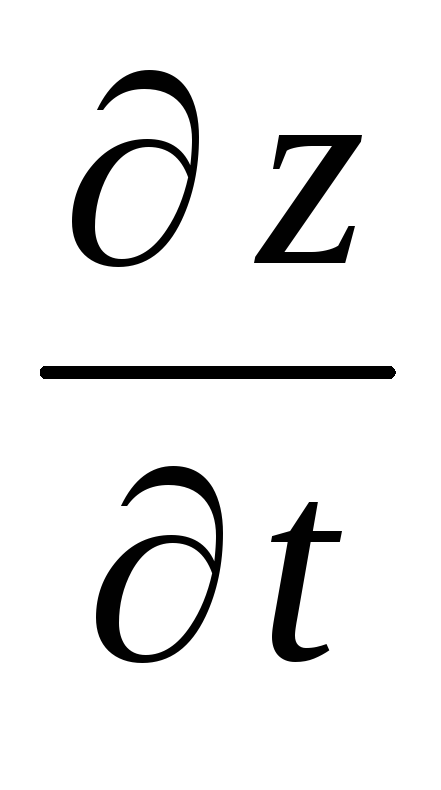если
,
,
.
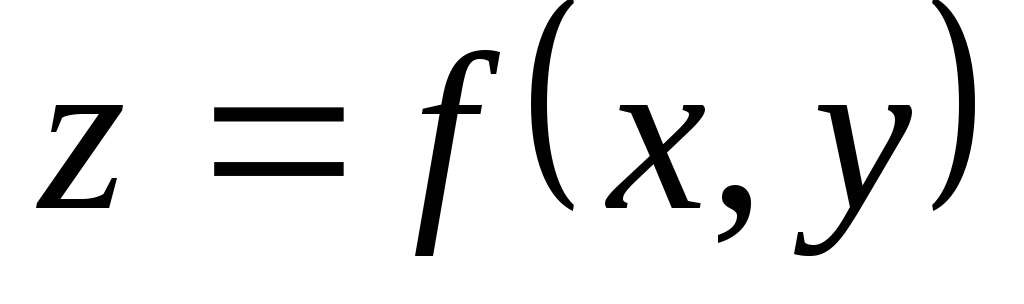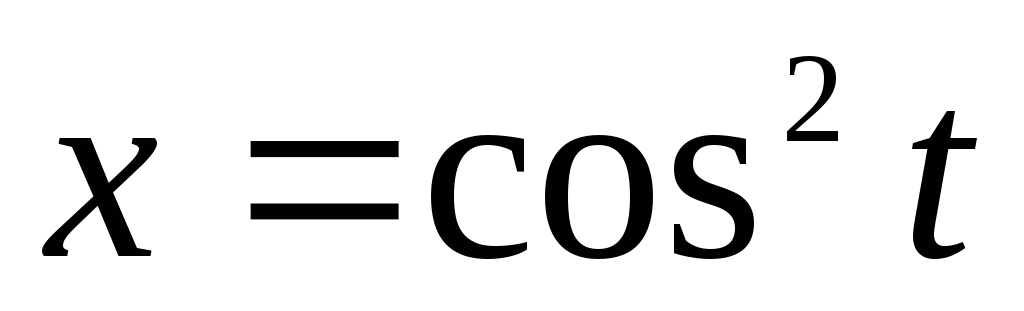а)
;
б)
;
в)
;
г)
.
-
Частная производная второго порядка
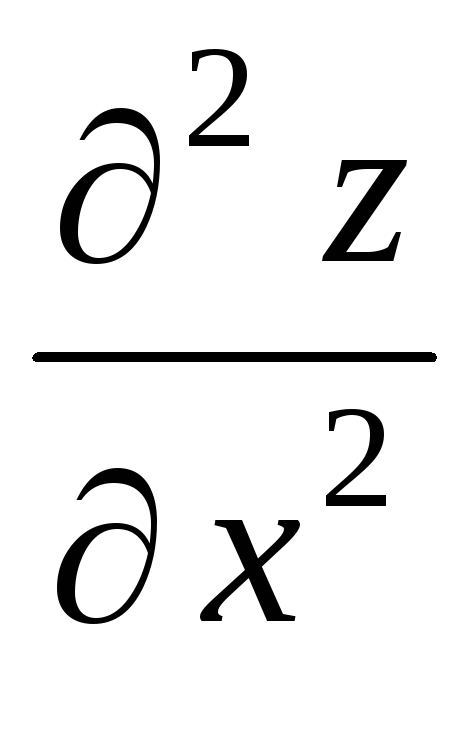от функции
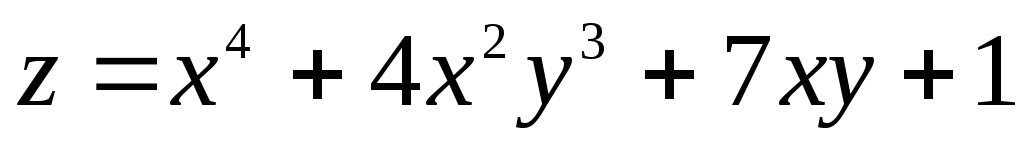равна
а) 12 х2 + 8 у3;
б) 24 х2 у;
в) 24 х у2 + 7;
г) – 7 – 24 х у2.
-
Частная производная второго порядка
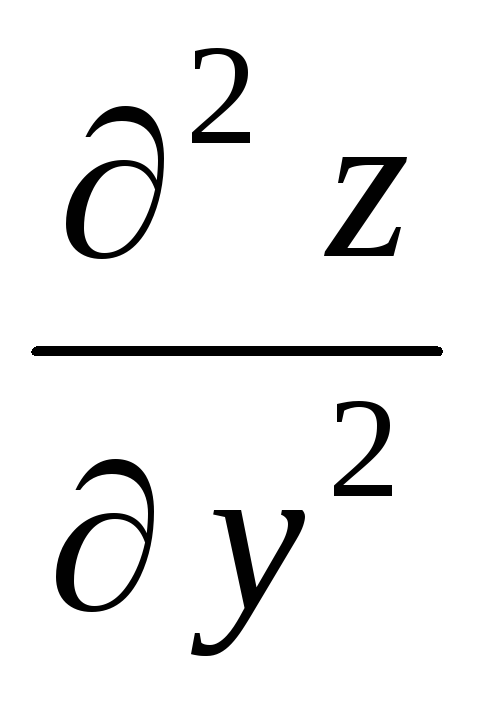от функции
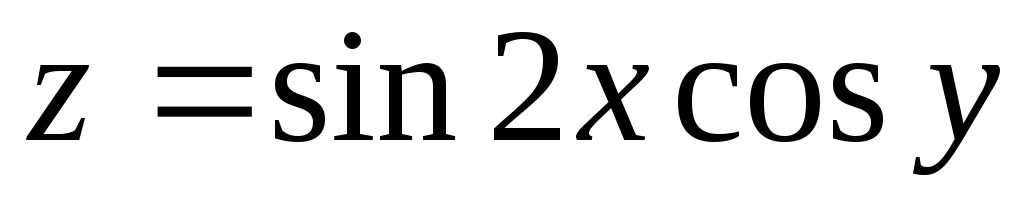равна
а)
;
б)
;
в)
;
г)
.
-
Частная производная второго порядка
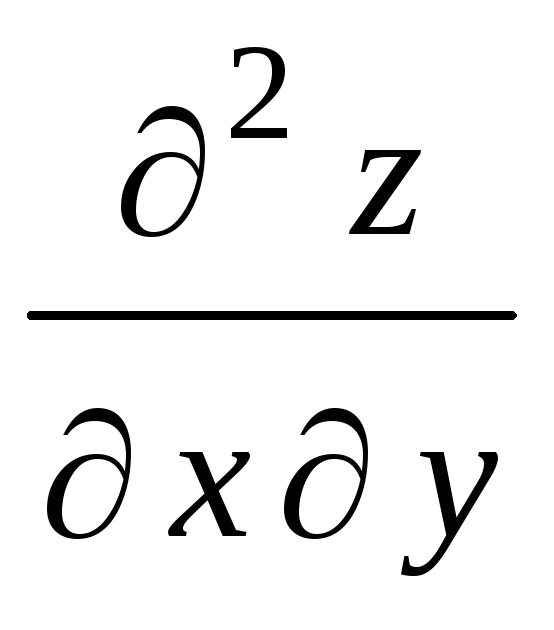от функции
равна
а) 0;
б) х;
в)
;
г)
.
-
Найдите повторный интеграл
.
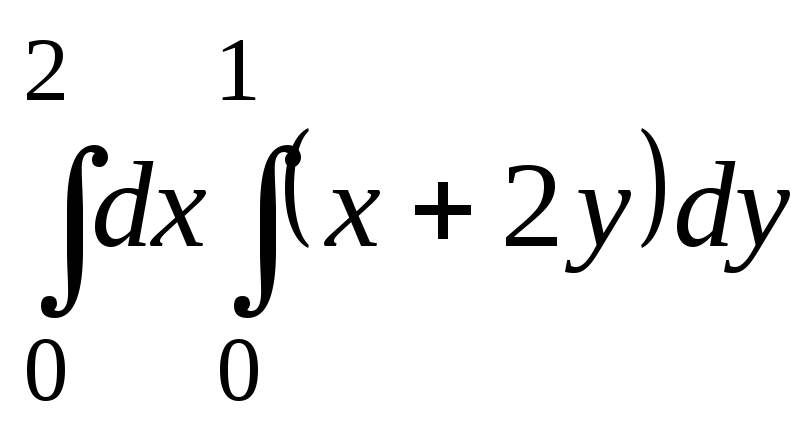а)
;
б)
;
в)
;
г) 4.
-
Найдите повторный интеграл
.
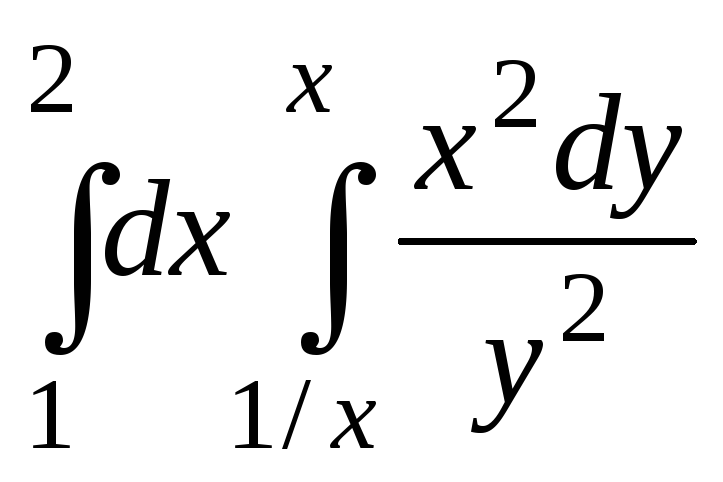а)
;
б) 2;
в)
;
г) 1.
-
Найдите двойной интеграл
,
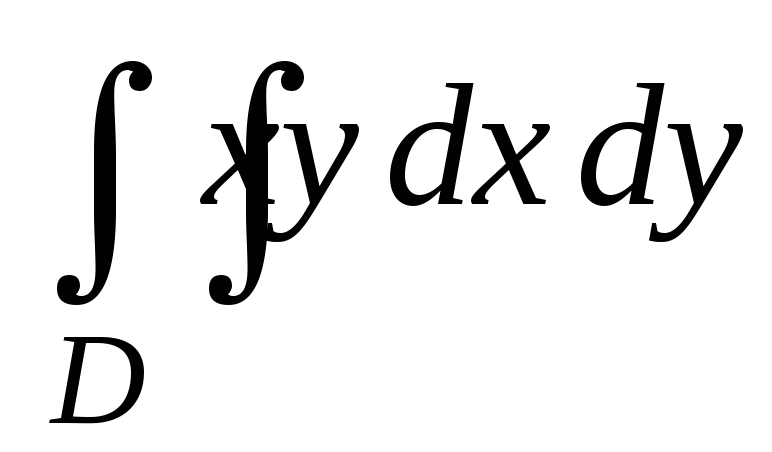если 3
х
5, 0
у
1.
а) 4;
б) 8;
в)
;
г) – 4.
-
Найдите двойной интеграл
,
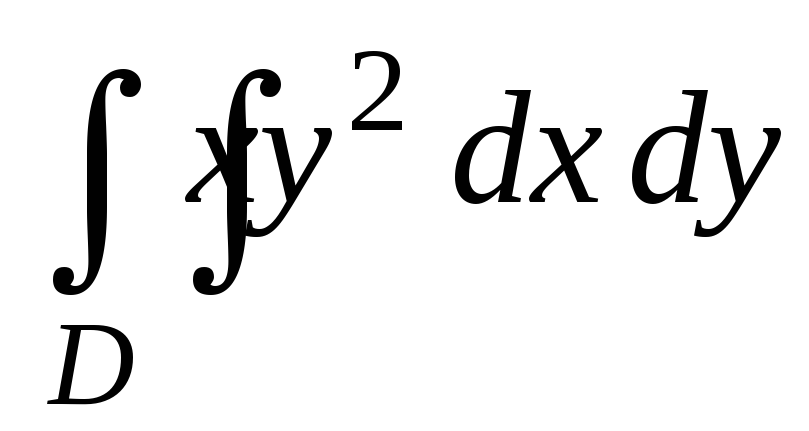если 2
х
4, 0
у
1.
а) 2;
б)
;
в)
;
г) 1.
-
Найдите двойной интеграл
,
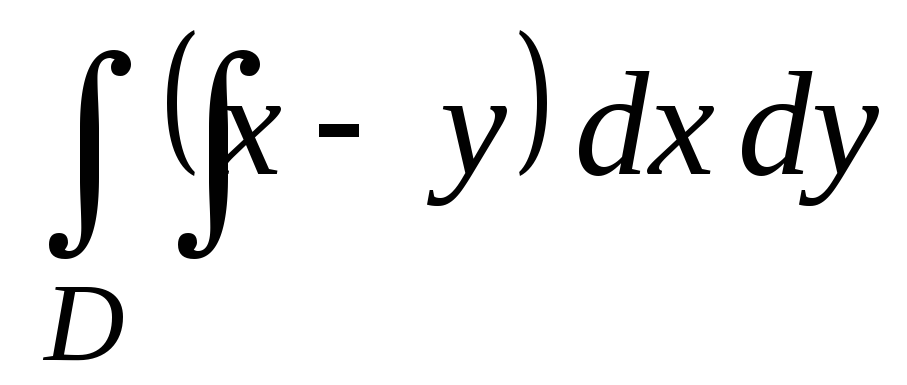если 1
х
4, 1
у
3.
а) 3;
б)
;
в) 4;
г) – 4.
-
Найдите двойной интеграл
,
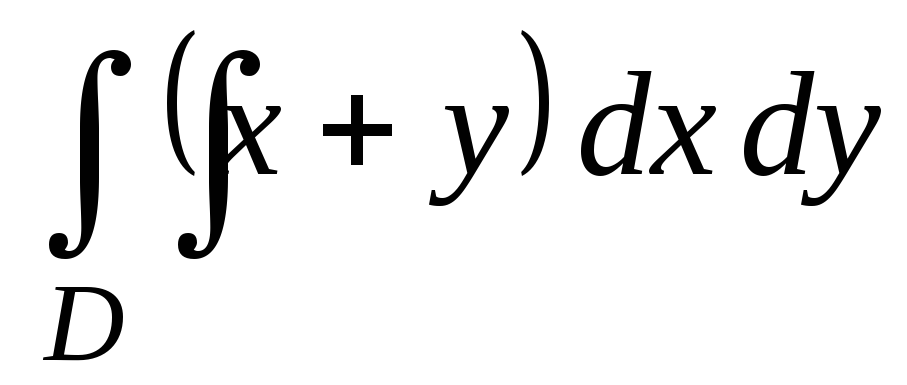если 3
х
5, 0
у
2.
а) 20;
б)
;
в) 8;
г)
.
-
Найдите двойной интеграл
,
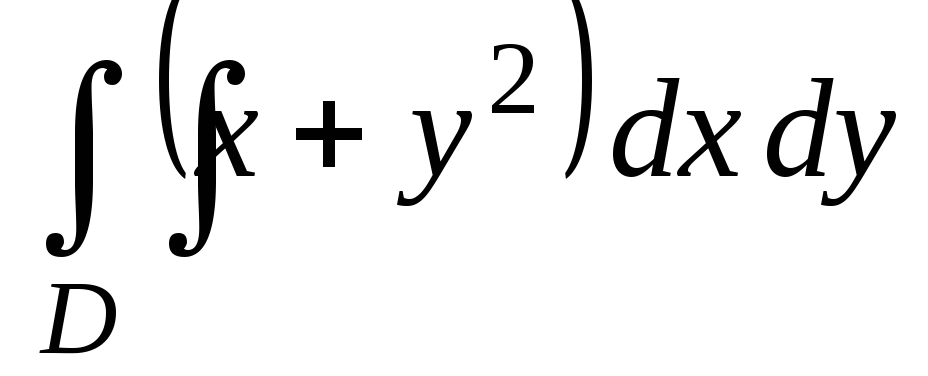если 2
х
3, 1
у
2.
а) 20;
б)
;
в) 4;
г)
.
-
Найдите двойной интеграл
,
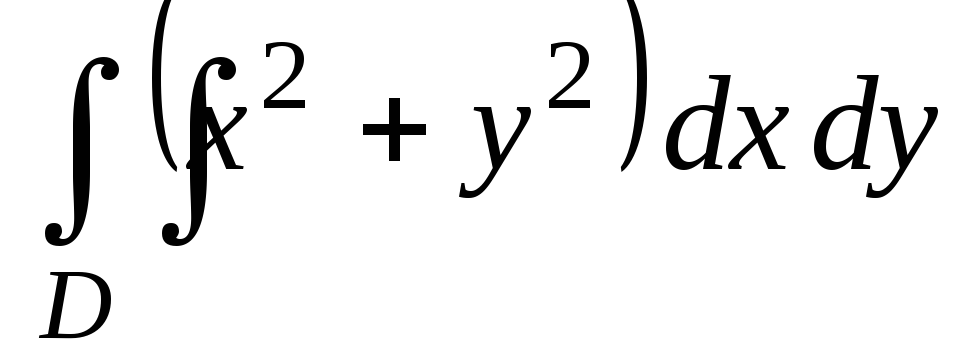если 0
х
1, 0
у
1.
а) 1;
б)
;
в) – 1;
г)
.
-
Найдите двойной интеграл
,
если 0
х
1, – 1
у
0.
а) 1;
б) 0;
в) е;
г)
.
-
Найдите тройной интеграл
по области V,
ограниченной поверхностями: х
= 0, х
= 1, y
= 0, y
= 1, z
= 0, z
= 1.
а) 1;
б) 2;
в)
;
г)
.
-
Найдите тройной интеграл
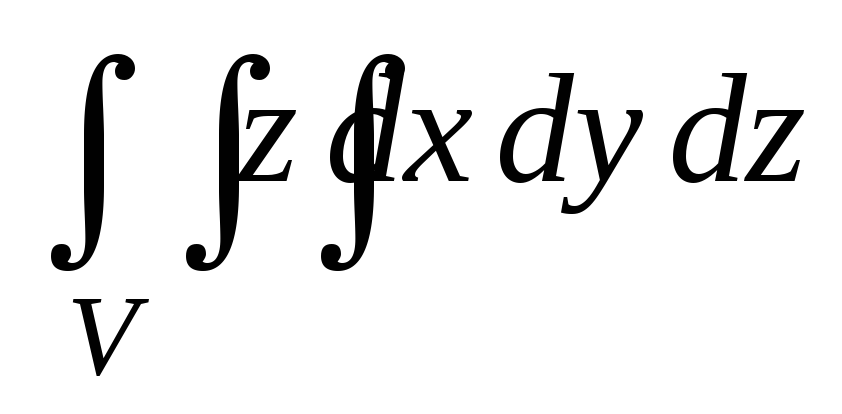по области V,
ограниченной поверхностями: х
= 0, y
= 0, z
= 0, х
+ y
+ z
= 1.
а) 1;
б) 24;
в)
;
г)
.
Тема 11: дифференциальные уравнения
-
Укажите, какое из следующих уравнений является дифференциальным. а) y = x е у; б) y = 2x2 – 5x + 7; в) y = x2 + С х; г) ln
= 1 + C
y. -
Укажите, какое из следующих уравнений является дифференциальным. а) y – tg x y = 0; б) C y = (x2 + y2); в) y = sin C x; г) y = x3 + x2 + 5.
-
Укажите обыкновенные дифференциальные уравнения. а) y = х2 – у2; б)
;
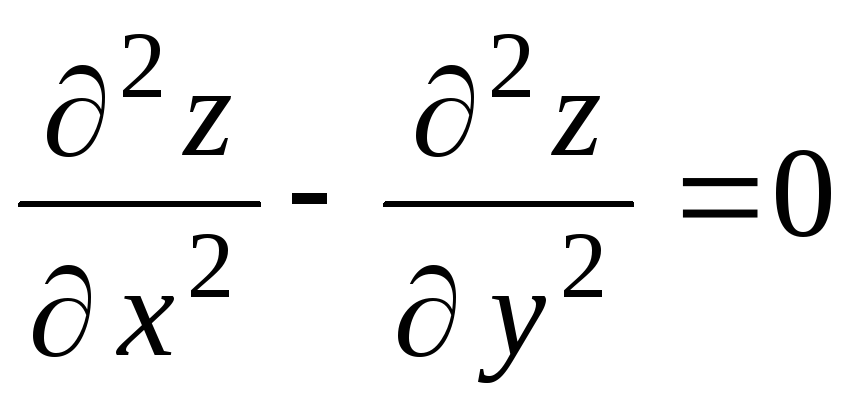в)
у2
= х2
+ ln
у;
г)
. -
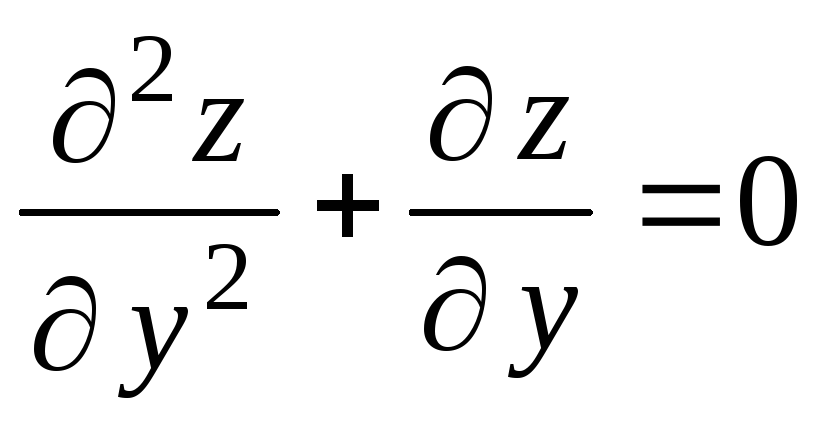Укажите обыкновенные дифференциальные уравнения. а) y = х3 + ln у; б)
;
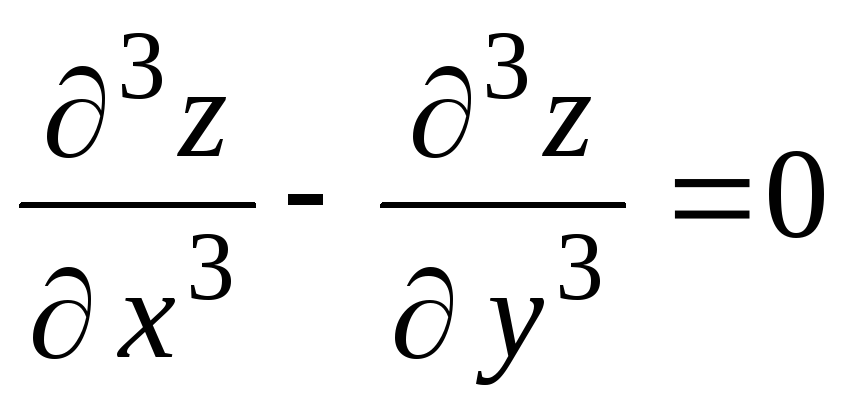в)
у2
= х2
+ е х;
г)
. -
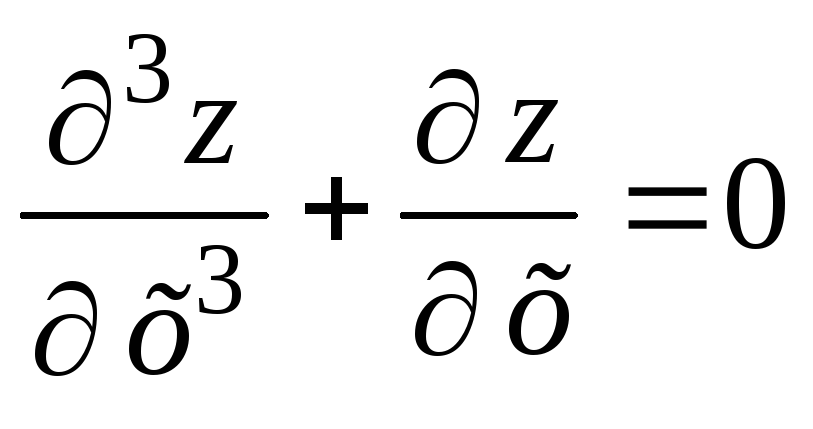Укажите дифференциальное уравнение в частных производных. а)
;
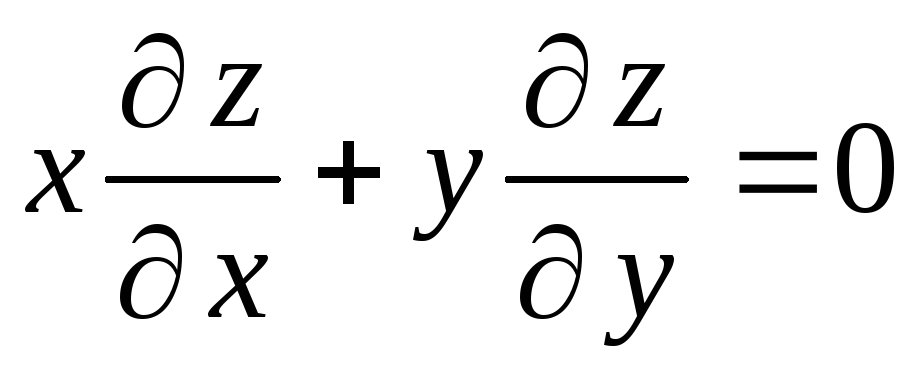б)
;
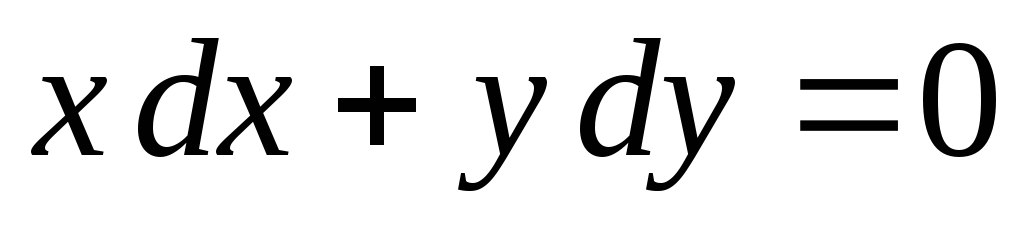в)
y
= х2у;
г)
х y
– у
= х4
у2. -
Укажите дифференциальное уравнение в частных производных. а)
;
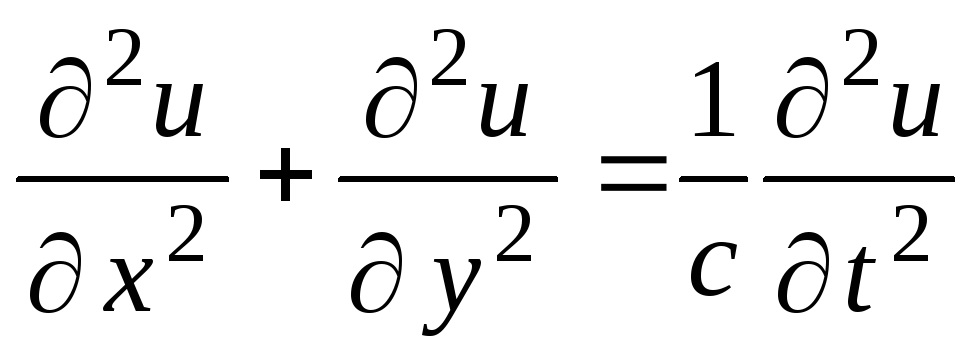б)
y
х
+ у
= – х
у2;
в)
y
= х2
+ у2;
г)
х
y
+ у
= у2
ln
х. -
Укажите уравнение в полных дифференциалах. а) (х + у + 1) dx + (x – y2 + 3) dy = 0; б) х у dx + х2 у2 dy = 0; в) х2 dy – у2 dx = 0; г) (х + у + 1) dx – (x – y2 + 3) dy = 0.
-
Укажите уравнение в полных дифференциалах. а)
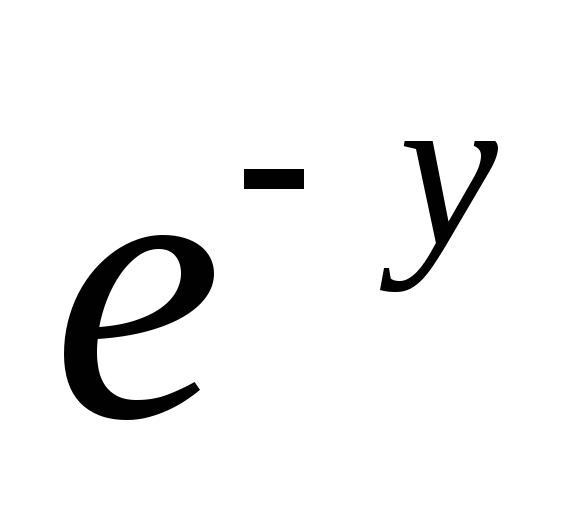dx
+ (1 – x
)
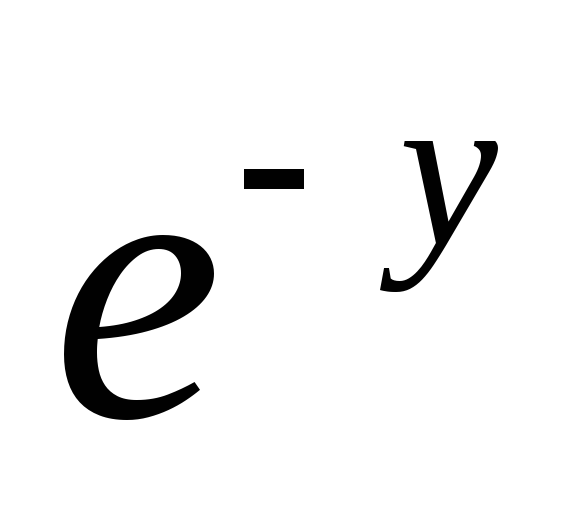dy
= 0;
б) х
y
+ 2 у x
= 0;
в)
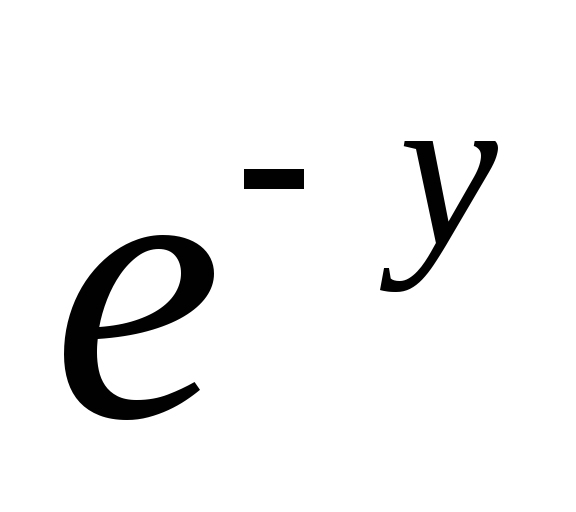dx
– (1 – x
)
dy
= 0;
г) ) х
y
– 2 у x
= 0. -
Найдите общее решение ДУ y – xy = 1 + x2y с разделяющимися переменными:
а)
y
=
+ 1;
б) y
=
+ С;
в) y
=
+ С;
г) y
=
– 1.
-
Найдите общее решение ДУ y =
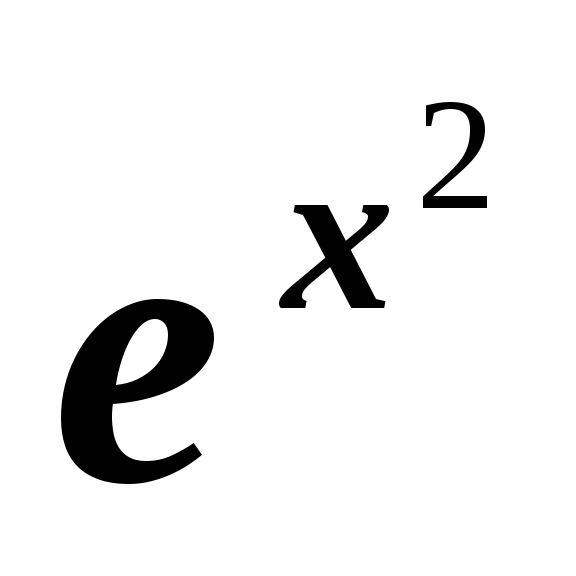x(1
+ y2)
с разделяющимися переменными:
а) y
=
+ C;
б)
arctg
y
=
+ C;
в) arctg
y
=
– C;
г) 1 + y
=
+ C.
-
Найдите общее решение ДУ yctg x + y =2 с разделяющимися переменными:
а) y = C cos x+2;
б) y = C ctg x+2;
в) y = C tg x+2;
г) y = C sin x +2.
-
Найдите общее решение ДУ y y+ х = 0 с разделяющимися переменными:
а)
б)
;
в)
;
г)
.
-
Найдите общее решение ДУ ytg x – y = 1 с разделяющимися переменными:
а)
;
б)
;
в) y = C ctg x + 1;
г) y = C tg x + 1.
-
Найдите общее решение ДУ ysin2 x = y с разделяющимися переменными:
а)
;
б)
;
в) y = – ctg x + C;
г) y = ln (ctg x) + C.
-
Найдите общее решение ДУ 2
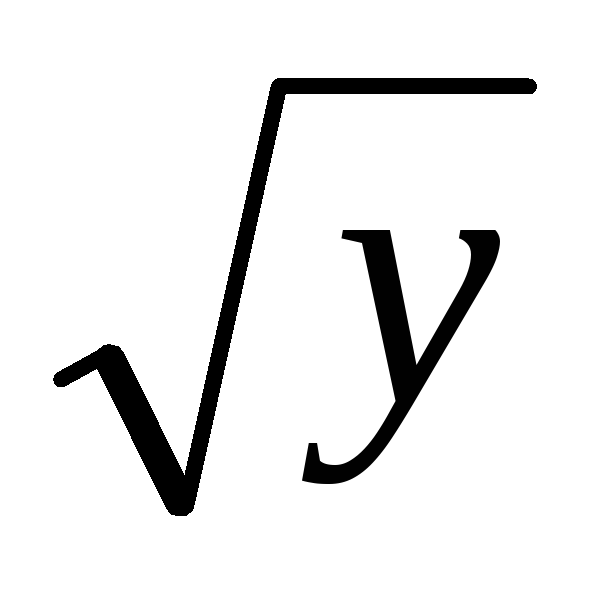dx
= dy
с разделяющимися переменными:
а)
;
б)
;
в)
;
г)
.
-
Найдите общее решение ДУ x y – y= 0 с разделяющимися переменными:
а)
;
б)
;
в)
;
г)
.
-
Найдите общее решение ЛДУ первого порядка y– y = е х:
а) y = (x + C) e x;
б) y = x + C e x;
в) y = x + 2 e x;
г) y = x e x.
-
Найдите общее решение ЛДУ первого порядка y= х + y:
а) y = C e x – x – 1;
б) y = C e x + x – 1;
в) y = C e x – x e x – 1;
г) y = e x – x – 1.
-
Найдите общее решение ЛДУ первого порядка x y+ y = 3:
а)
y
= 3 +
;
б) y = 3 + C x;
в) y
= 3 –
;
г) y
= 3 +
e
x
.
-
Найдите общее решение ЛДУ первого порядка x y+ y = e x:
а)
y
=
;
б) y
=
;
в) y
=
;
г) y
=
e
x
.