
- •Тема 1: комплексные числа
- •Тема 2: векторы. Координаты на плоскости
- •Тема 3: прямая на плоскости. Прямая и плоскость в пространстве
- •Тема 4: матрицы и определители
- •Тема 5: системы линейных уравнений
- •Тема 6: область определения функции. Предел последовательности. Предел функции
- •Тема 7: производная функции. Дифференциал. Производные и дифференциалы высших порядков
- •Тема 8: неопределенный и определенный интегралы
- •Тема 9: ряды
- •Тема 10: функции нескольких переменных
- •Тема 11: дифференциальные уравнения
- •Тема 12: основы теории вероятностей
Тема 1: комплексные числа
-
Найдите сумму чисел
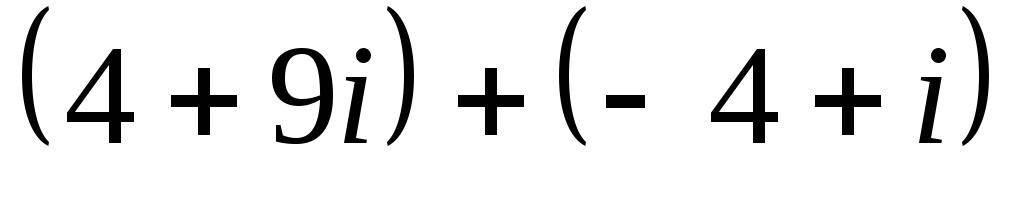 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
8.
; г)
8.
-
Найдите сумму чисел
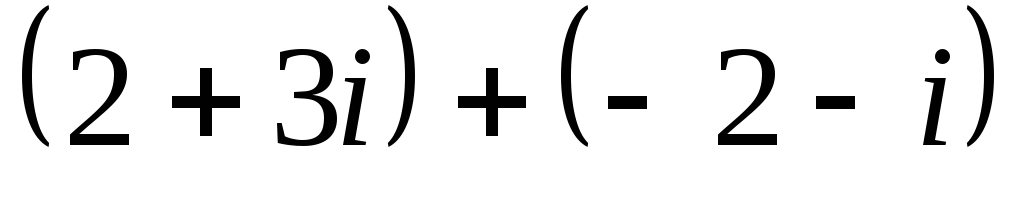 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
0.
; г)
0.
-
Найдите разность чисел
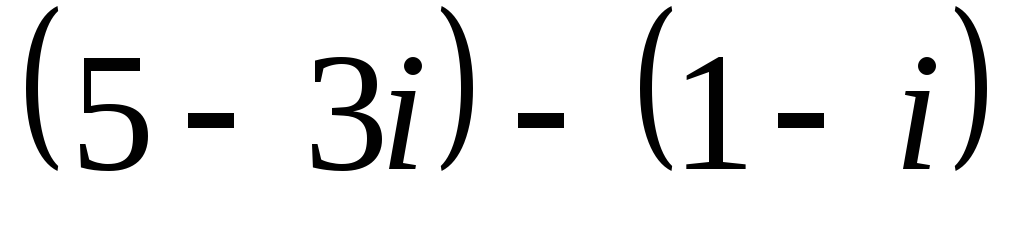 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Найдите разность чисел
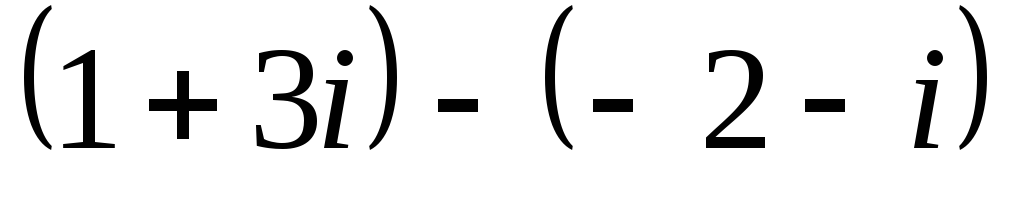 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Найдите произведение чисел
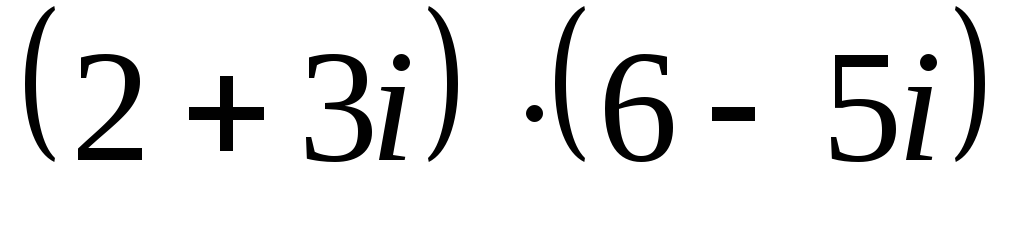 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Найдите произведение чисел
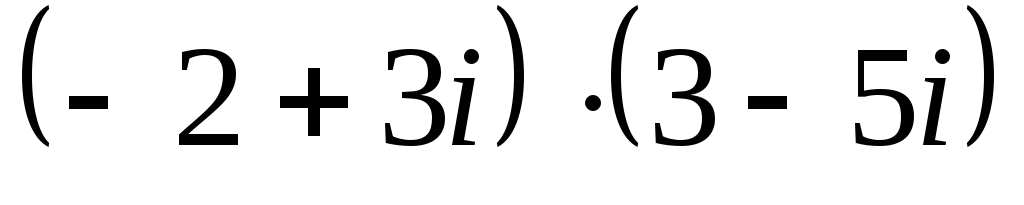 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Найдите частное чисел
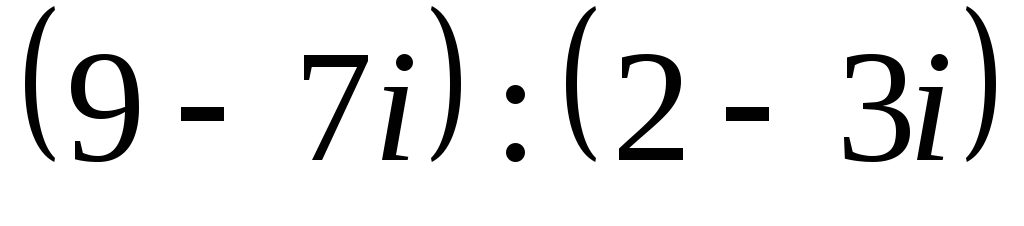 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Найдите частное чисел
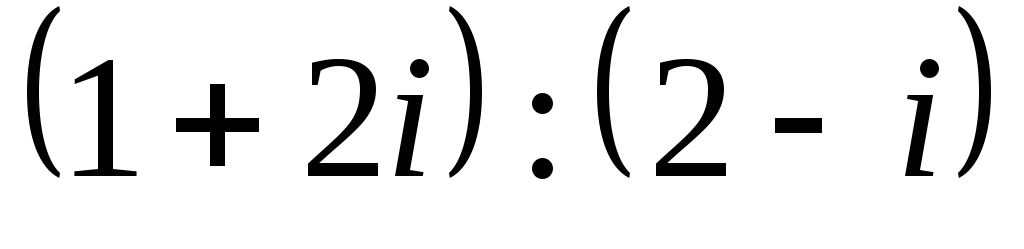 :
:
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Возведите в степень
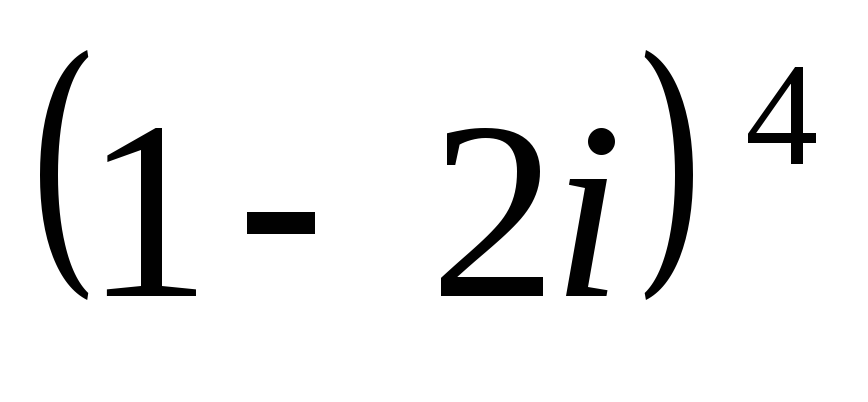 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Возведите в степень
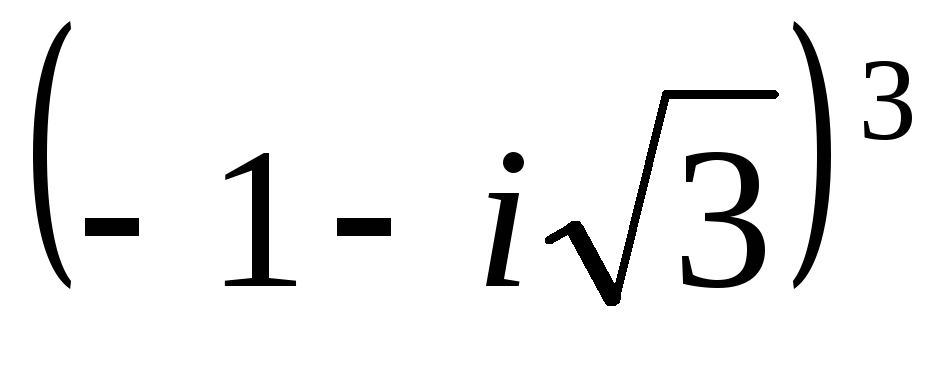 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Запишите в тригонометрической форме число
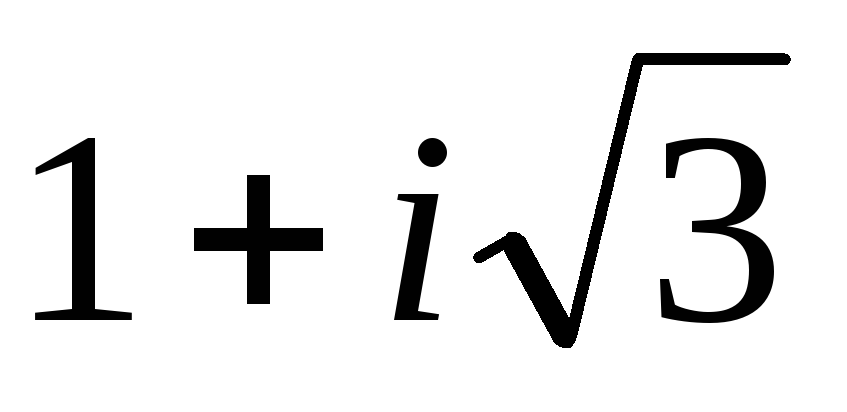 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Запишите в тригонометрической форме число
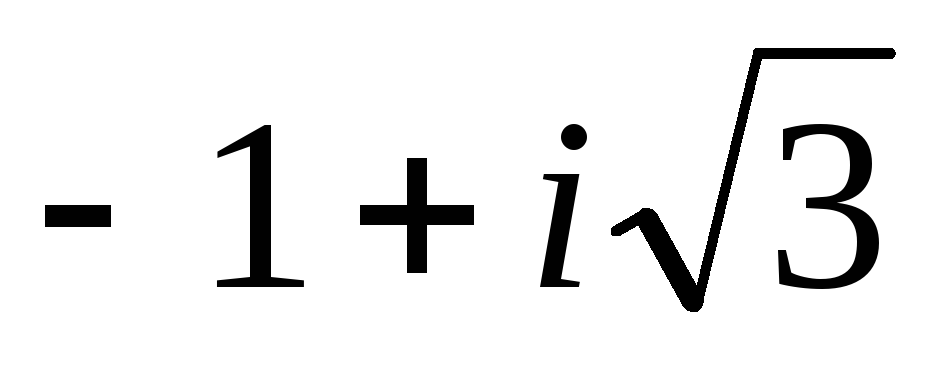 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Запишите в тригонометрической форме число
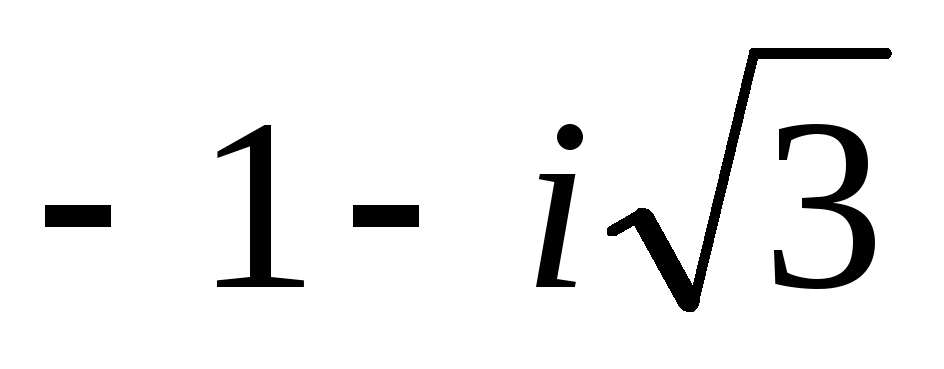 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
-
Запишите в тригонометрической форме число
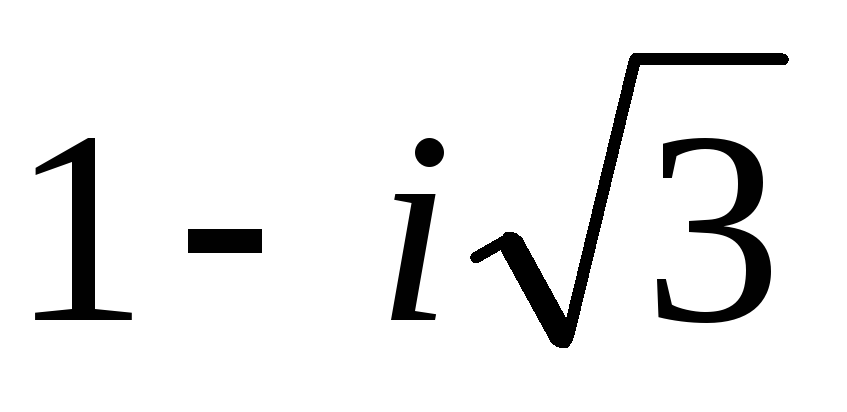 .
.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
Тема 2: векторы. Координаты на плоскости
-
Если
 = (1; 6),
= (1; 6),
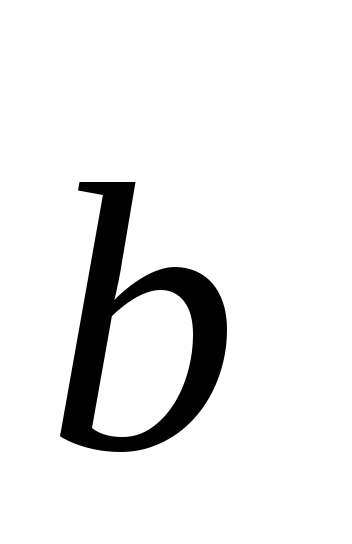 = (– 2; 3), то вектор
= (– 2; 3), то вектор
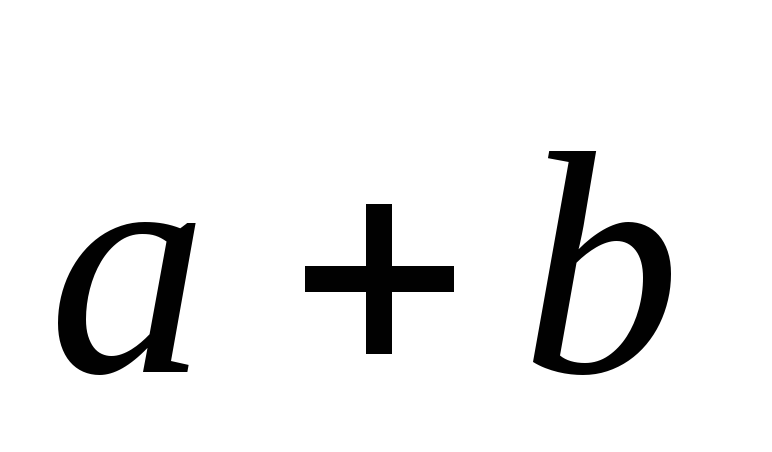 :
а)
(3; 9);
:
а)
(3; 9);
б) (3; – 3);
в) (– 1; 3);
г) (– 1; 9).
-
Если
 = (– 3; 10),
= (– 3; 10),
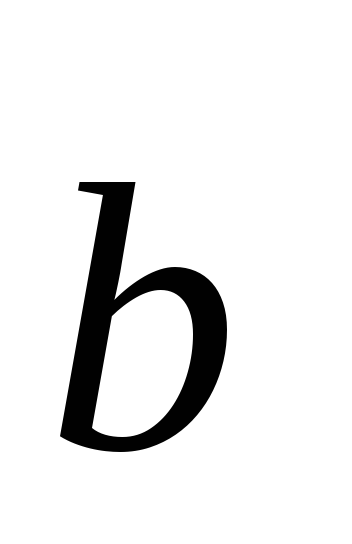 = (1; 4), то вектор
= (1; 4), то вектор
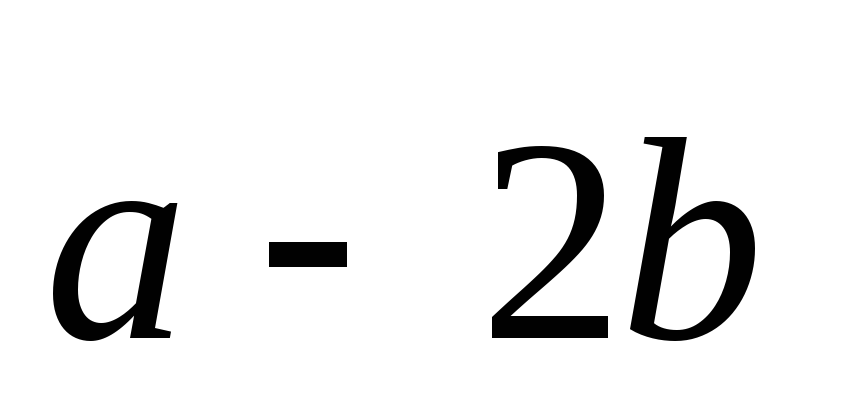 :
а)
(– 5; 2);
:
а)
(– 5; 2);
б) (– 1; 2);
в) (1; 2);
г) (– 2; 18).
-
Укажите неверное утверждение: а)
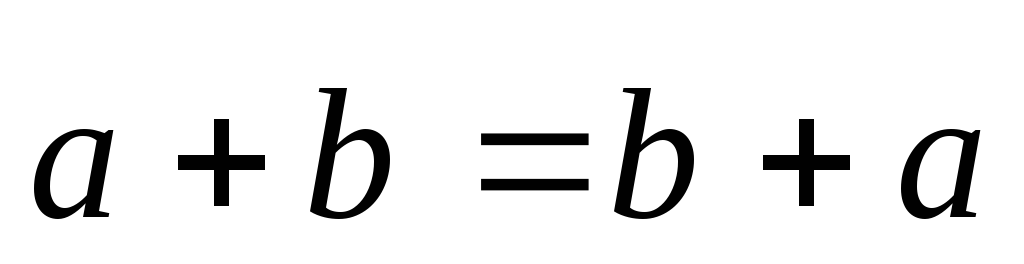 ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Укажите неверное утверждение: а)
 ;
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() .
.
-
Если A1(3; – 4; 1), A2(4; 0; – 5), то вектор
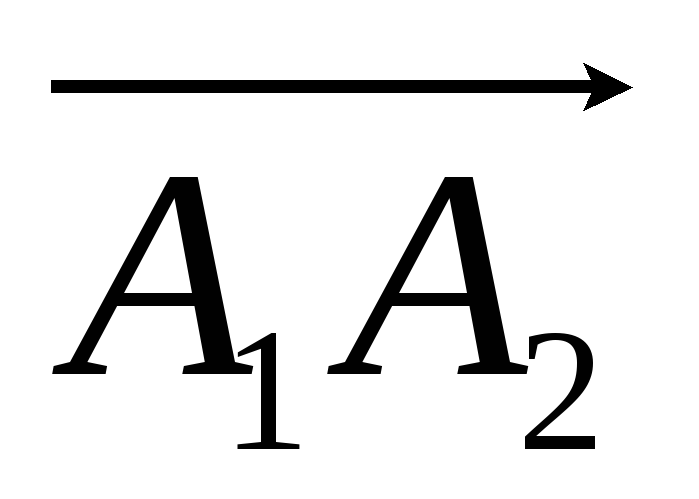 :
а)
(1; 4; – 6);
:
а)
(1; 4; – 6);
б) (7; – 4; 6);
в) (– 1; – 4; 6);
г) (8; – 4; 5).
-
Если A1(5; – 1; 2), A2(0; 3; 7), то вектор
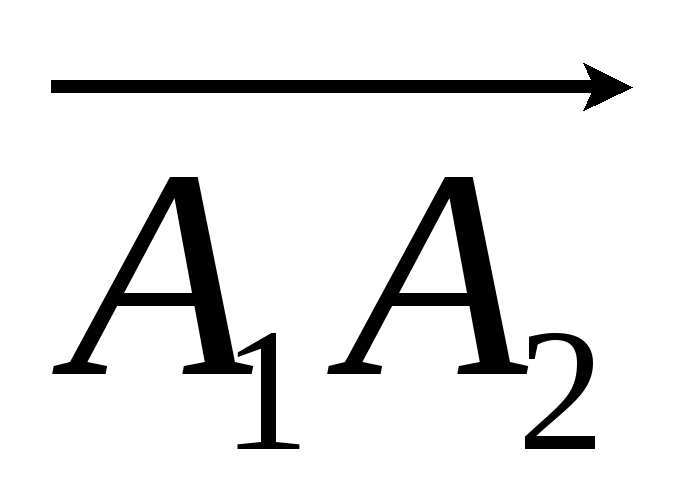 :
а)
(– 5; 4; 5);
:
а)
(– 5; 4; 5);
б) (5; – 4; – 5);
в) (5; 2; 9);
г) (0; – 3; 14).
-
Если A1(3; – 4; 1), A2(4; 0; – 5), то длина вектора
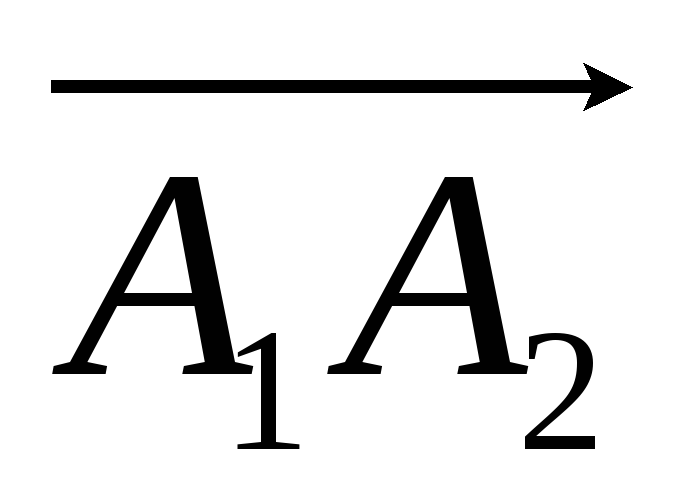 :
а)
:
а)
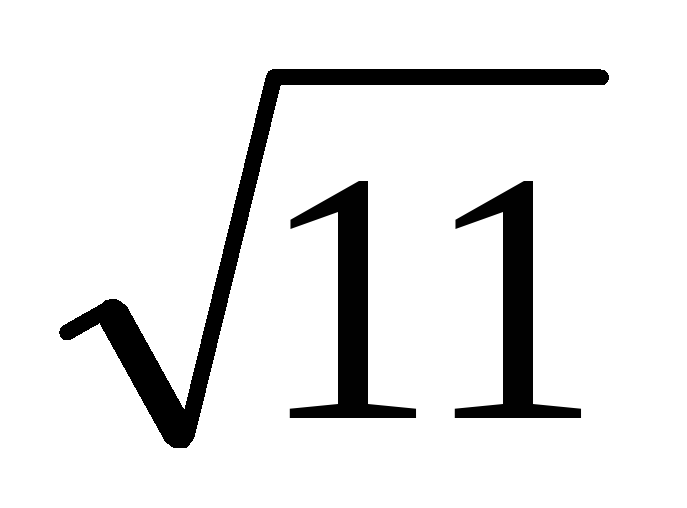 ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
-
Если A1(2; – 4; 5), A2(6; – 1; – 7), то длина вектора
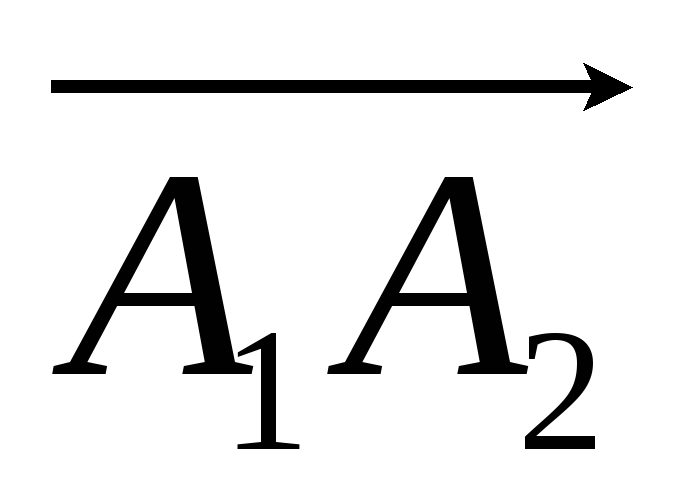 :
а)
1;
:
а)
1;
б)
![]() ;
;
в) 10;
г) 13.
-
Если A1(– 2; 2; 1), A2(4; 10; 1), то длина вектора
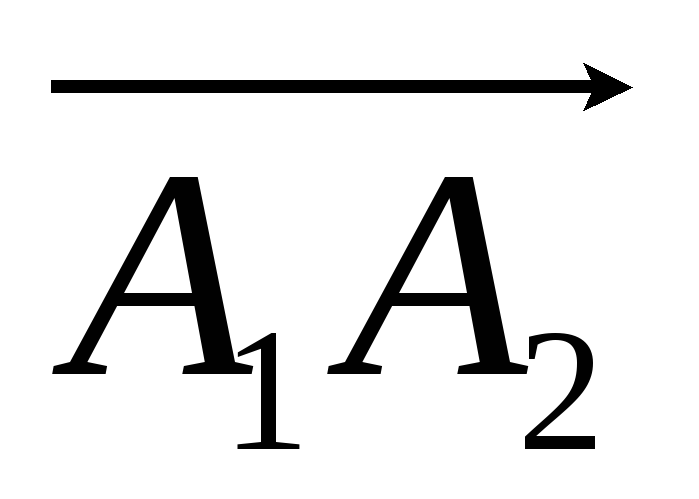 :
а)
1;
:
а)
1;
б)
![]() ;
;
в) 16;
г) 10.
-
Даны три последовательные вершины параллелограмма A(1; 1), B(2; 4), C(6; 4). Найдите координаты его четвертой вершины D. а) D (2; 5);
б) D (5; 1);
в) D (2; 1);
г) D (1; 5).
-
Даны три последовательные вершины параллелограмма A(1; 1), B(3; 4), C(7; 1). Найдите координаты его четвертой вершины D. а) D (– 3; 4);
б) D (– 5; 1);
в) D (5; – 2);
г) D (4; – 1).
-
Даны векторы
 и
и
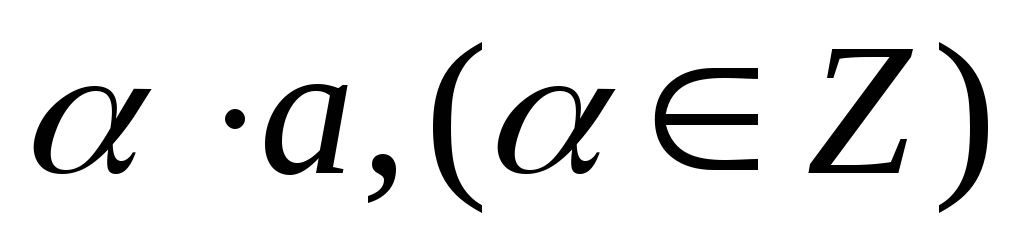 .
При каких значениях
.
При каких значениях
 эти векторы равны?
а) при
эти векторы равны?
а) при
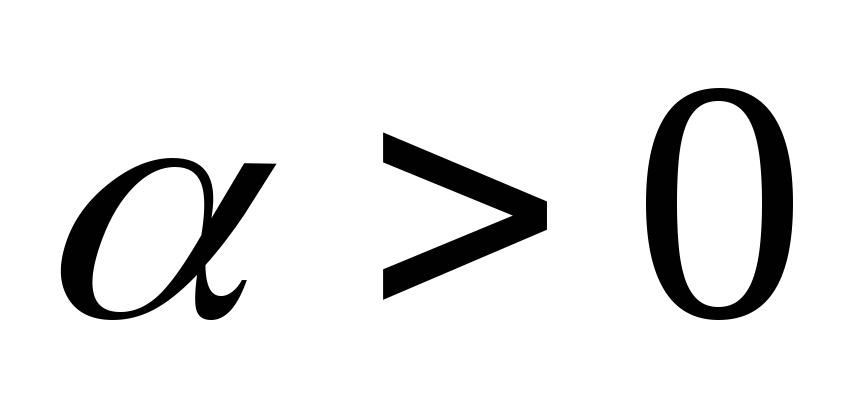 ;
;
б) при
![]() ;
;
в)
при
![]() ;
;
г) при
![]() .
.
-
Укажите вектор, коллинеарный вектору
 (2;
3; – 1).
а)
(2;
3; – 1).
а)
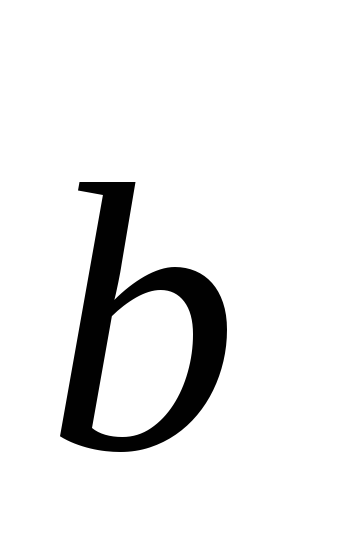 (–
4; – 6; 2);
(–
4; – 6; 2);
б)
![]() (2;
3; – 2);
(2;
3; – 2);
в)
![]() (4;
5; 1);
(4;
5; 1);
г)
![]() (–
1; 3; 2).
(–
1; 3; 2).
-
Укажите вектор, неколлинеарный вектору
 (1;
– 1; 2).
а)
(1;
– 1; 2).
а)
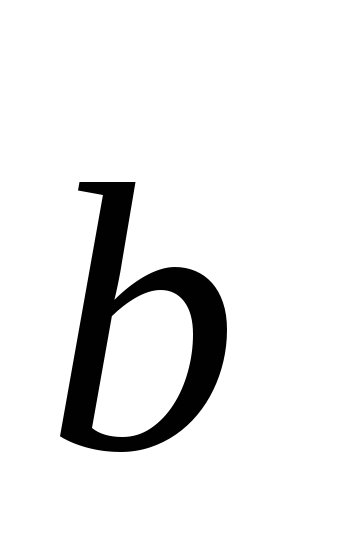 (2;
– 2; 4);
(2;
– 2; 4);
б)
![]() (2;
2; – 4);
(2;
2; – 4);
в)
![]() (–
3; 3; –
6);
(–
3; 3; –
6);
г)
![]()
![]() .
.
-
Даны точки А(3; 3; 3) и В(– 1; 5; 7). Найдите координаты середины отрезка АВ. а) (2; 8; 10);
б) (1; 4; 5);
в) (– 2; 1; 2);
г) (4; – 2; – 4).
-
Даны точки А(1; 5; 8) и В(5; – 3; 8). Найдите координаты середины отрезка АВ. а) (– 2; 4; 0);
б) (3; 1; 8);
в) (– 2; 4; 8);
г) (3; 1; 12).
-
Найдите скалярное произведение векторов
 (4;
– 2; 1) и
(4;
– 2; 1) и
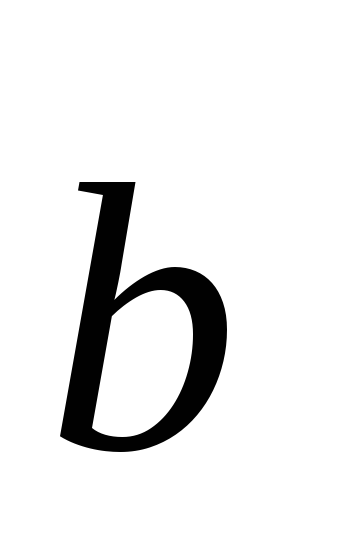 (1;
2; 3).
а)
3;
(1;
2; 3).
а)
3;
б) 5;
в) – 3;
г) 0.
-
Найдите скалярное произведение векторов
 (2;
3; – 4) и
(2;
3; – 4) и
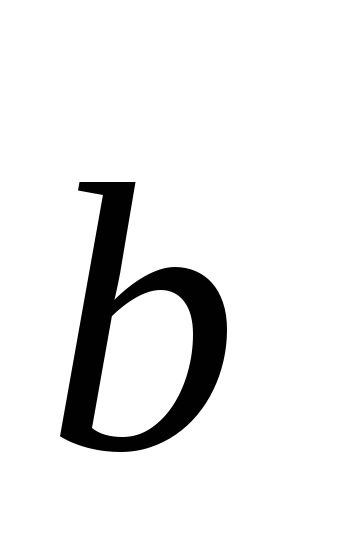 (1;
1; 1).
а) – 2;
(1;
1; 1).
а) – 2;
б) 0;
в) 4;
г) 1.
-
Укажите вектор, ортогональный вектору
 (3;
4).
а) (5; 1);
(3;
4).
а) (5; 1);
б) (– 3; – 4);
в) (– 4; 3);
г) (4; 3).
-
Укажите вектор, не ортогональный вектору
 (6;
– 2).
а)
(– 6; 2);
(6;
– 2).
а)
(– 6; 2);
б) (1; 3);
в) (2; 6);
г) (3; 9).
-
Укажите неверное утверждение:
а) арифметическим n-мерным вектором называется упорядоченный набор из n чисел;
б) если
![]() = (а1,
а2,…,
аn)
и
= (а1,
а2,…,
аn)
и
![]() = (b1,
b2,…,
bn),
то
= (b1,
b2,…,
bn),
то
![]() =
=
![]()
а1
= b1
а2
= b2
аn
= bn;
а1
= b1
а2
= b2
аn
= bn;
в) суммой
арифметических векторов
![]() = (а1,
а2,…,
аn)
и
= (а1,
а2,…,
аn)
и
![]() = (b1,
b2,…,
bn)
называется вектор
= (b1,
b2,…,
bn)
называется вектор
![]() +
+
![]() = (а1
+ b1,
а2
+ b2,
…, аn
+ bn);
= (а1
+ b1,
а2
+ b2,
…, аn
+ bn);
г)
произведением вектора
![]() = (а1,
а2,…,
аn)
на число
называется вектор
= (а1,
а2,…,
аn)
на число
называется вектор ![]() = (а1,
а2,…,
аn).
= (а1,
а2,…,
аn).
-
К эквивалентным системам векторов не приводят следующие элементарные преобразования:
а) умножение вектора системы на отличное от нуля число;
б) замена вектора системы суммой данного вектора с другим вектором системы;
в) удаление из системы (включение в систему) вектора, являющегося линейной комбинацией остальных векторов системы;
г) умножение вектора системы на нуль.
-
Рангом системы векторов называется:
а) число векторов в ее базисе;
б) число векторов в системе;
в) сумма векторов системы;
г) эквивалентная система векторов.
-
Укажите линейно независимую систему векторов:
а)
![]() = (2; 6),
= (2; 6),
![]() = (– 1; – 3);
= (– 1; – 3);
б)
![]() = (1; – 2),
= (1; – 2),
![]() = (– 2; 1);
= (– 2; 1);
в)
![]() = (0; – 3),
= (0; – 3),
![]() = (0; 5);
= (0; 5);
г)
![]() = (– 1; 4),
= (– 1; 4),
![]() = (– 3; 12).
= (– 3; 12).
-
Укажите линейно независимую систему векторов:
а)
![]() = (7; – 3),
= (7; – 3),
![]() = (– 1; 5);
= (– 1; 5);
б)
![]() = (2; 0),
= (2; 0),
![]() = (– 3; 0);
= (– 3; 0);
в)
![]() = (2; – 1),
= (2; – 1),
![]() = (6; – 3);
= (6; – 3);
г)
![]() = (0; 7),
= (0; 7),
![]() = (0; – 4).
= (0; – 4).
-
Найдите разложение вектора
 по векторам
по векторам
 и
и
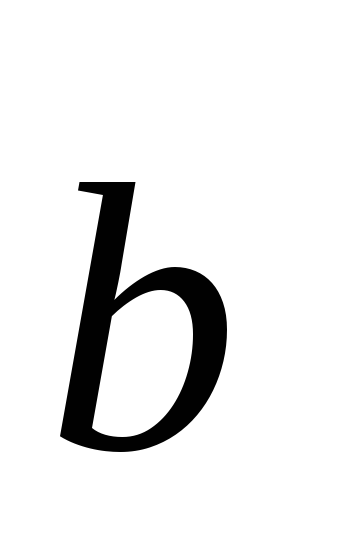 ,
если
,
если
 (–
4; 2),
(–
4; 2),
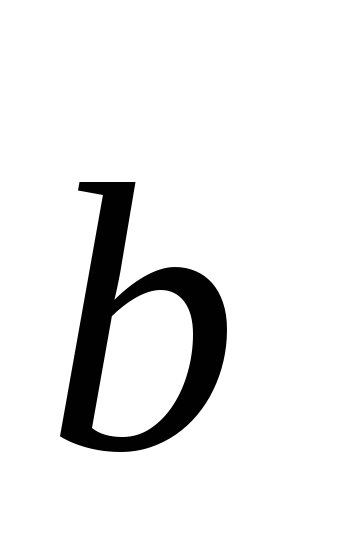 (3;
5),
(3;
5),
 (1;
– 7).
(1;
– 7).
а)
![]() =
=
![]() +
+
![]() ;
;
б)
![]() =
=
![]()
![]() +
+
![]() ;
;
в)
![]() =
=
![]() –
–
![]() ;
;
г)
![]() = –
= –![]() –
–
![]() .
.
