Эллипсоид

Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:

. (8)

Это уравнение называется каноническим уравнением эллипсоида.

Эллипсоид представляет собой замкнутую овальную поверхность, обладающую тремя взаимно перпендикулярными плоскостями симметрии.

Для построения эллипсоида в Ехсеl каноническое уравнение (8) необходимо разрешить относительно переменной z (представить в виде z=f(x,y)).

Задание 8. Построить верхнюю часть эллипсоида , лежащую в диапазонах: х[-4; 4], y[-3; 3] с шагом h=0.5 для обеих переменных.

Параболоид

Существует два вида параболоидов: эллиптические и гиперболические.

Эллиптическим параболоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением:

. (9)

Эллиптический параболоид имеет вид бесконечной выпуклой чаши. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной эллиптического параболоида; числа р и q называются его параметрами.

Гиперболическим параболоидом называется поверхность, определяемая уравнением

. (10)

Гиперболический параболоид имеет форму седла. Он обладает двумя взаимно перпендикулярными плоскостями симметрии. Точка, с которой совмещено начало координат, называется вершиной гиперболического параболоида: числа р и q называются его параметрами.

Задание 9. Построить эллиптический параболоид . Диапазон изменения переменных: х[-15; 15] с шагом h=0.5, y[-5; 5] с шагом h=1.

Задание 10. Построить гиперболический параболоид . Диапазон изменения переменных: х[-10; 10] с шагом h=0.5, y[-5; 5] с шагом h=1.

Конус второго порядка

Конусом второго порядка называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

. (11)

Конус образован прямыми линиями (образующими), проходящими через начало координат (вершина конуса). Сечение конуса плоскостью, не проходящей через начало координат, дает эллипс.

В Ехсе1 построение конуса второго порядка аналогично построению других поверхностей, рассмотренных ранее.

Задание 11. Построить нижнюю часть конуса . Диапазон изменения переменных: х[-10; 10] с шагом h=0.5, y[-7; 7] с шагом h=1.

Лабораторная работа №3 по теме «Матричные операции в Excel»

Цель работы: научиться использовать матричные функции MS Excel.

Матричные операции в Excel

1. Умножение матрицы на число. Матрицу умножить на число 9.

   1. Ввести матрицу А в диапазон А1:В2, число 9 в ячейку С1

   2. Выделить диапазон D1:E2 под новую матрицу

   3. В Строке формул набрать =С1*A1:B2

   4. Нажать, удерживая, комбинация клавиш Ctrl+Shift+Enter, в диапазоне D1:E2 появится матрица

2. Вычисление определителя матрицы. Вычислить определитель матрицы .

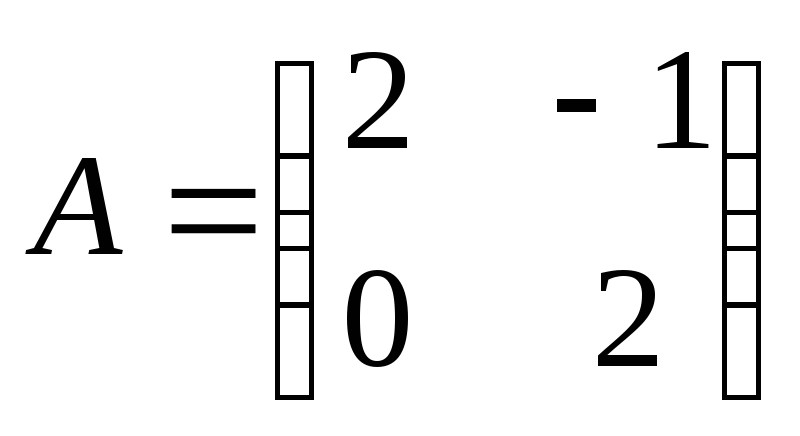   1. Ввести матрицу А в диапазон А1:В2

   2. Выделить ячейку G1

   3. В основном меню ВставкаФункция МатематическиеМОПРЕД

   4. В появившемся диалоговом окне при помощи мышки ввести диапазон A1:B2

   5. Нажать Enter, в ячейке G1 появится посчитанный определитель матрицы 4.

3. Сложение и вычитание матриц.

III.1. Даны матрицы и . Найти С=А+В.

1. Ввести матрицу А в диапазон А1:В2, ввести матрицу в диапазон D1:E2

2. Выделить диапазон G1:H2 под новую матрицу

3. В Строке формул набрать =A1:B2+D1:E2

4. Нажать, удерживая, комбинация клавиш Ctrl+Shift+Enter, в диапазоне G1:H2 появится матрица

III.2. Получить матрицу С, вычитанием матрицы из .

1. Ввести матрицу А в диапазон А1:В2, ввести матрицу B в диапазон D1:E2

2. В Строке формул при помощи мыши ввести =A1:B2-G1:H2

3. Нажать, удерживая, комбинация клавиш Ctrl+Shift+Enter, в диапазоне D1:E2 появится матрица

3. Нахождение обратной матрицы. Получить обратную матрицу A^-1, .

   1. Ввести матрицу А в диапазон А1:В2

   2. Выделить диапазон D4:E5 под новую матрицу

   3. В основном меню ВставкаФункцияМатематическиеМОБР

   4. В появившемся диалогом окне в поле Массив ввести диапазон А1:В2

   5. Нажать, удерживая, комбинация клавиш Ctrl+Shift+Enter, в диапазоне D4:E5 появится матрица

4. Умножение матриц. Получить матрицу С, умножив матрицы и , т.е. С=А*В.

   1. Ввести матрицу А в диапазон А1:В2, ввести матрицу В в диапазон D1:E2

   2. Выделить диапазон А4:В5 под новую матрицу

   3. В основном меню ВставкаФункция  МатематическиеМУМНОЖ

   4. В появившемся диалогом окне в поле Массив1 ввести диапазон А1:В2, в поле Массив2 ввести диапазон D1:E2

   5. Нажать, удерживая, комбинация клавиш Ctrl+Shift+Enter, в диапазоне A4:B5 появится матрица

Пример 3. Решить систему линейных алгебраических уравнений матричным методом: .

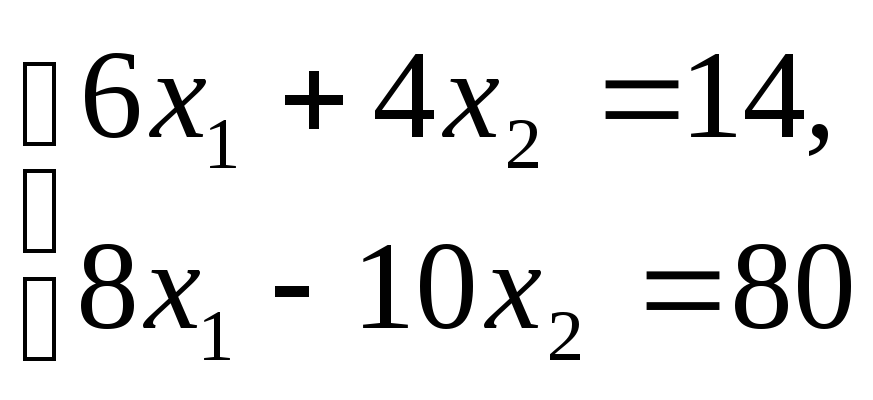Оформление на компьютере: