|
Четырехполюсником
называют
сколь угодно сложную электрическую
цепь, имеющую четыре внешних зажима,
через которые она может взаимодействовать
с внешними цепями. Трансформатор,
фильтр, линию электропередачи, мостовую
схему и т.д. можно рассматривать как
четырехполюсник. Теория четырехполюсников
позволяет устанавливать связи между
напряжениями, токами двух ветвей,
подключенных к четырем зажимам сколь
угодно сложной цепи, без исследования
режимов работы ее отдельных участков.Суть
теории заключается в следующем:1.
Пользуясь некоторыми обобщенными
параметрами четырехполюсника, можно
определять напряжения и токи на его
входе и выходе, не рассматривая
процессы, происходящие внутри
четырехполюсника.2.
Сложная электрическая цепь может быть
рассмотрена как совокупность
объединенных по определенной схеме
простейших четырехполюсников. Теория
четырехполюсников позволяет рассчитать
параметры такого составного
четырехполюсника при помощи параметров
входящих в него четырехполюсников.3.
Получаемые таким образом значения
электрических величин на входе и
выходе позволяют оценить режим работы
канала передачи в целом. При этом
обобщенные параметры четырехполюсника
позволяют сопоставить и правильно
оценить передающие свойства электрических
цепей, различных по своим свойствам
и структуре.4. Теория
четырехполюсников позволяет находить
структуру и элементы четырехполюсника
по заданным характеристикам, т.е.
решать задачу синтеза.
Классификация четырехполюсниковЧетырехполюсники
классифицируются по разным признакам.
Они могут быть активными и пассивными,
симметричными и несимметричными,
линейными и нелинейными, обратимыми
и необратимыми, эквивалентными и
неэквивалентными. Активные
четырехполюсники
— это четырехполюсники, которые
содержат ветви с нескомпенсированными
источниками энергии, при этом напряжение
на разомкнутых зажимах не равно нулю.
Пассивные
четырехполюсники
либо не содержат источников энергии,
либо, если они есть, то суммарное их
действие взаимно компенсируется
внутри четырехполюсника таким образом,
что напряжение на входных и выходных
зажимах равно нулю. В дальнейшем
рассматривается теория пассивных
четырехполюсников, т.к. активный
четырехполюсник может быть заменен
эквивалентным ему пассивным и вынесенным
за зажимы последнего эквивалентными
источниками ЭДС.Если четырехполюсник
симметричный,
то перемена
мест подключения входных и выходных
зажимов не изменит токораспределения
во внешней цепи.В линейных
четырехполюсниках связь между токами
и напряжениями имеет линейную
зависимость. В таких четырехполюсниках
нелинейные элементы (вольт-амперные
характеристики их имеют нелинейный
характер) отсутствуют. Обратимые
четырехполюсники
— это такие четырехполюсники, для
которых справедлив принцип взаимности
(отношение
напряжения на входе к току на выходе
не зависит от того, какая пара зажимов
выбрана в качестве входных).
Эквивалентные четырехполюсники — это
такие четырехполюсники, при взаимной
замене которых входные и выходные
токи и напряжения не изменятся.
Четырехполюсники также подразделяются
по схемам соединения входящих в них
элементов: Т,
П, Г-образные,
мостовые и
др.
|
Характеристические
параметры четырехполюсникаДля
несимметричных четырехполюсников
можно подобрать такую пару сопротивлений
и , для которых соблюдаются следующие
условия:1. Входное сопротивление
со стороны выводов 1—1 , если к
выводам 2—2 подключено
сопротивление 2. Входное
сопротивление со стороны
выводов 2—2 , если к выводам 1—1
подключено сопротивление и
называют характеристическими
сопротивлениями (характеристическими
параметрами) четырехполюсника.Третьим
характеристическим параметром
четырехполюсника является постоянная
передачи (или мера передачи),
которая характеризует четырехполюсник
как элемент, через который передается
мощность, и в общем случае представляет
собой комплексное число,где —
постоянная
ослабления,
— постоянная
фазы.
, называют вторичными
параметрами
четырехполюсника. Эти величины
независимы друг от друга и являются
функциями параметров четырехполюсника.
|
Последовательное
соединение индуктивно связанных
элементов цепи
а) б) б) а
- согласное включение; б - встречное
включениеРисунок 4.6 - Последовательное
соединение катушек индуктивностиЭквивалентная
индуктивность: а
- согласное включение; б - встречное
включениеРисунок 4.6 - Последовательное
соединение катушек индуктивностиЭквивалентная
индуктивность: . (4.11)<+>
- согласное, <-> - встречное.В идеальном
случае (k=1): . (4.11)<+>
- согласное, <-> - встречное.В идеальном
случае (k=1):
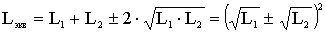 .Если,
кроме того, L1=L2,
то при согласном включении: .Если,
кроме того, L1=L2,
то при согласном включении:
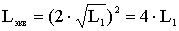 ,
встречном включении: ,
встречном включении:
 .Входное
сопротивление всей цепи: .Входное
сопротивление всей цепи:
 .
(4.12) .
(4.12)
|
|
Параллельное
соединение индуктивно связанных
элементов цепи
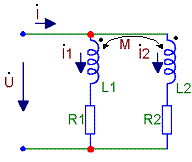 Рисунок
4.7 - Параллельное соединение катушек
индуктивностиВведем обозначения: Рисунок
4.7 - Параллельное соединение катушек
индуктивностиВведем обозначения:
 ; ;
 ; ; . .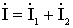 ; ;
 => =>
 => =>
 ;, ;,
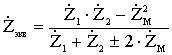 [одноименные
соединения]
(4.13)Вывод: при параллельном соединении
эквивалентное сопротивление меньше
меньшего из сопротивлений, однако
несколько больше эквивалентного
сопротивления при отсутствии взаимной
индукции - при одноименном соединении
и меньше - при разноименном. [одноименные
соединения]
(4.13)Вывод: при параллельном соединении
эквивалентное сопротивление меньше
меньшего из сопротивлений, однако
несколько больше эквивалентного
сопротивления при отсутствии взаимной
индукции - при одноименном соединении
и меньше - при разноименном.
|
RC-фильтрыУсилитель
с частотно-зависимым коэффициентом
усиления является активным фильтром.
ОУ является весьма подходящим элементом
для реализации подобных фильтров. Для
выбора типа цепей обратных связей
используется теория синтеза фильтров.
На
рис. 16 а,б представлены примеры ФНЧ
первого и второго порядков.
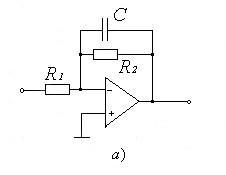  Рис.
16Обобщенные передаточные характеристики
фильтров равны соответственно Рис.
16Обобщенные передаточные характеристики
фильтров равны соответственно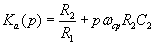
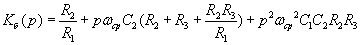 или или
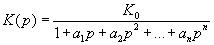 где
wcp--частота
среза, р-нормированная к w комплексная
частота. Выбором параметров схемы
можно реализовать фильтры Баттеворта,
Чебышева, Бесселя. Так, например, для
фильтра Баттерворта 1-го порядка должно
выполняться где
wcp--частота
среза, р-нормированная к w комплексная
частота. Выбором параметров схемы
можно реализовать фильтры Баттеворта,
Чебышева, Бесселя. Так, например, для
фильтра Баттерворта 1-го порядка должно
выполняться
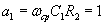 ,
а для фильтра Баттерворта 2-го порядка ,
а для фильтра Баттерворта 2-го порядка
 , ,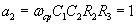 .Все
свойства фильтров различных типов
любого порядка (обычно до 10), значения
коэффициентов an рассчитаны и сведены
в таблицы, имеющиеся в руководствах
по проектированию фильтров. Для
построения активных фильтров высоких
частот в выражении (1) следует осуществить
замену р на 1/р. Соответственно, схема
ФВЧ получается из схемы ФНЧ взаимной
заменой R
и C
в цепях, определяющих частотную
характеристику. Так, схемы рис.16
приобретут вид рис.17 для ФВЧ. .Все
свойства фильтров различных типов
любого порядка (обычно до 10), значения
коэффициентов an рассчитаны и сведены
в таблицы, имеющиеся в руководствах
по проектированию фильтров. Для
построения активных фильтров высоких
частот в выражении (1) следует осуществить
замену р на 1/р. Соответственно, схема
ФВЧ получается из схемы ФНЧ взаимной
заменой R
и C
в цепях, определяющих частотную
характеристику. Так, схемы рис.16
приобретут вид рис.17 для ФВЧ.
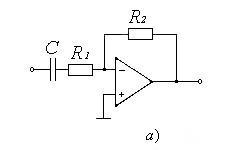 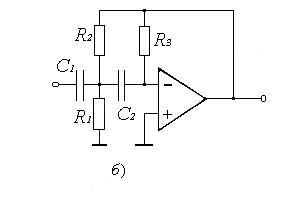 Рис.17Для
построения полосовых фильтров
осуществляют замену p
на Рис.17Для
построения полосовых фильтров
осуществляют замену p
на
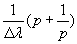 ,
где l-
нормированная относительно резонансной
частоты полоса пропускания фильтра.
Добротность фильтра определяется как ,
где l-
нормированная относительно резонансной
частоты полоса пропускания фильтра.
Добротность фильтра определяется как
 Передаточная
характеристика может быть записана
как, Передаточная
характеристика может быть записана
как,
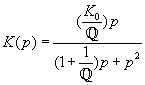 Где
К0-коэффициент
усиления на резонансной частоте.
Полосовой фильтр может быть реализован
в виде каскадного соединения ФНЧ и
ФВЧ, но может быть создан и на одном
ОУ, например, так, как показано на
рис.18. Где
К0-коэффициент
усиления на резонансной частоте.
Полосовой фильтр может быть реализован
в виде каскадного соединения ФНЧ и
ФВЧ, но может быть создан и на одном
ОУ, например, так, как показано на
рис.18.
 Рис.18Здесь Рис.18Здесь
 Отсюда
получаем Отсюда
получаем
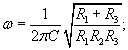 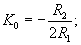  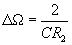
|
Лапласа
преобразование, преобразование,
переводящее функцию f (t) действительного
переменного t
(0 < t
< ¥), называемую "оригиналом", в
функцию
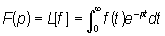 (1)комплексного
переменного р
=s +it. Под Л. п. понимают также не только
само преобразование, но и его результат
— функцию F
(p).
Интеграл в правой части формулы (1)
называется интегралом Лапласа. Он был
рассмотрен П. Лапласом
в ряде работ, которые объединены в его
книге "Аналитическая теория
вероятностей", вышедшей в 1812.
Значительно раньше (в 1737) такие интегралы
применял к решению дифференциальных
уравнений Л. Эйлер.При
некоторых условиях, указанных ниже,
Л. п. определяет функцию f
(t)
однозначно, в простейших случаях —
по формуле обращения: (1)комплексного
переменного р
=s +it. Под Л. п. понимают также не только
само преобразование, но и его результат
— функцию F
(p).
Интеграл в правой части формулы (1)
называется интегралом Лапласа. Он был
рассмотрен П. Лапласом
в ряде работ, которые объединены в его
книге "Аналитическая теория
вероятностей", вышедшей в 1812.
Значительно раньше (в 1737) такие интегралы
применял к решению дифференциальных
уравнений Л. Эйлер.При
некоторых условиях, указанных ниже,
Л. п. определяет функцию f
(t)
однозначно, в простейших случаях —
по формуле обращения: (2)Л.
п. является линейным функциональным
преобразованием. Из числа основных
формул Л. п. можно отметить следующие: (2)Л.
п. является линейным функциональным
преобразованием. Из числа основных
формул Л. п. можно отметить следующие: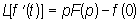 , ,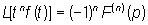 ,
n
= 1, 2, …, ,
n
= 1, 2, …, ,
t
>0.Л. п. в сочетании с формулой (2) его
обращения применяется к интегрированию
дифференциальных уравнений. В частности,
в силу свойства (1) и линейности, Л. п.
решения обыкновенного линейного
дифференциального уравнения с
постоянными коэффициентами удовлетворяет
алгебраическому уравнению 1-й степени
и может быть, следовательно, легко
найдено. Так, если, например, у’’
+ у = f
(t),
y (0)
= y’ (0)
= 0 и Y
(p)
= L [y], F (p)
= L [f], то
L [y’’] = p2Y
(p)
и p2Y
(p)
+ Y (p)
= F (p),
откуда ,
t
>0.Л. п. в сочетании с формулой (2) его
обращения применяется к интегрированию
дифференциальных уравнений. В частности,
в силу свойства (1) и линейности, Л. п.
решения обыкновенного линейного
дифференциального уравнения с
постоянными коэффициентами удовлетворяет
алгебраическому уравнению 1-й степени
и может быть, следовательно, легко
найдено. Так, если, например, у’’
+ у = f
(t),
y (0)
= y’ (0)
= 0 и Y
(p)
= L [y], F (p)
= L [f], то
L [y’’] = p2Y
(p)
и p2Y
(p)
+ Y (p)
= F (p),
откуда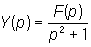 Многочисленные
задачи электротехники, гидродинамики,
механики, теплопроводности эффективно
решаются методами, использующими Л.
п.Л. п. нашло особенно широкое применение
в обосновании операционного
исчисления,
в котором обычно вместо Л. п. F (p) вводится
"изображение" оригинала f
(t)
— функция pF
(p).Современная
общая теория Л. п. строится на основе
интегрирования в смысле Лебега (см.
Интеграл).
Для применимости Л. п. к функции f
(t)
необходимо, чтобы f
(t)
была интегрируема в смысле Лебега на
любом конечном интервале (0, t), t
> 0 и
интеграл (1) для неё сходился хотя бы
в одной точке p0
= s0
+ it0.
Если интеграл (1) сходится в точке р0,
то он сходится во всех точках р, для
которых Re (р—р0)
> 0. Т. о., если интеграл (1) сходится
хотя бы в одной точке плоскости p0,
то либо он сходится во всей плоскости,
либо существует такое число sс,
что при Re p
> sc
интеграл (1) сходится, а при Re р
< sс
расходится. Число sс
называется абсциссой сходимости
интеграла Лапласа.
F (p)
— аналитическая
функция
в полуплоскости Re р
> sс. Многочисленные
задачи электротехники, гидродинамики,
механики, теплопроводности эффективно
решаются методами, использующими Л.
п.Л. п. нашло особенно широкое применение
в обосновании операционного
исчисления,
в котором обычно вместо Л. п. F (p) вводится
"изображение" оригинала f
(t)
— функция pF
(p).Современная
общая теория Л. п. строится на основе
интегрирования в смысле Лебега (см.
Интеграл).
Для применимости Л. п. к функции f
(t)
необходимо, чтобы f
(t)
была интегрируема в смысле Лебега на
любом конечном интервале (0, t), t
> 0 и
интеграл (1) для неё сходился хотя бы
в одной точке p0
= s0
+ it0.
Если интеграл (1) сходится в точке р0,
то он сходится во всех точках р, для
которых Re (р—р0)
> 0. Т. о., если интеграл (1) сходится
хотя бы в одной точке плоскости p0,
то либо он сходится во всей плоскости,
либо существует такое число sс,
что при Re p
> sc
интеграл (1) сходится, а при Re р
< sс
расходится. Число sс
называется абсциссой сходимости
интеграла Лапласа.
F (p)
— аналитическая
функция
в полуплоскости Re р
> sс.
|
|
Уравнения
передачи четырехполюсникаБудем
считать, что четырехполюсник (рис.
5.1) является линейным, а действующие
в нем сигналы - гармоническими. Любой
четырехполюсник характеризуется
четырьмя величинами: входным
напряжениемU1 и входным током I1, выходным
напряжением U2 и выходным током I2.
Уравнения, определяющие зависимость
между U1, U2, I1 и I2 называются уравнениями
передачи четырехполюсников.Только
две из этих величин являются независимыми.
Например, если подать на вход и выход
четырехполюсника напряжения U1 и U2, то
они создадут вполне определенные
входной I1 и выходной I2 токи. Поэтому
для линейного четырехполюсника можно
записать следующие два уравнения,
связывающие его входные и выходные
токи и напряжения:  ; ;
 Уравнения
(5.1) можно записать в матричной
форме: Уравнения
(5.1) можно записать в матричной
форме: (5.2) (5.2) Коэффициенты
Y11, Y12, Y21, Y22 в уравнениях (5.1) называются
Y-параметрами, а уравнения (5.1) называются
уравнениями передачи четырехполюсника
в Y-параметрах. Уравнения передачи
четырехполюсника в Z-параметрах: Коэффициенты
Y11, Y12, Y21, Y22 в уравнениях (5.1) называются
Y-параметрами, а уравнения (5.1) называются
уравнениями передачи четырехполюсника
в Y-параметрах. Уравнения передачи
четырехполюсника в Z-параметрах: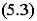  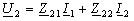 или
в матричной форме: или
в матричной форме: .
(5.4)Уравнения передачи
четырехполюсника в Н-параметрах: .
(5.4)Уравнения передачи
четырехполюсника в Н-параметрах:  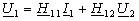 ; ;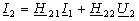 или
в матричной форме: или
в матричной форме: .
(5.6)Уравнения передачи
четырехполюсника в A-параметрах: .
(5.6)Уравнения передачи
четырехполюсника в A-параметрах: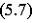  ; ;
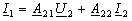 или
в матричной форме: или
в матричной форме: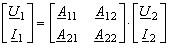 .
(5.8) Все формы передачи уравнений
равноправны. Выбор той или иной формы
зависит от задачи, которая в данном
случае решается. Уравнения передачи
вH-параметрах и Y -параметрах широко
используются, например, при расчетах
транзисторных схем. Эти параметры
приводятся в справочной литературе
по транзисторам, или могут быть
определены по их входным и выходным
характеристикам.Все системы
параметров-коэффициентов описывают
один и тот же четырехполюсник, поэтому
между ними существует однозначная
взаимосвязь.Физический смысл
параметров-коэффициентов. Для выяснения
физического смысла необходимо
четырехполюсник поставить в такой
режим работы, при котором в уравнениях
передачи будет содержаться только
один параметр, который нас интересует,
например,Z11 . Эти условия будут созданы,
если четырехполюсник перевести в
режим холостого хода (зажимы разомкнуты)
или короткого замыкания (зажимы
замкнуты).Переведем четырехполюсник
в режим короткого замыкания (КЗ) по
выходу, т.е. замкнем зажимы (2-2). В этом
случае U2 = 0 и уравнения (5.1) примут
вид: .
(5.8) Все формы передачи уравнений
равноправны. Выбор той или иной формы
зависит от задачи, которая в данном
случае решается. Уравнения передачи
вH-параметрах и Y -параметрах широко
используются, например, при расчетах
транзисторных схем. Эти параметры
приводятся в справочной литературе
по транзисторам, или могут быть
определены по их входным и выходным
характеристикам.Все системы
параметров-коэффициентов описывают
один и тот же четырехполюсник, поэтому
между ними существует однозначная
взаимосвязь.Физический смысл
параметров-коэффициентов. Для выяснения
физического смысла необходимо
четырехполюсник поставить в такой
режим работы, при котором в уравнениях
передачи будет содержаться только
один параметр, который нас интересует,
например,Z11 . Эти условия будут созданы,
если четырехполюсник перевести в
режим холостого хода (зажимы разомкнуты)
или короткого замыкания (зажимы
замкнуты).Переведем четырехполюсник
в режим короткого замыкания (КЗ) по
выходу, т.е. замкнем зажимы (2-2). В этом
случае U2 = 0 и уравнения (5.1) примут
вид: ,откуда ,откуда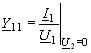 ; ; 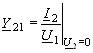 ,где
Y11 и Y21 – входная и взаимная (передаточная)
проводимости четырехполюсника при
КЗ выхода.Переведем четырехполюсник
в режим КЗ по входу, т.е. замкнем зажимы
(1-1). В этом случае U1 = 0 и уравнения (5.1)
примут вид: ,где
Y11 и Y21 – входная и взаимная (передаточная)
проводимости четырехполюсника при
КЗ выхода.Переведем четырехполюсник
в режим КЗ по входу, т.е. замкнем зажимы
(1-1). В этом случае U1 = 0 и уравнения (5.1)
примут вид: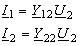 ,откуда ,откуда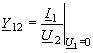
 ,где
Y12 и Y22 – взаимная (передаточная) и
выходная проводимости четырехполюсника
при КЗ входных зажимов.Переводя
четырехполюсник поочередно в режим
холостого хода (ХХ) на зажимах (2-2) и
(1-1) будем иметь то I2 = 0, то I1 = 0 и на
основании уравнений (5.3) получим: ,где
Y12 и Y22 – взаимная (передаточная) и
выходная проводимости четырехполюсника
при КЗ входных зажимов.Переводя
четырехполюсник поочередно в режим
холостого хода (ХХ) на зажимах (2-2) и
(1-1) будем иметь то I2 = 0, то I1 = 0 и на
основании уравнений (5.3) получим:


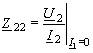
 где
Z11, Z21 - входное и взаимное (передаточное)
сопротивления четырехполюсника при
холостом ходе на входных зажимах
(2-2);Z22, Z12 – выходное и взаимное
(передаточное) сопротивления
четырехполюсника при холостом ходе
на зажимах (1-1).Рассуждая аналогичным
образом можно установить,
что:параметры A11 и A22 являются
безразмерными;параметр А12 имеет
размерность сопротивления;параметр
А21 имеет размерность проводимости;параметры
Н12 и Н21 являются безразмерными;параметры
Н11 и Н22 имеют размерность сопротивления
и проводимости соответственно. где
Z11, Z21 - входное и взаимное (передаточное)
сопротивления четырехполюсника при
холостом ходе на входных зажимах
(2-2);Z22, Z12 – выходное и взаимное
(передаточное) сопротивления
четырехполюсника при холостом ходе
на зажимах (1-1).Рассуждая аналогичным
образом можно установить,
что:параметры A11 и A22 являются
безразмерными;параметр А12 имеет
размерность сопротивления;параметр
А21 имеет размерность проводимости;параметры
Н12 и Н21 являются безразмерными;параметры
Н11 и Н22 имеют размерность сопротивления
и проводимости соответственно.
|
Операторный
метод анализа переходных процессов.Поскольку
для операторных токов, напряжений и
сопротивлений справедливы законы Ома
и Кирхгофа, то расчет операторных
токов и напряжений будет аналогичным
расчету постоянных токов и напряжений
в резистивных цепях постоянного тока.
В частности, могут быть использованы
все известные методы расчета (метод
эквивалентных преобразований, метод
узловых напряжений и т.д.), которые
основаны на законах Ома и Кирхгофа.
Учитывая изложенное, приведем методику
решения задач операторным
методом.1.Определяются начальные
условия
 и и
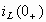 обычным
путем на основании законов коммутации.2.Для
цепи после коммутации составляется
операторная схема замещения, в которой
элементы представляются их операторными
схемами замещения, реальные токи и
напряжения заменяются операторными.
Такой замене подвергаются как искомые
токи и напряжения, так и известные
токи и напряжения источников.3.Для
операторной схемы замещения определяются
искомые операторные токи и напряжения
с использованием законов Ома, Кирхгофа
и всех методов расчета (эквивалентных
преобразований, эквивалентного
генератора, узловых напряжений и
т.д.).4.По найденным операторным токам
и напряжениям определяются реальные
токи и напряжения по таблицам или по
формуле разложения, которая будет
рассмотрена ниже.Необходимо отметить,
что при расчете переходных процессов
операторным методом мы будем иметь
дело с алгебраическими операциями
над простейшими функциями переменного
“р”
каковыми являются операторные
сопротивления и операторные функции
источников.Для практических целей
при анализе переходных процессов в
любой схеме классическим методом
может быть рекомендован следующий
алгоритм.1.Рассчитать принужденный
(установившийся) режим при t→∞.
Определить принужденные токи и
напряжения.2.Рассчитать режим до
коммутации. Определить токи в ветвях
с индуктивностью и напряжения на
конденсаторах. Значения этих величин
в момент коммутации является независимыми
начальными условиями.3.Составить
дифференциальные уравнения для
свободного процесса (Е = 0) в схеме
после коммутации по законам Кирхгофа
или по методу контурных токов.
Алгебраизировать данные уравнения,
получить характеристическое уравнение
и найти его корни. Существуют приемы,
упрощающие операцию отыскания корней
характеристического уравнения,
например, приравнивание нулю входного
операторного сопротивления цепи,
которое получается путем замены в
выражении комплексного сопротивления
цепи множителя "jω" на оператор
"р". 4.Записать общие выражения
для искомых напряжений и токов в
соответствии с видом корней
характеристического уравнения.
5.Переписать величины, полученные в
п. 4, и производные от них при t = 0.
6.Определить необходимые зависимые
начальные условия, используя независимые
начальные условия.7.Подставив начальные
условия в уравнения п. 5, найти
постоянные интегрирования. 8.Записать
законы изменения искомых токов и
напряжений. обычным
путем на основании законов коммутации.2.Для
цепи после коммутации составляется
операторная схема замещения, в которой
элементы представляются их операторными
схемами замещения, реальные токи и
напряжения заменяются операторными.
Такой замене подвергаются как искомые
токи и напряжения, так и известные
токи и напряжения источников.3.Для
операторной схемы замещения определяются
искомые операторные токи и напряжения
с использованием законов Ома, Кирхгофа
и всех методов расчета (эквивалентных
преобразований, эквивалентного
генератора, узловых напряжений и
т.д.).4.По найденным операторным токам
и напряжениям определяются реальные
токи и напряжения по таблицам или по
формуле разложения, которая будет
рассмотрена ниже.Необходимо отметить,
что при расчете переходных процессов
операторным методом мы будем иметь
дело с алгебраическими операциями
над простейшими функциями переменного
“р”
каковыми являются операторные
сопротивления и операторные функции
источников.Для практических целей
при анализе переходных процессов в
любой схеме классическим методом
может быть рекомендован следующий
алгоритм.1.Рассчитать принужденный
(установившийся) режим при t→∞.
Определить принужденные токи и
напряжения.2.Рассчитать режим до
коммутации. Определить токи в ветвях
с индуктивностью и напряжения на
конденсаторах. Значения этих величин
в момент коммутации является независимыми
начальными условиями.3.Составить
дифференциальные уравнения для
свободного процесса (Е = 0) в схеме
после коммутации по законам Кирхгофа
или по методу контурных токов.
Алгебраизировать данные уравнения,
получить характеристическое уравнение
и найти его корни. Существуют приемы,
упрощающие операцию отыскания корней
характеристического уравнения,
например, приравнивание нулю входного
операторного сопротивления цепи,
которое получается путем замены в
выражении комплексного сопротивления
цепи множителя "jω" на оператор
"р". 4.Записать общие выражения
для искомых напряжений и токов в
соответствии с видом корней
характеристического уравнения.
5.Переписать величины, полученные в
п. 4, и производные от них при t = 0.
6.Определить необходимые зависимые
начальные условия, используя независимые
начальные условия.7.Подставив начальные
условия в уравнения п. 5, найти
постоянные интегрирования. 8.Записать
законы изменения искомых токов и
напряжений.
|
Классический
метод анализа переходных процессовПри
анализе процессов в электрических
цепях приходится иметь дело с двумя
режимами работы установившемся
(стационарном) и переходным
(динамическим). В предыдущих главах
мы рассматривали цепи в установившемся
режиме, когда все параметры цепи либо
постоянны во времени, либо постоянны
по амплитуде токи и напряжения. Подобный
режим называется установившимся
(вынужденным). Принято также считать,
что в установившемся режиме находится
электрические цепи, еще не подключавшиеся
к источнику электрического сигнала,
т.е. цепь, в ветвях которой нет
токов.Переходным процессом называется
процесс перехода цепи от одного
установившегося режима к
другому.Возникновение режима
нестационарных переходных колебаний
в цепи может быть вызвано включением,
переключением, изменением параметров
цепи, т.е. обусловлено коммутацией в
цепи. В таком переходном состоянии
цепь называется динамической.Коммутация
обычно осуществляется с помощью
идеального ключа (рис. 4.1.1). Ключ это
двухполюсник с сопротивлением равным
 Рис.
4.1.1 Рис.
4.1.1
|
|
Графические
методы расчета
При использовании этих методов задача
решается путем графических построений
на плоскости. При этом характеристики
всех ветвей цепи следует записать в
функции одного общего аргумента.
Благодаря этому система уравнений
сводится к одному нелинейному уравнению
с одним неизвестным. Формально при
расчете различают цепи с последовательным,
параллельным и смешанным соединениями.
а) Цепи с последовательным соединением
резистивных элементов. При последовательном
соединении нелинейных резисторов в
качестве общего аргумента принимается
ток, протекающий через последовательно
соединенные элементы. Расчет проводится
в следующей последовательности. По
заданным ВАХ
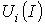 отдельных
резисторов в системе декартовых
координат отдельных
резисторов в системе декартовых
координат
 строится
результирующая зависимость строится
результирующая зависимость
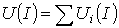 .
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью .
Затем на оси напряжений откладывается
точка, соответствующая в выбранном
масштабе заданной величине напряжения
на входе цепи, из которой восстанавливается
перпендикуляр до пересечения с
зависимостью
 .
Из точки пересечения перпендикуляра
с кривой .
Из точки пересечения перпендикуляра
с кривой
 опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей опускается
ортогональ на ось токов – полученная
точка соответствует искомому току в
цепи, по найденному значению которого
с использованием зависимостей
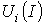 определяются
напряжения определяются
напряжения
 на
отдельных резистивных элементах.
Применение указанной методики
иллюстрируют графические построения
на рис. 2,б, соответствующие цепи на
рис. 2,а. на
отдельных резистивных элементах.
Применение указанной методики
иллюстрируют графические построения
на рис. 2,б, соответствующие цепи на
рис. 2,а.
 Графическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом
пересечений. В
этом случае один из нелинейных
резисторов, например, с ВАХ Графическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом
пересечений. В
этом случае один из нелинейных
резисторов, например, с ВАХ
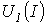 на
рис.2,а, считается внутренним
сопротивлением источника с ЭДС Е, а
другой – нагрузкой. Тогда на основании
соотношения на
рис.2,а, считается внутренним
сопротивлением источника с ЭДС Е, а
другой – нагрузкой. Тогда на основании
соотношения
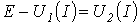 точка
а (см. рис. 3) пересечения кривых точка
а (см. рис. 3) пересечения кривых
 и и
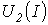 определяет
режим работы цепи. Кривая определяет
режим работы цепи. Кривая
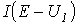 строится
путем вычитания абсцисс ВАХ строится
путем вычитания абсцисс ВАХ
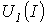 из
ЭДС Е для различных значений тока.
Использование данного метода наиболее
рационально при последовательном
соединении линейного и нелинейного
резисторов. В этом случае линейный
резистор принимается за внутреннее
сопротивление источника, и линейная
ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением
резистивных элементов. При параллельном
соединении нелинейных резисторов в
качестве общего аргумента принимается
напряжение, приложенное к параллельно
соединенным элементам. Расчет проводится
в следующей последовательности. По
заданным ВАХ из
ЭДС Е для различных значений тока.
Использование данного метода наиболее
рационально при последовательном
соединении линейного и нелинейного
резисторов. В этом случае линейный
резистор принимается за внутреннее
сопротивление источника, и линейная
ВАХ последнего строится по двум точкам.
б) Цепи с параллельным соединением
резистивных элементов. При параллельном
соединении нелинейных резисторов в
качестве общего аргумента принимается
напряжение, приложенное к параллельно
соединенным элементам. Расчет проводится
в следующей последовательности. По
заданным ВАХ
 отдельных
резисторов в системе декартовых
координат отдельных
резисторов в системе декартовых
координат
 строится
результирующая зависимость строится
результирующая зависимость
 .
Затем на оси токов откладывается
точка, соответствующая в выбранном
масштабе заданной величине тока
источника на входе цепи (при наличии
на входе цепи источника напряжения
задача решается сразу путем восстановления
перпендикуляра из точки, соответствующей
заданному напряжению источника, до
пересечения с ВАХ .
Затем на оси токов откладывается
точка, соответствующая в выбранном
масштабе заданной величине тока
источника на входе цепи (при наличии
на входе цепи источника напряжения
задача решается сразу путем восстановления
перпендикуляра из точки, соответствующей
заданному напряжению источника, до
пересечения с ВАХ
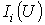 ),
из которой восстанавливается
перпендикуляр до пересечения с
зависимостью ),
из которой восстанавливается
перпендикуляр до пересечения с
зависимостью
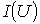 .
Из точки пересечения перпендикуляра
с кривой .
Из точки пересечения перпендикуляра
с кривой
 опускается
ортогональ на ось напряжений –
полученная точка соответствует
напряжению на нелинейных резисторах,
по найденному значению которого с
использованием зависимостей опускается
ортогональ на ось напряжений –
полученная точка соответствует
напряжению на нелинейных резисторах,
по найденному значению которого с
использованием зависимостей
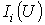 определяются
токи определяются
токи
 в
ветвях с отдельными резистивными
элементами. Использование данной
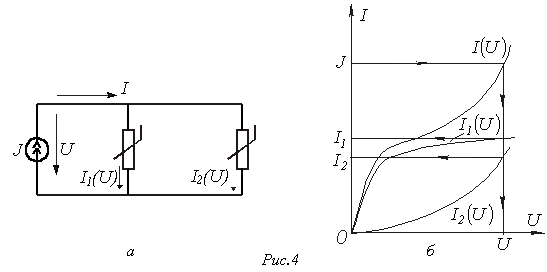
методики иллюстрируют графические
построения на рис. 4,б, соответствующие
цепи на рис. 4,а. в
ветвях с отдельными резистивными
элементами. Использование данной
методики иллюстрируют графические
построения на рис. 4,б, соответствующие
цепи на рис. 4,а.
 в) Цепи с
последовательно-параллельным
(смешанным) соединением резистивных
элементов. 1. Расчет таких цепей
производится в следующей последовательности:
Исходная схема сводится к цепи с
последовательным соединением
резисторов, для чего строится
результирующая ВАХ параллельно
соединенных элементов, как это показано
в пункте б). 2. Проводится расчет
полученной схемы с последовательным
соединением резистивных элементов
(см. пункт а), на основании которого
затем определяются токи в исходных
параллельных ветвях.
в) Цепи с
последовательно-параллельным
(смешанным) соединением резистивных
элементов. 1. Расчет таких цепей
производится в следующей последовательности:
Исходная схема сводится к цепи с
последовательным соединением
резисторов, для чего строится
результирующая ВАХ параллельно
соединенных элементов, как это показано
в пункте б). 2. Проводится расчет
полученной схемы с последовательным
соединением резистивных элементов
(см. пункт а), на основании которого
затем определяются токи в исходных
параллельных ветвях.
|
Спектры
простейших периодических сигналов.Пример
1.
Рассмотрим периодический сигнал,
заданный в виде усеченного ряда
Фурье: Спектр
амплитуд и спектр фаз этого сигнала
можно представить графически в виде
отрезков линий при соответствующих
значениях частоты. Длина каждой такой
линии пропорциональна амплитуде Ак
(для спектра амплитуд) или начальной
фазе φк
(для
спектра фаз) гармонической составляющей
с частотой к·ω1
(к=0,1,2…)
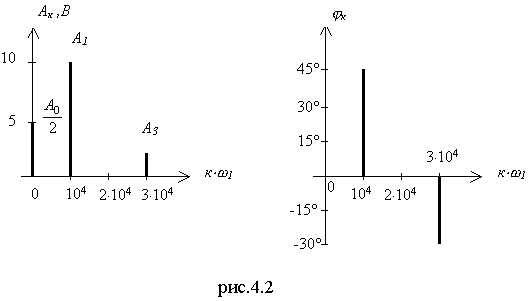
(рис.4.2). Спектр
амплитуд и спектр фаз этого сигнала
можно представить графически в виде
отрезков линий при соответствующих
значениях частоты. Длина каждой такой
линии пропорциональна амплитуде Ак
(для спектра амплитуд) или начальной
фазе φк
(для
спектра фаз) гармонической составляющей
с частотой к·ω1
(к=0,1,2…)
(рис.4.2).
 Пример
2. Рассмотрим
спектр последовательности видеоимпульсов
прямоугольной формы, изображенной на
рис.4.1. Для этого воспользуемся
соотношением (4.2), в котором необходимо
положить верхний предел интегрирования
равным tи,
а f(t)=Uо: Пример
2. Рассмотрим
спектр последовательности видеоимпульсов
прямоугольной формы, изображенной на
рис.4.1. Для этого воспользуемся
соотношением (4.2), в котором необходимо
положить верхний предел интегрирования
равным tи,
а f(t)=Uо:
 Поскольку
ω1Т=2π,
а Поскольку
ω1Т=2π,
а
 то
окончательно получим: то
окончательно получим: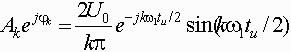 Введем
в рассмотрение скважность
последовательности Q=Т/tи.Тогда
ω1tи
= 2π/Q,
а спектр амплитуд и спектр фаз будут
иметь следующий вид: Введем
в рассмотрение скважность
последовательности Q=Т/tи.Тогда
ω1tи
= 2π/Q,
а спектр амплитуд и спектр фаз будут
иметь следующий вид: ; ;
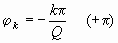 .(4.3)Значение
спектра фаз увеличивается на π
рад при частотах к·ω1,
на которых sin(p
/ Q)
меняет знак.Спектры амплитуд и фаз
для последовательности прямоугольных
импульсов при Q=2
изображены на рис.4.3 по значениям, .(4.3)Значение
спектра фаз увеличивается на π
рад при частотах к·ω1,
на которых sin(p
/ Q)
меняет знак.Спектры амплитуд и фаз
для последовательности прямоугольных
импульсов при Q=2
изображены на рис.4.3 по значениям,

|
Амплиту́дная
модуляция —
вид модуляции,
при которой изменяемым параметром
несущего
сигнала
является его амплитуда.ОпределениеПустьS(t) —
информационный сигнал, |
S(t)
| < 1,Uc(t) —
несущее колебание.Тогда
амплитудно-модулированный сигнал
Uam(t)
может быть записан следующим
образом: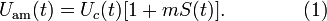 Здесь
m —
некоторая константа, называемая
коэффициентом модуляции. Формула (1)
описывает несущий сигнал Uc(t),
модулированный по амплитуде сигналом
S(t)
с коэффициентом модуляции m.
Предполагается также, что выполнены
условия: Здесь
m —
некоторая константа, называемая
коэффициентом модуляции. Формула (1)
описывает несущий сигнал Uc(t),
модулированный по амплитуде сигналом
S(t)
с коэффициентом модуляции m.
Предполагается также, что выполнены
условия: Выполнение
условий (2) необходимо для того, чтобы
выражение в квадратных скобках в (1)
всегда было положительным. Если оно
может принимать отрицательные значения
в какой-то момент времени, то происходит
так называемая перемодуляция
(избыточная модуляция). Простые
демодуляторы (типа квадратичного
детектора)
демодулируют такой сигнал с сильными
искажениями.Пример Выполнение
условий (2) необходимо для того, чтобы
выражение в квадратных скобках в (1)
всегда было положительным. Если оно
может принимать отрицательные значения
в какой-то момент времени, то происходит
так называемая перемодуляция
(избыточная модуляция). Простые
демодуляторы (типа квадратичного
детектора)
демодулируют такой сигнал с сильными
искажениями.Пример
 Спектр
АМ колебанияДопустим, что мы хотим
промодулировать несущее колебание
моногармоническим сигналом. Выражение
для несущего колебания с частотой ωc,
начальную фазу положим равной нулю,
имеет видUc(t)
= Csin(ωct).Выражение
для синусоидального сигнала с частотой
ωs
(сигнал подлежащий передаче) имеет
вид Спектр
АМ колебанияДопустим, что мы хотим
промодулировать несущее колебание
моногармоническим сигналом. Выражение
для несущего колебания с частотой ωc,
начальную фазу положим равной нулю,
имеет видUc(t)
= Csin(ωct).Выражение
для синусоидального сигнала с частотой
ωs
(сигнал подлежащий передаче) имеет
вид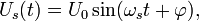 где где
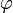 —
начальная фаза. Тогда, в соответствии
с (1) —
начальная фаза. Тогда, в соответствии
с (1) Приведённая
выше формула для y(t)
может быть записана в следующем
виде: Приведённая
выше формула для y(t)
может быть записана в следующем
виде: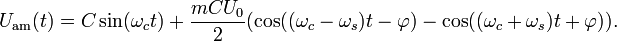 Радиосигнал
состоит из несущего колебания и двух
синусоидальных колебаний, называемых
боковыми
полосами,
каждое из которых имеет частоту немного
отличную от ωc.
Для синусоидального сигнала,
использованного здесь, частоты равны
ωc
+ ωs
и ωc
− ωs.
Пока несущие частоты соседних
радиостанций достаточно разнесены,
и боковые полосы не перекрываются
между собой, станции не будут влиять
друг на друга. Радиосигнал
состоит из несущего колебания и двух
синусоидальных колебаний, называемых
боковыми
полосами,
каждое из которых имеет частоту немного
отличную от ωc.
Для синусоидального сигнала,
использованного здесь, частоты равны
ωc
+ ωs
и ωc
− ωs.
Пока несущие частоты соседних
радиостанций достаточно разнесены,
и боковые полосы не перекрываются
между собой, станции не будут влиять
друг на друга.
|


 Рисунок
4.7 - Параллельное соединение катушек
индуктивностиВведем обозначения:
Рисунок
4.7 - Параллельное соединение катушек
индуктивностиВведем обозначения: =>
=>

 Рис.
16Обобщенные передаточные характеристики
фильтров равны соответственно
Рис.
16Обобщенные передаточные характеристики
фильтров равны соответственно Рис.17Для
построения полосовых фильтров
осуществляют замену p
на
Рис.17Для
построения полосовых фильтров
осуществляют замену p
на
 Рис.
4.1.1
Рис.
4.1.1 Графическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом
пересечений. В
этом случае один из нелинейных
резисторов, например, с ВАХ
Графическое
решение для последовательной нелинейной
цепи с двумя резистивными элементами
может быть проведено и другим методом
– методом
пересечений. В
этом случае один из нелинейных
резисторов, например, с ВАХ
 в) Цепи с
последовательно-параллельным
(смешанным) соединением резистивных
элементов. 1. Расчет таких цепей
производится в следующей последовательности:
Исходная схема сводится к цепи с
последовательным соединением
резисторов, для чего строится
результирующая ВАХ параллельно
соединенных элементов, как это показано
в пункте б). 2. Проводится расчет
полученной схемы с последовательным
соединением резистивных элементов
(см. пункт а), на основании которого
затем определяются токи в исходных
параллельных ветвях.
в) Цепи с
последовательно-параллельным
(смешанным) соединением резистивных
элементов. 1. Расчет таких цепей
производится в следующей последовательности:
Исходная схема сводится к цепи с
последовательным соединением
резисторов, для чего строится
результирующая ВАХ параллельно
соединенных элементов, как это показано
в пункте б). 2. Проводится расчет
полученной схемы с последовательным
соединением резистивных элементов
(см. пункт а), на основании которого
затем определяются токи в исходных
параллельных ветвях.
 Пример
2. Рассмотрим
спектр последовательности видеоимпульсов
прямоугольной формы, изображенной на
рис.4.1. Для этого воспользуемся
соотношением (4.2), в котором необходимо
положить верхний предел интегрирования
равным tи,
а f(t)=Uо:
Пример
2. Рассмотрим
спектр последовательности видеоимпульсов
прямоугольной формы, изображенной на
рис.4.1. Для этого воспользуемся
соотношением (4.2), в котором необходимо
положить верхний предел интегрирования
равным tи,
а f(t)=Uо: 
 Спектр
АМ колебанияДопустим, что мы хотим
промодулировать несущее колебание
моногармоническим сигналом. Выражение
для несущего колебания с частотой ωc,
начальную фазу положим равной нулю,
имеет видUc(t)
= Csin(ωct).Выражение
для синусоидального сигнала с частотой
ωs
(сигнал подлежащий передаче) имеет
вид
Спектр
АМ колебанияДопустим, что мы хотим
промодулировать несущее колебание
моногармоническим сигналом. Выражение
для несущего колебания с частотой ωc,
начальную фазу положим равной нулю,
имеет видUc(t)
= Csin(ωct).Выражение
для синусоидального сигнала с частотой
ωs
(сигнал подлежащий передаче) имеет
вид