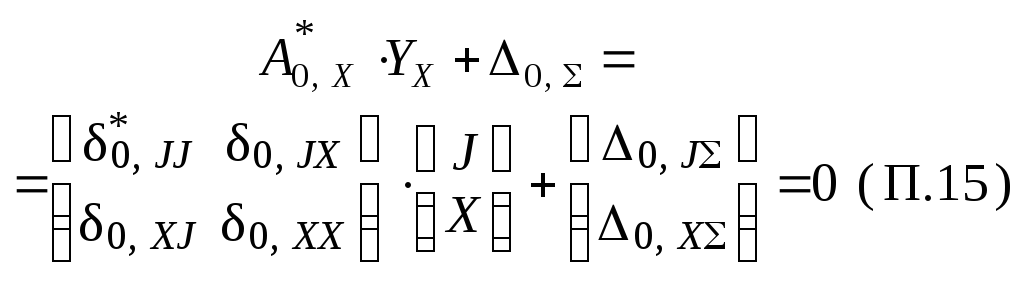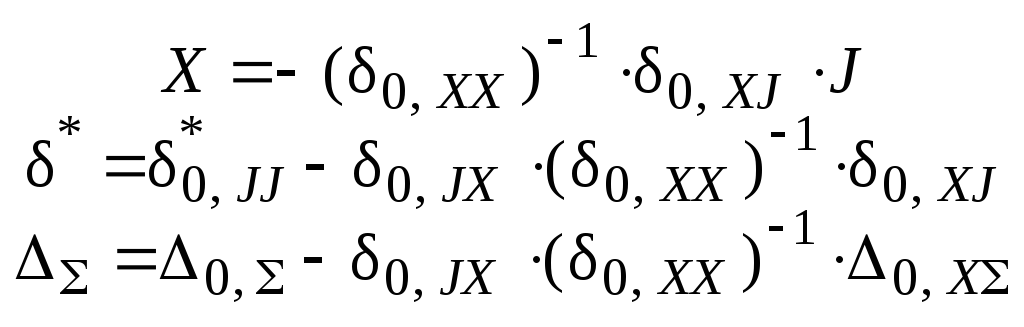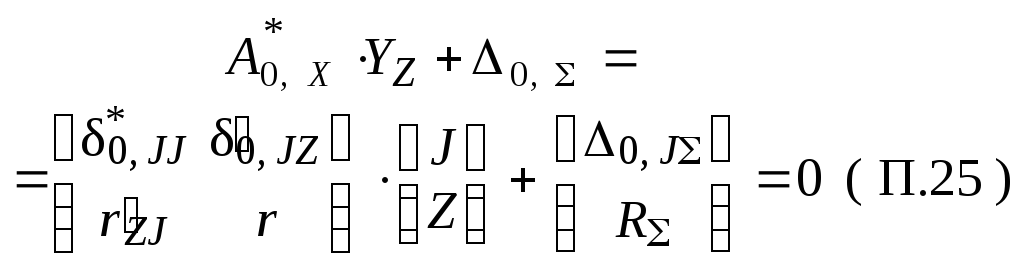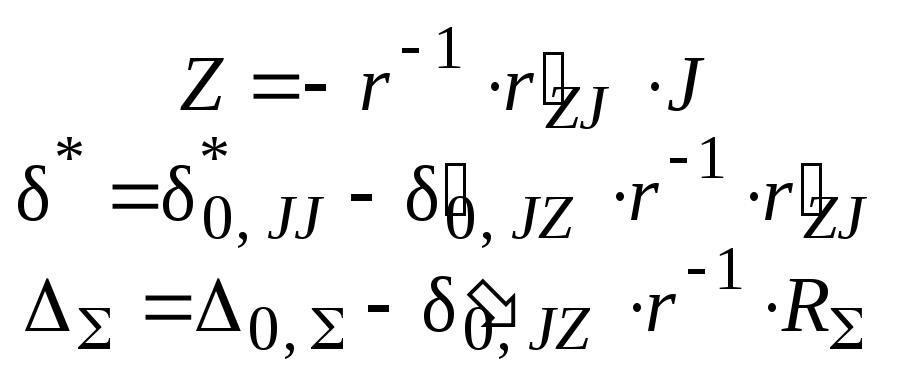4.Задания, приложение, библ

Независимо от общего числа неизвестных n₀ порядок уравнения ( П.9 ) относительно собственного числа  равен числу степеней свобо-ды n, так как  входит лишь в n диагональных компонентов матри-цы . После отыскания корней ( П.9 ) с помощью процедуры, опи-санной в п. 1.5.4, для каждого_j вычисляется собственный вектор основ-

ных неизвестных _{Y (j)}, первые n компонентов которого представляют собой собственный вектор сил инерции_J(j). Дальнейшее – определе-ние собственных векторов перемещений масс _y(j), проверка ортого-нальности главных форм и т.д. – выполняется так же, как в п. п. 1.5.4.

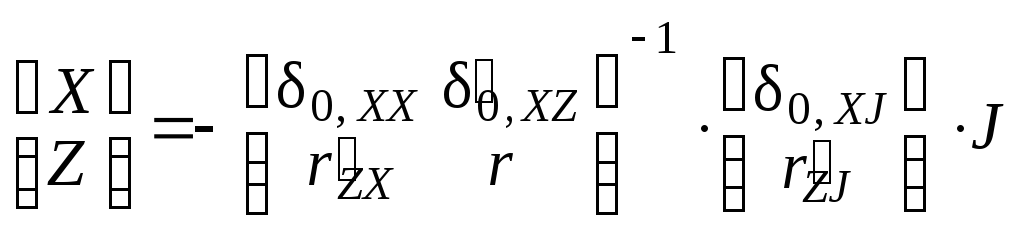, ( П.10 )

В расчёте на собственные колебания неизвестные Х и Z сами по себе не представляют интереса, поэтому после формирования системы уравнений ( П.8 ) из нее целесообразно исключить Х и Z, выразив их через J:

после чего вместо ( П.8 ) получаем систему уравнений с одними лишь неизвестными J, то есть ( 1.51 ) – для заданной системы, причем матри-

ца вычисляется через блоки матрицы :

. ( П.11 )

Так же можно поступать и с уравнениями установившихся вынуж-денных колебаний ( П.5 ), которые дают

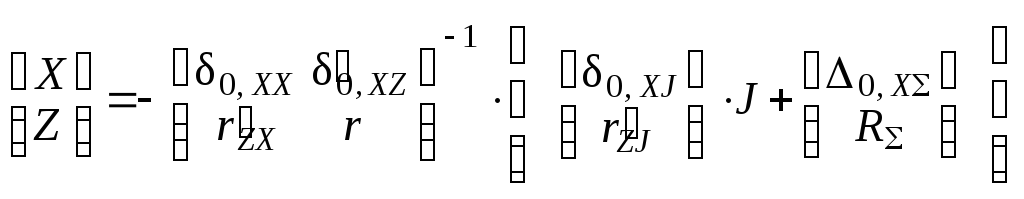( П.12 )

и далее – уравнения ( 1.83 ) для заданной системы, в которых

; ( П.13 )

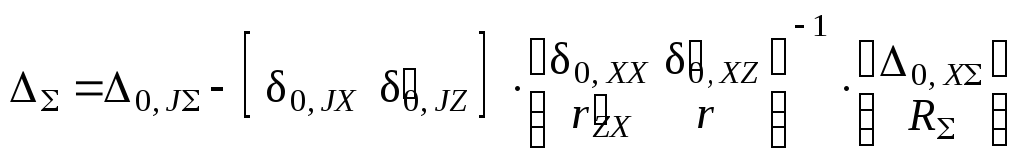. ( П.14 )

Совсем обойтись без вычисления X и Z не удаётся, так как они не-обходимы для определения силовых факторов по ( П.7 ). Поэтому после получения J по ( 1.84 ) используется зависимость ( П.12 ). В случае собственных колебаний в соотношение ( П.10 ) вместо J подставляется

собственный вектор _J(j), в результате чего находится собственный век-

тор неизвестных X и Z: . Компоненты _J(j) , _X(j)и _Z(j) используются в ( П.7 ) вместо J_k , X_k и Z_k при S_{0, } = 0 – таким образом

получаются усилия , необходимые для выполнения кинематичес-кой проверки ( 1.63 ).

Из уравнений и формул ( П.5 ) – ( П.14 ) как частные случаи выво-дятся зависимости, относящиеся к основным системам метода сил и метода перемещений – для этого из вектора Y исключаются некоторые группы неизвестных ( X или Z ), а из матриц коэффициентов и свобод-ных членов – соответствующие блоки. Полученные указанным спосо-бом зависимости сведены в таблицу П.2.

Изложенная выше методика относится к решению задач динамики с помо-щью уравнений, содержащих матрицу податливости системы и силы инерции в качестве основных неизвестных ( см. табл. 1.4 и 1.5 – варианты 2⁰А⁰ и ). В расчётах по уравнениям с матрицей жёсткости естественным и более удобным является использование перемещений в качестве основных неизвестных – главных ( перемещений масс ) и вспомогательных Z, тогда решение в целом вы-полняется методом перемещений – этот подход рассмотрен в п. 1.5.5 ( см. с. 79 ).

Алгоритмы динамических расчётов по уравнениям, записанным для основных систем классических методов, принципиально не отлича-ются от представленных на рис.1.25 и 1.36 – нужно лишь относить все процедуры не к заданной, а к основной системе, вносить поправки в обозначения ( вместо J, – соответственно Y, и т. п .), а также, возможно, вставлять этап преобразования уравнений по со-отношениям ( П.10 ) – ( П.14 ).

Таблица П.2

Тип задачи	Наименования зависимостей	Для основной системы метода сил ( nZ = 0, n0 = n + nX )	Для основной системы метода перемещений ( nX = 0, n0 = n + nZ )
Установившиеся вынужденные колебания при вибрационных воздействиях	Основные уравнения Амплитуды динамических силовых факторов Формулы перехода к уравнениям для заданной системы	Sdyn =++ S0,  ( П.16 ) ( П.17 ) ( П.18 ) ( П.19 )	Sdyn =++ S0,  ( П.26 ) ( П.27 ) ( П.28 ) ( П.29 )
Собственные колебания	Основные уравнения Частотное уравнение Собственный вектор основных неизвестных Формулы пере- хода к уравне- ниям для задан- ной системы	( П.20 ) Det () = 0 ( П.21 ) ( П.22 ) ( П.23 ) ( П.24 )	( П.30 )   Det () = 0 ( П.31 )   ( П.32 ) ( П.33 ) ( П.34 )

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Строительная механика. В 2 кн. Кн. 2. Динамика и устойчи-вость упругих систем : учеб. пособие для вузов / А. В. Александ-ров [и др.] ; под ред. А.В. Александрова. – М. : Высш. шк., 2008. – 384 с.

2. Дарков А. В. Строительная механика : учебник / А. В. Дарков, Н. Н. Шапошников. – 11-е изд., стер.– СПб. : Лань, 2008. – 656 с.

3. Леонтьев Н. Н. Основы строительной механики стержневых систем : учебник / Н. Н. Леонтьев, Д. Н. Соболев, А. А. Амосов. – М. : Изд-во АСВ, 1996. – 541 с.

4. Безухов Н. И., Лужин О. В., Колкунов Н. В. Устойчивость и динамика сооружений в примерах и задачах : учеб. пособие для строит. спец-тей вузов. – 3-е изд., перераб. – М. : Высш. шк., 1987. – 264 с.

5. Себешев В. Г. Строительная механика. Ч. III. Динамика и ус-тойчивость сооружений : иллюстративный конспект лекций [Электронный ресурс] / В. Г. Себешев ; Новосиб. гос. архитек-тур.-строит. ун-т (Сибстрин). – Новосибирск : НГАСУ (Сибст-рин), 2011. – 320 с.

6. Роев В. И. Расчёт статически и динамически нагруженных систем с использованием программного комплекса «DINAM» : учеб. пособие / В. И. Роев ; Новосиб. гос. архитек-тур.-строит. ун-т (Сибстрин). – Новосибирск : НГАСУ (Сибстрин), 2007. – 96 с.

7. Себешев В. Г. Особенности работы статически неопредели-мых систем и регулирование усилий в конструкциях : учеб. пособие / В. Г. Себешев ; Новосиб. гос. архитектур.-строит. ун-т (Сибстрин). – Новосибирск : НГАСУ (Сибстрин), 2009. – 164 с.

8. Феодосьев В. И. Сопротивление материалов : учеб. для вузов. – 10-е изд., перераб. и доп. – М. : Изд-во МГТУ им. Н.Э. Баумана, 2000. – 592 с.

9. Дукарт А. В. Задачи теории ударных гасителей колебаний : монография. – М. : Изд-во АСВ, 2006. – 205 с.

10. Физический энциклопедический словарь / Гл. ред. А.М. Про-хоров. Ред. кол. Д.М. Алексеев, А.М. Бонч-Бруевич, А.С. Боро-вик-Романов и др. – М. : Сов. энциклопедия, 1984. – 944 с.

11. Ишлинский А. Ю. Классическая механика и силы инерции / А. Ю. Ишлинский. – М. : Наука, 1987. – 320 с.

12. Теоретическая механика. Терминология. Буквенные обозна-чения величин : сборник рекомендуемых терминов. – М. : Наука, 1984. – 48 с.

13. Механические колебания. Основные понятия. Терминоло-гия. Буквенные обозначения величин. – М. : Наука, 1987. – 24 с.

14. Казакевич М. И. Аэродинамика мостов / М. И. Казакевич. – М. : Транспорт, 1987, 240 с.

У ч е б н о е и з д а н и е

Себешев Владимир Григорьевич

ДИНАМИКА ДЕФОРМИРУЕМЫХ СИСТЕМ

С КОНЕЧНЫМ ЧИСЛОМ

СТЕПЕНЕЙ СВОБОДЫ МАСС

Учебное пособие

Темплан 2011 г.

Редактор …….

Подписано к печати 00.00.2011 г. Формат 60х84 1/16 д.л.

Гарнитура Таймс. Бумага офсетная. Ризография.

Объем 13,0 уч.-изд.л.; 14,25 п.л. Тираж 200 экз. Заказ №

Новосибирский государственный архитектурно-строительный университет (Сибстрин)

630008, Новосибирск, ул. Ленинградская, 113

rector@sibstrin.ru ; http: //www.sibstrin.ru

Отпечатано мастерской оперативной полиграфии НГАСУ (Сибстрин)

228