4.Задания, приложение, библ

строительной механики

При выполнении динамических расчётов систем с конечным чис-лом степеней свободы масс по уравнениям, записанным для заданной системы, которая, может быть любой – континуальной, пластинчато-оболочечной, стержневой или комбинированной, приходится рассчи-тывать её на действие единичных сил инерции и амплитуд заданных воздействий с определением возникающих от них перемещений или реакций по направлениям степеней свободы масс. В настоящее время это не является проблемой – современные программные средства позволяют с помощью компьютеров рассчитывать конструкции любой сложности эффективными численными методами (методом конечных элементов и др.). Для статически неопределимых стержневых систем сохраняют актуальность классические методы расчёта – сил, переме-щений и смешанный. Их применение в решении задач динамики воз-можно в двух вариантах:

 в качестве вспомогательного средства, играющего сугубо техничес-кую роль в расчёте по уравнениям ( 1.16 ) или ( 1.26) на стадии вычисле-ния компонентов матриц упругой податливости  или жёсткости r за-данной системы и перемещений в ней _P или реакций R_P от амплитуд заданных воздействий;

 с объединением основных неизвестных метода и «главных» неизвест-ных динамического расчёта – сил инерции или перемещений масс – в общий вектор и формированием для его определения уравнений, отно-сящихся уже не к заданной системе, а к основной системе выбранного метода.

Второй вариант не имеет никаких преимуществ в сравнении с пер-вым, а при использовании компьютерных программ даже менее удо-бен. Но, представляя определённый теоретический интерес, он, кроме того, в расчётах «вручную» систем с небольшим числом степеней сво-боды и невысокими степенями статической и кинематической неопре-делимости может быть привлекательным тем, что позволяет заменить n +1 - кратное решение системы канонических уравнений используемого классического метода при расчётах на единичные силы инерции и амп-литуды заданных воздействий (как того требует первый вариант) лишь одним решением общей системы уравнений более высокого порядка (хотя объективно это не дает выигрыша в трудоёмкости).

Рассмотрим решение задачи об установившихся гармонических вынужденных колебаниях консервативной системы с конечным числом степеней свободы 1 n < при вибрационных силовых и кинемати-ческих воздействиях. Исходные предпосылки – те же, что в п. 1.5.5 ( см. с. 70 ). Для раскрытия статической неопределимости заданной системы используем самый общий из классических методов – смешанный.

Как будет показано далее, из полученных уравнений формальным образом затем могут быть выведены уравнения для собственных колебаний, а также для основных систем других методов расчёта статически неопределимых систем.

Применяя кинетостатический метод динамики, считаем систему находящейся в равновесии при амплитудном отклонении от исходного условно недеформированного состояния. В указанном расчётном поло-жении своих амплитудных значений достигают, наряду с силами инер-ции масс и их перемещениями, также и реакции связей, в том числе лишних, и перемещения всех точек системы, включая узлы. За основные неизвестные задачи принимаем амплитуды инерционных силовых фак-торов J, реакций некоторых лишних связей Х и перемещений узлов Z – объединяем их в общий вектор Y = [ J ^т X ^т Z ^т ] ^т. Общее число основных неизвестных n₀ = n + n_X + n_Z , где n_X n_st и n_Z n_к – количества неиз-вестных X и Z соответственно; n_st и n_к – степени статической и кинема-тической неопределимости заданной системы.

Применяя сквозную нумерацию основных неизвестных, имеем

Y = [ J₁ J₂ ... J_n

J₁

y₃

Основная система смешанного метода (ОССМ) получается обыч-ным путем – удалением из заданной системы тех лишних связей, реак-циями которых являются выбранные неизвестные Х (с приложением си-ловых факторов Х взамен удалённых связей), а также наложением на уз-лы, перемещения которых приняты в качестве основных неизвестных Z,

у

J_{n – 1}

гловых и линейных свя-

з

J₃

y_{n – 1}

y₁

ей по направлениям Z,

с

J₂

J_n

заданием этим дополни-

т

F

ельным связям перемеще-

н

y_n

y₂

q

ий, равных Z ( рис. П.1).

J_i

y_k

y_i

Описанный переход

о

y* =__в

J_k

M

т заданной к основной

системе обеспечивает неиз-

м



X_{n + 1}

енность напряжённо-де-

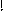
ф

J ^*

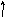
ормированного состоя-

н

X_{n + 2}

ия, следовательно:



Рис. П.1

перемещения масс по

направлениям инерцион-

ных силовых факторов J₁ , J₂ ,..., J_n в основной системе – такие же, как в заданной системе ( истинные ): y_{0, i} = y_i , i = 1, 2, ..., n; ( П.1 )



Здесь и далее нижний индекс «0» в обозначениях переме-щений y_{0, i} и _{0, i} указывает на то, что они определяются в основной системе.

перемещения в основной системе по направ-

лениям удаленных абсолютно жёстких лиш-

них связей равны нулю:

_{0, i} = 0, i = n + 1, n + 2, ..., n + n_X ; ( П.2 )

 реакции дополнительных связей, наложенных на узлы, равны нулю:

R_i = 0, i = n + n_X + 1, n + n_X + 2, ..., n₀ . ( П.3 )

Уравнения ( П.1 ) – ( П.3 ) выражают условия эквивалентности НДС двух систем – основной смешанного метода и заданной. Представляя их левые части по принципу суперпозиции как суммы составляющих от основных неизвестных J, X, Z и амплитуд заданных воздействий, согласно рис. П.1, получаем:

y

i =1, ..., n ;

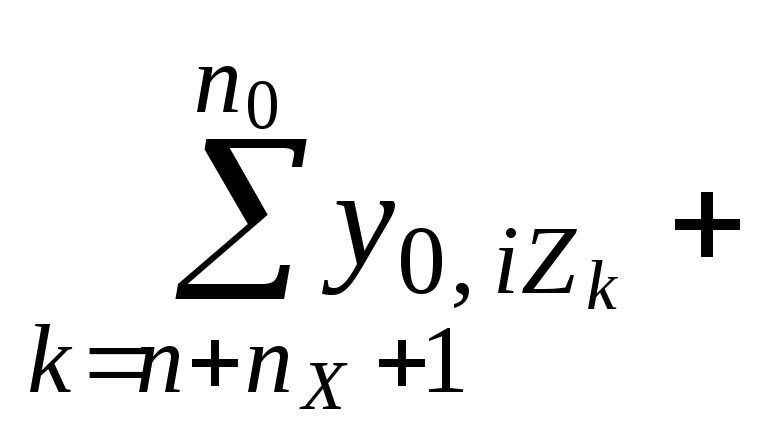_{0, iJ} + y_{0, iX} + y_{0, iZ} + _{0, i}= _{0, i}= y_i ,



i = n + 1, ..., n + n_X ;

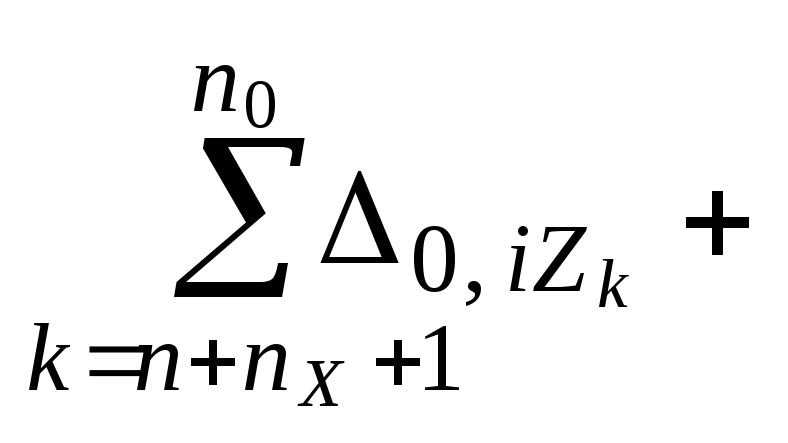_{0, iJ} + _{0, iX} + _{0, iZ} + _{0, i}=_{0, i}= 0 ,



i = n + n_X + 1, ..., n₀

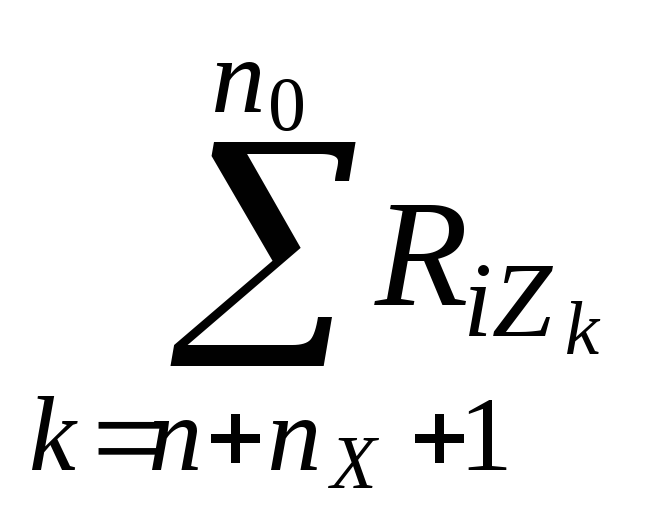R_iJ + R_iX + R_iZ + R_i =+++ R_i= 0,

или, заменяя величины, стоящие под знаками сумм, произведениями единичных перемещений и реакций на соответствующие неизвестные J_k , X_k и Z_k :

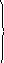
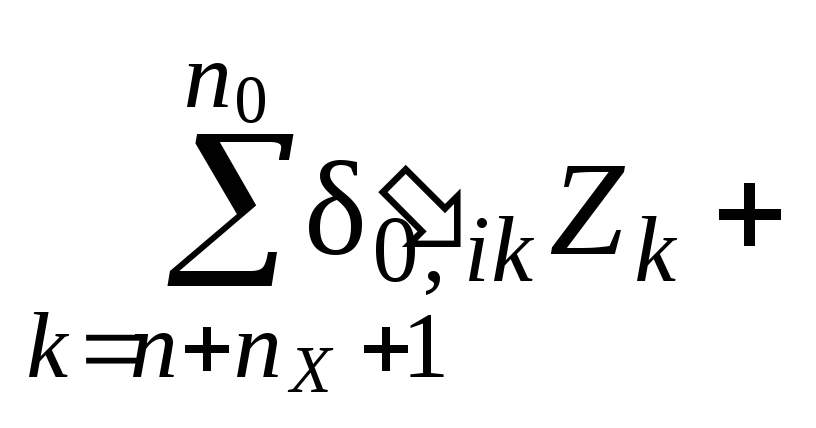_{0, i} = y_i , i = 1, ..., n ;

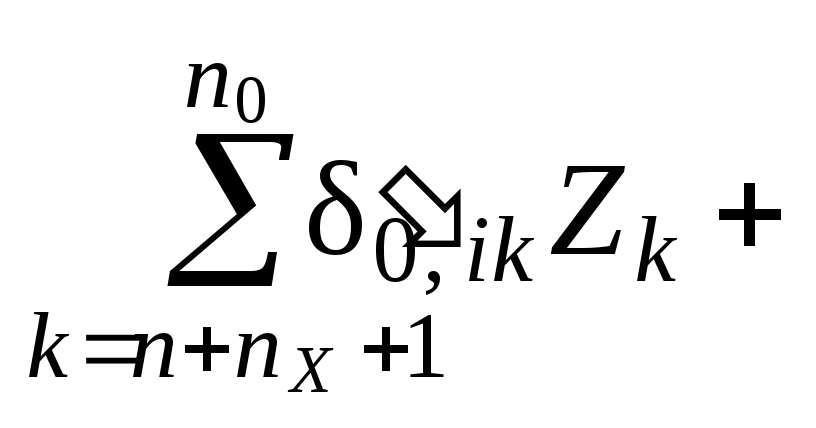_{0, i} = 0, i = n +1, ..., n + n_X ; ( П.4)

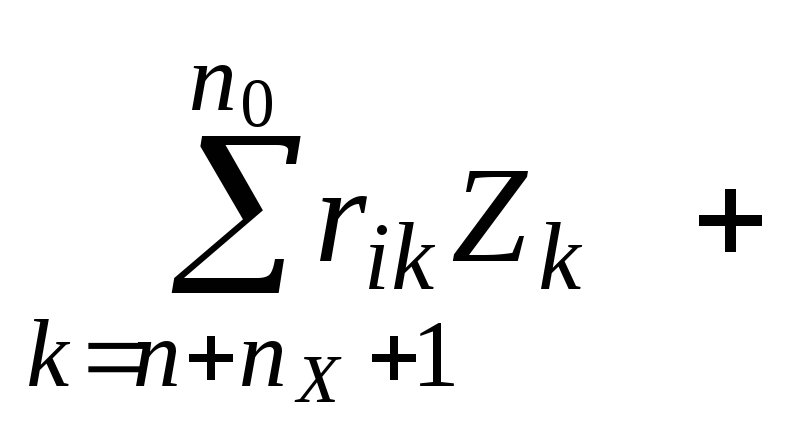R_i = 0, i = n + n_X + 1, ..., n₀.

Выразив y_i ( i = 1, 2, ..., n ) через J_i по ( 1.81 ), получим основные уравнения установившихся вынужденных колебаний, записанные для основной системы смешанного метода в канонической форме:

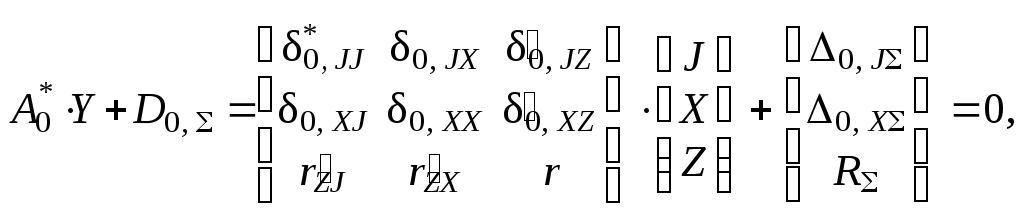( П.5 )

г

. . . . . . . . . . . . . . . .

= _{0, ii} – 1/() = _{0, ii} – _F /a _i .

де = _{0, JJ} – _F a ^–1 = _{0, JJ} – ( m₀) ^–1 a ^–1 =;

Смысл блоков матрицы коэффициентов и вектора свободных членов D_{0, } уравнений ( П.5 ) расшифровывает следующая таблица:

Сущность величин, являющихся компонентами блока	От каких воздействий возникают величины, являющиеся компонентами блока От единичных От единичных От единичных От амплитуд сил инерции реакций лишних перемещений заданных Jk = 1, связей Xk=1, узлов Zk = 1, воздействий k = 1, ..., n k = n+1, ... , k = n+nx+1, n+nx ..., no
По направлени- ям сил инерции Пере- J1 , J2 , ..., Jn меще- По направлени- ния в ям удаленных ОССМ лишних связей или их реакций Xn+1, Xn+2 , ..., Xn+nX Реакции связей, введённых в узлы ОССМ	0, J 0, X r R

Блоки матрицы подчиняются условиям взаимности:;

 а внутри диагональных блоков _{0, JJ} , _{0, XX} и r : _{0, ik} = _{0, ki} ; r_ik = r_ki ( ik ).

Структура и размеры блоков таковы:

_nn )

_nn_X )

. . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . .

; ;

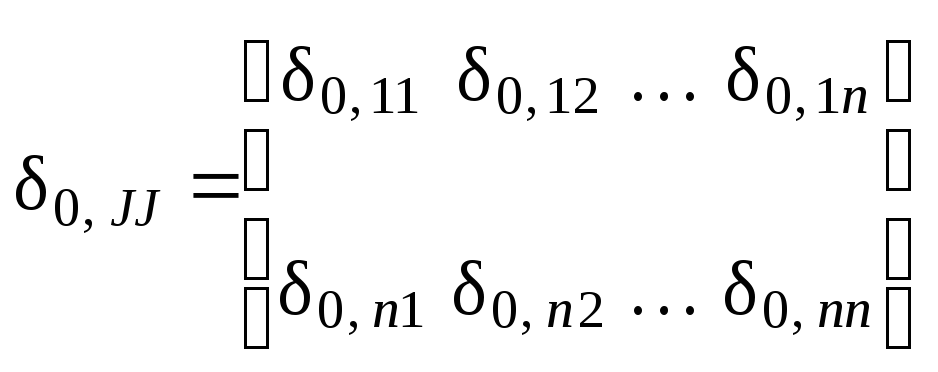
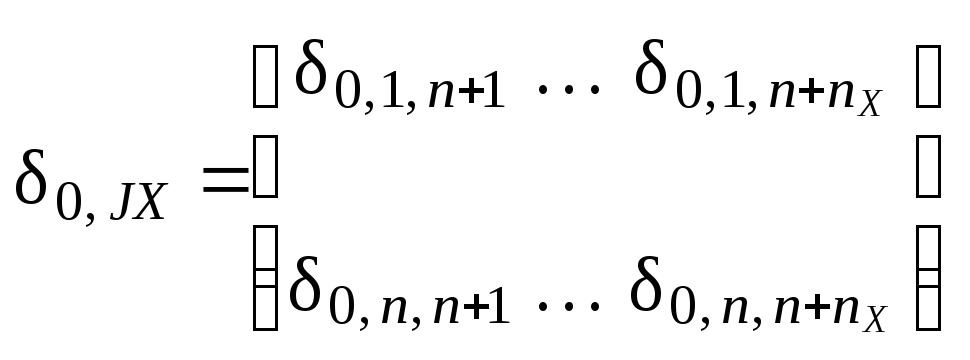_nn_Z )

_n_X  n )

. . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . .

; ;

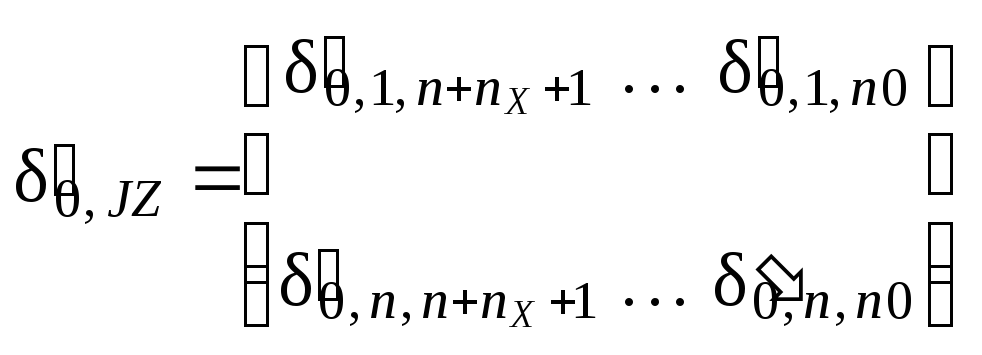
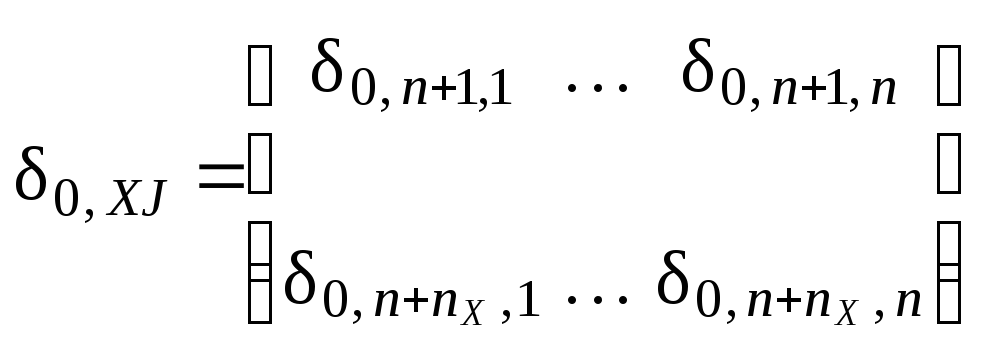_n_X  n_X )

_n_X  n_Z )

. . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . .

; ;

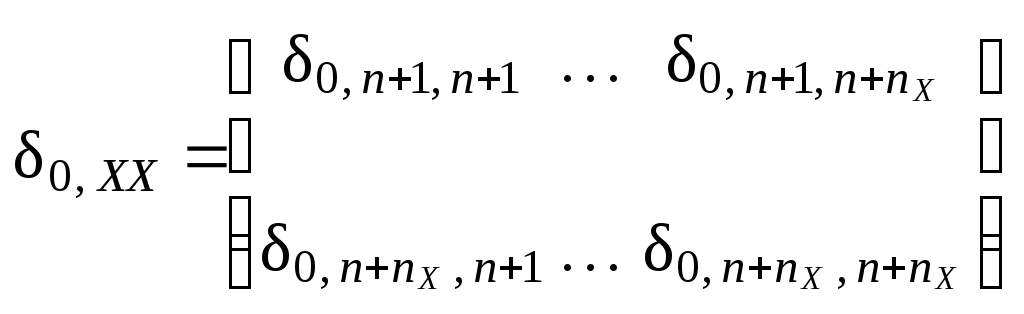
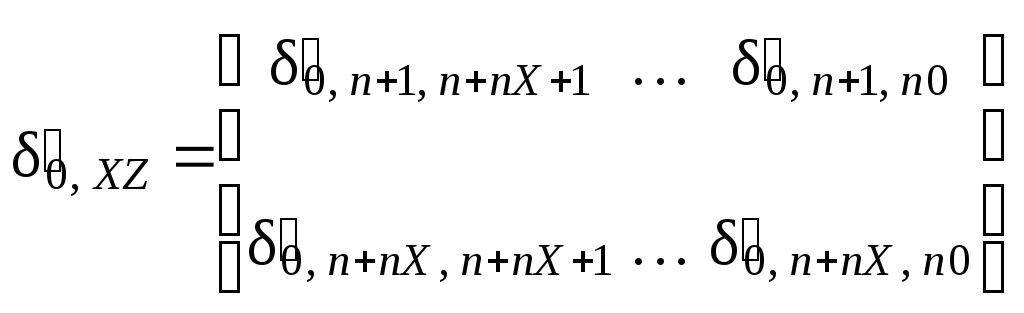_n_Z  n )

_n_Z  n_X )

. . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . .

; ;

. . . . . . . . . . . . . . . . . . . .

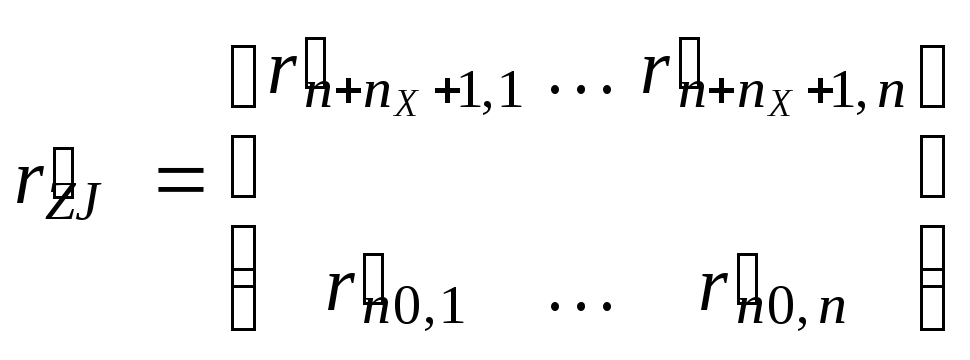_n_Z  n_Z )

_n  1 )

_n_X  1 )

;

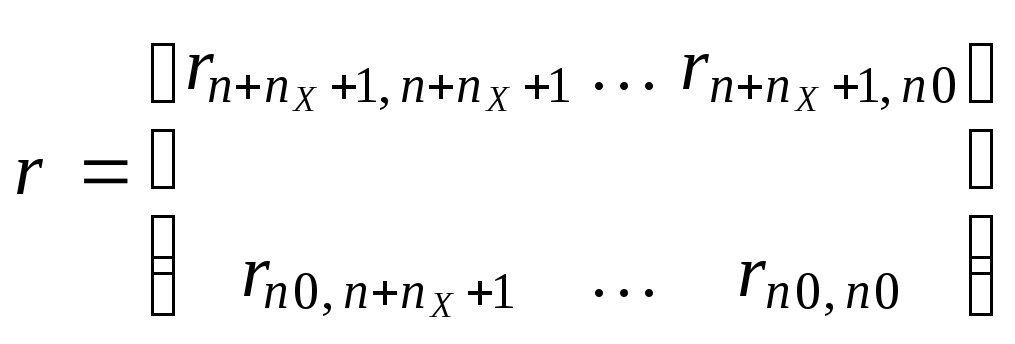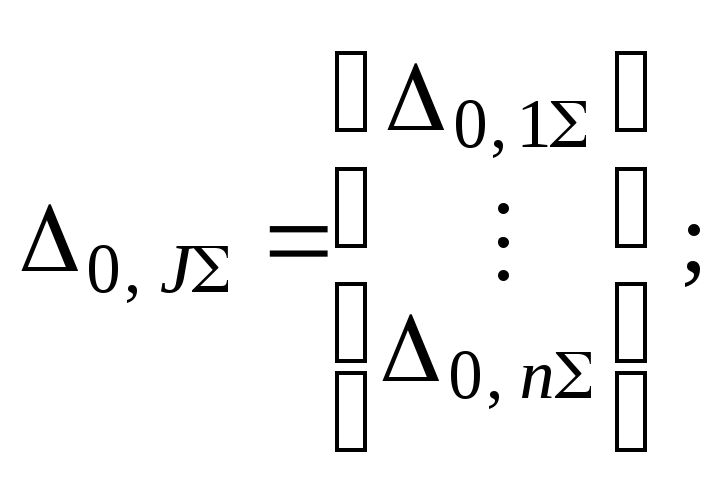
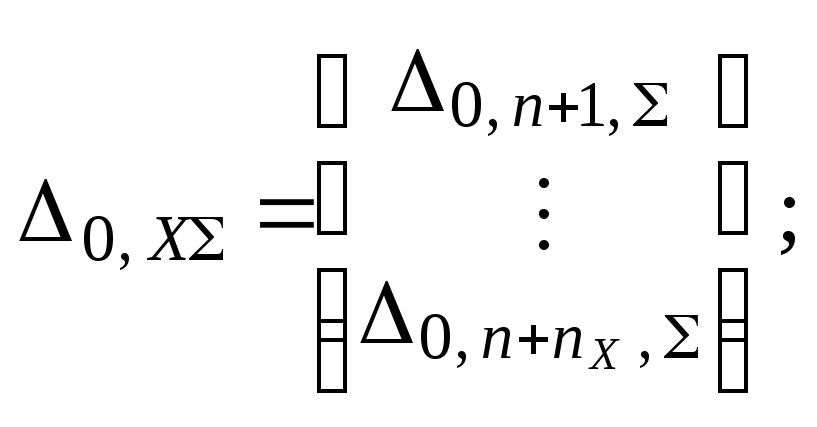
_n_Z  1 )

_{} Следует обратить внимание на то, что динами-

ческие поправки, содержащие , входят толь-

ко в n диагональных членов блока .

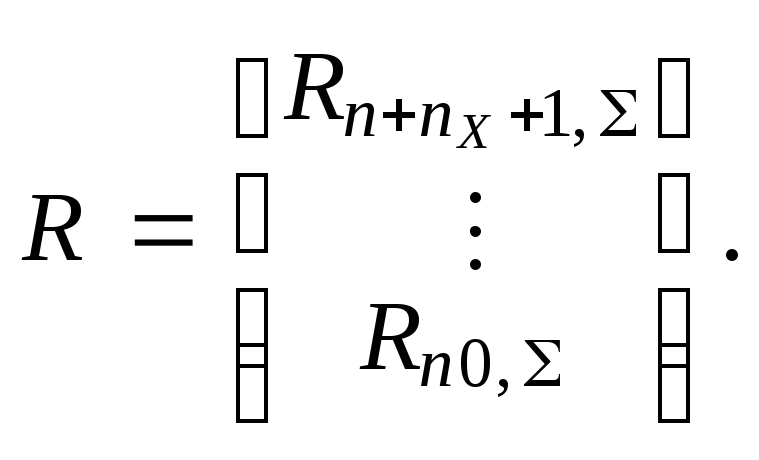
Компоненты блоков _{0, JJ} , , _{0, XX} , _{0, J} и _{0, X} опреде-

ляются как перемещения – методом Максвелла – Мора или любыми дру-

гими методами, пригодными для рассматриваемой системы. Единич-

ные реакции – компоненты блоков, – и R_i из R_ могут вычис-

ляться статическим и кинематическим способами, а r_ik в блоке r – также

и «перемножением» единичных эпюр. Величины в блоках и

находятся из условия взаимности . Для вычисления на-

званных компонентов матриц предварительно определяются в основ-ной системе силовые факторы S_{0, k} ( k = 1, 2, ..., n₀ ) от единичных оcнов-ных неизвестных и S_{0, } – от амплитуд воздействий.

 ( П.6 )

Решением системы уравнений ( П.5 ) отыскиваются основные не-известные задачи

Очевидно, что должно быть Det. Матрица может оказаться вырожденной ( Det) либо при _F = _(случай резонанса), либо при вы-

боре основной системы, не являющейся геометрически неизменяемой – в обоих

случаях должны быть внесены необходимые исправления.

По найденным J, X и Z далее вычисляются искомые амплитуды динамических силовых факторов:

S_dyn =+++ S_{0, }( П.7 )

после чего выполняются статическая и кинематическая проверки ре-зультатов расчёта ( напомним, что в смешанном методе обе они одина-ково важны ), причем в кинематической проверке контролируются и амплитуды динамических перемещений масс ( как в п. 1.5.5 – по ( 1.87 )), и перемещения по направлениям удаленных лишних связей в ОССМ

( вычисленные по правой части формулы ( 1.87 ) с S_i и R_j,i от X_i = 1, они

должны быть равными нулю ).

Всё остальное – построение эпюр динамических усилий, опреде-ление расчётных усилий и т.д. – осуществляется так же, как в расчёте по уравнениям, относящимся к заданной системе ( п. 1.5.5 ).

Основные уравнения для задачи о собственных колебаниях, за-писанные для основной системы смешанного метода, легко получают-ся с помощью уравнений ( П.5 ) из следующих соображений: собствен-ные колебания происходят по гармоническому закону, как и рассмот-ренные выше установившиеся вынужденные, но с частотой , а не _F . Поэтому, если на схеме ( рис. П.1 ) считать отсутствующими заданные нагрузки F, q, M и смещения связей , то полученная расчётная схема ОССМ будет относиться к случаю собственных колебаний. Она описы-вается уравнениями, формально вытекающими из ( П.5 ), если принять

_{0, } = 0 и заменить на , на :

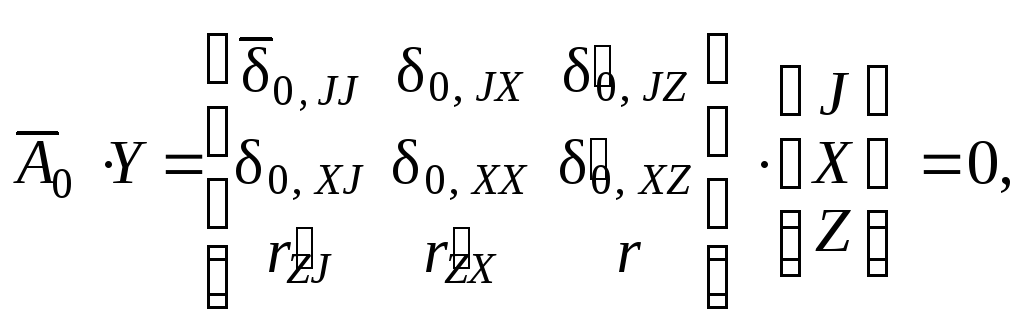( П.8 )

г

. . . . . . . . . . . . . . . .

= _{0, ii} – 1/() = _{0, ii} –  /a _i .

де = _{0, JJ} –  a ^–1 = _{0, JJ} – ( m₀) ^–1 a ^–1 =;

Det () = 0 . ( П.9 )

Частотное уравнение получается из условия существования коле-баний Y 0: