2. Схемы включения корректирующих устройств

Рассмотрим наиболее распространённые структурные схемы включения корректирующих устройств [9-14, 21-25]. При последовательной коррекции (рис. 9) регулятор включается последовательно с объектом управления

Рис. 9

(системы с последовательной коррекцией). Передаточная функция разомкнутой системы

Wraz (s) = Wp(s) Wo (s);

 передаточная функция замкнутой системы

.

При встречно-параллельной коррекции корректирующее устройство включается в цепь обратной связи (рис. 10).

Рис. 10

Передаточная функция замкнутой системы

.

Передаточные функции систем имеют одно и тоже характеристическое уравнение

,

следовательно, их динамические свойства одинаковы. Однако в предельном случае (k→∞) систему с последовательной коррекцией можно рассматривать как пропорциональное звено (Wzam (s)=1), а свойства системы с встречно-

параллельной коррекцией не зависят от характеристик объекта (Wzam(s)=1/Wp(s)) и определяются характеристикой регулятора.

На рис. 11 представлена схема комбинированной коррекции, которая дает наилучший результат при изменении как задания, так и нагрузки.

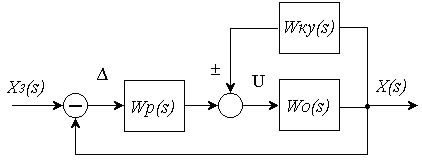
Рис. 11

Существуют и другие способы включения корректирующих устройств.

3. Типовые алгоритмы управления и типовые регуляторы

В качестве корректирующих устройств чаще всего применяются аналоговые и дискретные регуляторы следующих типов:

- пропорциональные (П) – реализуются при помощи усилителей (рис. 12)

Рис. 12

с передаточной функцией

Wp(s) = k_Р =k_П;

управляющее воздействие таких регуляторов и в статике и в динамике пропорционально сигналу ошибки, они обладают высоким быстродействием и ограниченной точностью при управлении инерционными объектами; статическая ошибка обратно пропорциональна коэффициенту передачи; на рис. 13 представлена переходная характеристика регулятора (k_П = 2), на рис. 14 - логарифмические амплитудная и фазовая характеристики (диаграмма Боде);

Рис. 13

Рис. 14

- интегральные (И) – реализуются с помощью звена (рис. 15)

Рис. 15

с передаточной функцией

Wp(s) = k_I / s = k_P /Т_I s;

управляющее воздействие в каждый момент времени пропорционально интегралу от сигнала ошибки, обладает высокой точностью в установившемся режиме (при t → 0 k_I → ∞), меньшим быстродействием и большей колебательностью; скорость перемещения вала исполнительного механизма (ИМ) пропорциональна величине отклонения регулируемого параметра от заданного; динамический параметр настройки регулятора k_P численно равен величине скорости перемещения вала ИМ, приходящейся на единицу отклонения регулируемого параметра от заданного; постоянная Т_I количественно характеризует скорость изменения выходной величины, приходящейся на единицу изменения входной величины, чем больше Т_I, тем меньше изменение выходной величины в единицу времени; эту постоянную называют время удвоения или время изодрома; на рис. 16 и 17 показаны динамические характеристики такого регулятора при k_P = 2 и T_I = 0,5 c.

Рис. 16

Рис. 17

- пропорционально – интегральный (ПИ) – реализуется звеном (рис. 18)

Рис. 18

с передаточной функцией

W_p(s) = k_п + k_I /s = k_Р + k_Р /T_I s = k_P (T_I s + 1)/Т_I s;

обладает достоинствами и недостатками первых двух; время изодрома Т_I – это время, за которое угол поворота вала ИМ под действием пропорциональной части удваивается интегральной частью, поэтому Тi называют временем удвоения; динамические характеристики регулятора представлены на рис. 19 и 20;

Рис. 19

Рис. 20

- пропорционально–дифференциальный (ПД) – реализуется звеном (рис. 21) с передаточной функцией

W_p(p) = k_П + k_d s = k_P + k_P Т_d s;

Рис. 21

регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения, благодаря этому достигается эффект упреждения; за время предварения Т_d угол поворота вала ИМ под действием дифференцирующей части удваивается (это время, за которое входная величина, изменяясь с постоянной скоростью, достигает значения выходной величины). На рис. 22 представлена ЛФЧХ такого регулятора при k_P = 2 и T_d =0,5 c. Переходной процесс при единичном входном ступенчатом воздействии содержит дельта-функцию.

Рис. 22

Промышленные регуляторы реализуют операцию дифференцирования с помощью реального дифференцирующего звена (рис. 23), передаточная функция которого

, N – const, N = 3 - 10.

Рис. 23

На рис. 24 и 25 представлены динамические характеристики такого регулятора при k_P = 2, T_d = 0.5 и N = 10.

Рис. 24

Рис. 25

- пропорционально-интегрально-дифференциальный (ПИД) – реализуется звеном (рис. 20) с передаточной функцией

W_p(s) = k_П + k_I /s + k_d s = k_P(1 + Т_I s + T_IT_d s²)/Т_I s =

и обеспечивает наилучшие показатели качества переходных процессов; регу-

лятор может быть представлен как последовательное или параллельное соединение звеньев (рис. 26).

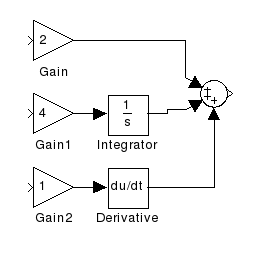
Рис. 26

Промышленный регулятор (рис. 27) имеет передаточную функцию

где N – обычно фиксируется проектировщиком в диапазоне 3 – 10. Его динамические характеристики представлены на рис. 28 и 29.

Рис. 27

Рис. 28

Рис. 29

Классические ПИ – и ПИД – регуляторы имеют различные структуры (рис. 30), которые могут быть использованы как в непрерывном, так и в дискретном случае. Структуры идеального и реального регуляторов представлены на рис. 30а, б и г.

Структуру ПИ – регулятора можно рассматривать как последовательное соединение форсирующего и интегрирующего звеньев. Такой регулятор обладает свойством упреждения: выходной сигнал сдвинут так, как будто интегрирование началось раньше входного сигнала на время изодрома. Последовательное соединение П – и И – регуляторов составляет структуру И – регулятора, но изменяет время интегрирования в k_Р раз. Параллельное соединение этих же регуляторов дает структуру ПИ – регулятора. Последовательное соединение ПД – и И – регуляторов порождает ПИ – регулятор, параллельное соединение этих же регуляторов порождает ПИД – регулятор. Последовательное и параллельное соединение ПИ – ПД – регуляторов порождает структуру ПИД – регуляторов, но с разными параметрами.

Регулятор структуры рис. 30г не даёт большого управляющего сигнала при скачкообразном изменении задающего воздействия.

Структура 30д даёт наилучший результат как при изменении задания, так и при изменении нагрузки (разница в параметрах регулятора минимальна, если он настроен по входному сигналу или по возмущениям процесса).

Регулятор с фильтром, передаточная функция которого

,

позволяет фильтровать все три части регулятора или только пропорциональную и дифференциальную части. В этом случае можно уменьшить высокочастотный шум измерений.

Рис. 30

Если фильтр нижних частот соединить последовательно с ПИ – регулятором (рис. 30е) или два ПИ – регулятора соединить каскадно, то получится структура, известная под названием ПИ² – регулятор (PIPI controller). Такие регуляторы иногда используются в системах электропривода. Фильтр нижних частот ослабляет уровень высокочастотных сигналов и хорошо гасит резонансные колебания в системах механического привода. Передаточная функция регулятора

Значение Т_Ф1 обычно принимается равным резонансному периоду. ЛАЧХ регулятора представлена на рис. 31.

Рис. 31

Типовые регуляторы являются идеальными динамическими звеньями. Свойства реальных регуляторов могут значительно отличаться от идеальных и допустимые отклонения регламентированы стандартом на промышленные регуляторы.

Работа регуляторов и системы в целом оценивается показателями качества.