§ 5.4. Проверка адекватности регрессионной модели

На этом этапе оценивается пригодность регрессионной модели для решения задач анализа и прогноза исследуемых экономических процессов.

Традиционными методами анализа адекватности линейной регрессионной модели (ЛРМ) являются:

1) дисперсионный анализ модели,

2) анализ остатков (отклонений, возмущений),

3) статистическая проверка гипотез о параметрах модели и уравнении в целом.

Дисперсионный анализ (ANOVA) ЛРМ заключается в оценивании вклада в дисперсию зависимой переменной Y, которую вносят включенные в модель независимые переменные и неконтролируемые случайные факторы, приводящие к случайным ошибкам наблюдения .

Основное уравнение дисперсионного анализа имеет вид:

где – сумма квадратов отклонений зависимой переменной от выборочного среднего значения

,

называемая полной суммой квадратов;

–

сумма квадратов отклонений прогнозных значений от среднего, обусловленная регрессионной моделью, т.е. включенными в модель переменными;

–

сумма квадратов остатков (или остаточная сумма квадратов).

Всякая сумма квадратов связана с числом, называемым ее степенями свободы, т.е. числом независимых элементов информации, получающихся из n независимых величин . Число степеней свободы для перечисленных сумм квадратов простой линейной регрессии соответственно равно:

.

Они удовлетворяют уравнению: .

Для множественной линейной регрессии

.

Важной характеристикой адекватности ЛРМ является величина

,

называемая коэффициентом детерминации модели (см. множественный коэффициент корреляции ).

Характеристикой точности прогноза на основе построенной модели является среднеквадратическая (стандартная) ошибка прогноза, совпадающая с оценкой среднеквадратического (стандартного) отклонения ошибок:

.

§ 5.5. Анализ остатков

В предыдущем рассмотрении простой линейной регрессии были сделаны три предположения. Они касались формы модели, распределения и случайности величины ошибки . Все три предположения могут быть проверены при рассмотрении графиков остатков . Такие графики включены в состав выходных данных программ большинства ПСП.

Для проверки адекватности модели можно использовать график d_i в зависимости от x_i или . Если остатки попадают в горизонтальную полосу с центром на оси абсцисс, модель можно рассматривать как адекватную (рис. 5.3, а). Если полоса расширяется, когда х или возрастает (рис. 5.3, b), это указывает на гетероскедастичность (т.е. на отсутствие постоянства дисперсии ²). В частности,  может быть функцией , что делает необходимым преобразование переменной Y. График, показывающий линейный тренд (рис. 5.4.), дает основание для введения в модель дополнительной независимой переменной (см. § 5.3). График вида, представленного на рис. 5.3. d, указывает, что в модель должен быть добавлен линейный или квадратичный член.

Для проверки нормальности , подходит гистограмма d_i. Нормальность может быть также проверена с помощью критериев согласия.

Р ис. 5.3. Примеры графиков остатков. А – адекватная модель;

b – гетероскедастичность; с – линейная независимая переменная;

d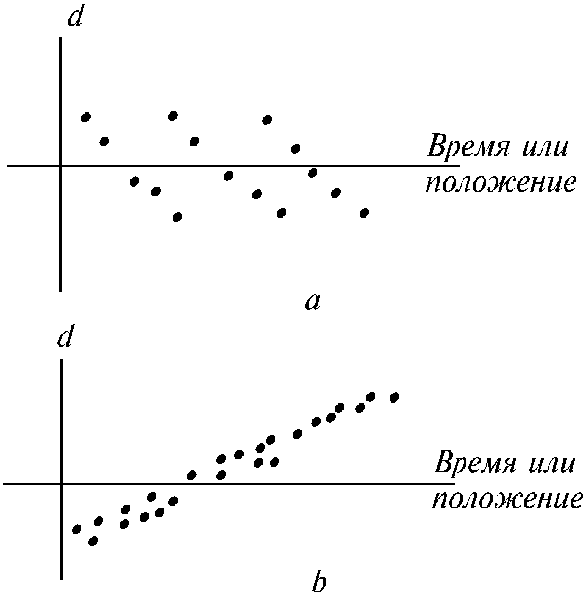 – линейная или квадратичная независимая переменная.

Рис. 5.4. Примеры отсутствия случайности.

а – сезонный тренд; b – линейный тренд.