5.2. Проверка гипотез и доверительные интервалы

Чтобы сделать статистические выводы об а₀, а₁ и , сначала необходимо оценить дисперсию ², а затем описать распределение ошибки случайной переменной . Согласно теории общей линейной модели, обычная несмещенная оценка для ² определяется через дисперсию оценки

.

Положительный корень из этой величины называют стандартной ошибкой оценки. Если ошибки предполагаются нормальными, т.е. распределенными по закону , и независимыми, то можно проверить гипотезы о параметрах и построить для них доверительные интервалы. Для проверки гипотезы , где – некоторая константа, например , используем статистику

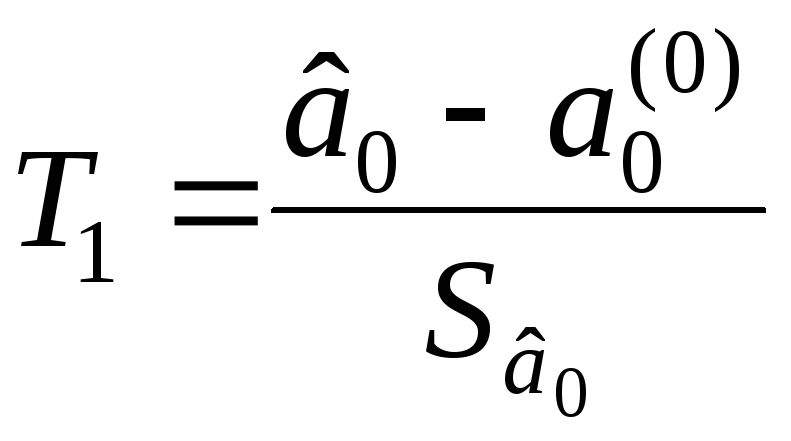, где .

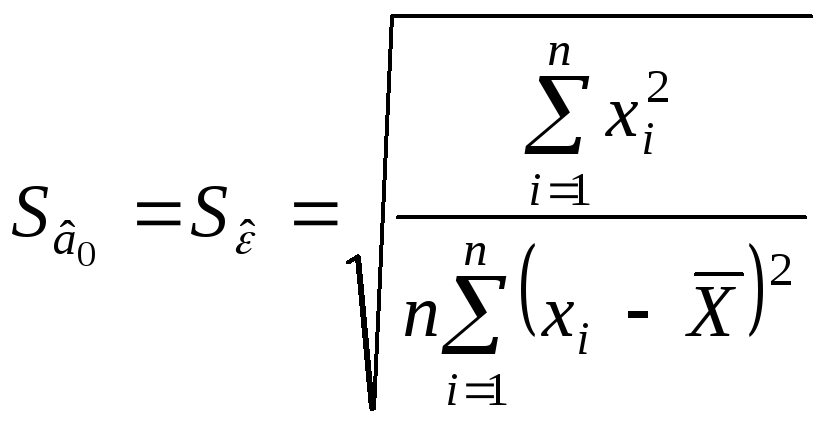Для проверки гипотезы , где – некоторая константа, используем статистику

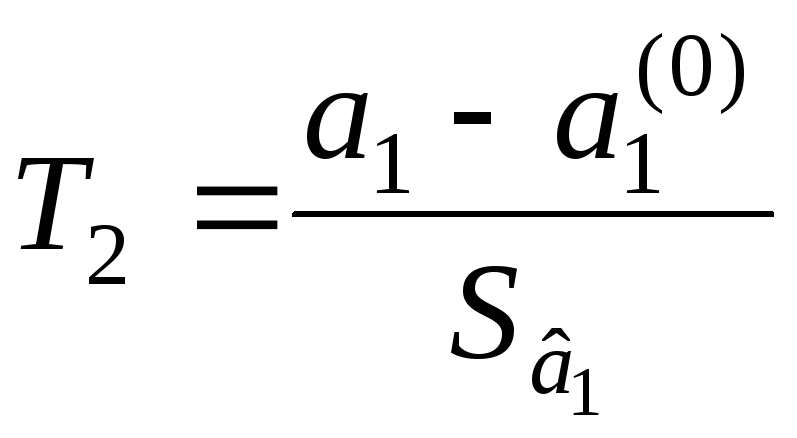, где .

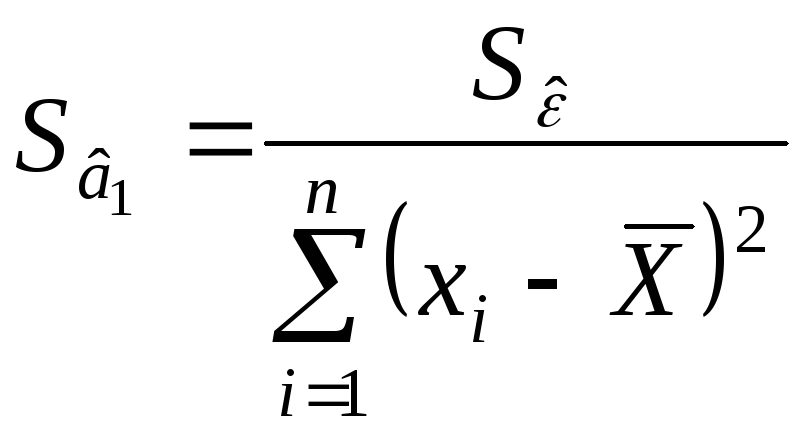Если гипотеза Н₀ верна, то Т₁ и Т₂ имеют распределение Стьюдента с n – 2 степенями свободы.

Если гипотеза Н₀ принимается для а₀, то прямая проходит через начало координат.

Если гипотеза Н₀ принимается для а₁, то этот параметр незначим, т.е. отсутствует влияние х на зависимую переменную и математической модели зависимости Y от Х не существует.

Если гипотеза Н₀ отвергается, то параметр а₁ интерпретируется следующим образом: если независимая переменная Х изменится на одну единицу своего измерения, то (при прочих равных условиях) зависимая переменная изменится в среднем на единиц своего измерения (смотри далее эластичность).

Для проверки гипотезы о том, что простая линейная регрессия Y по Х отсутствует, т.е. гипотез мы воспользуемся F-отношением из таблицы дисперсионного анализа (табл. 5.1).

Таблица 5.1. Анализ дисперсий.

(Формулы для вычисления SS_D,

SS_R, SS_T, n_D, n_R приведены в § 5.4.)

Источник вариации	Суммы квадратов	Степени свободы	Средние квадраты	F-отношение (Тнабл)	Уровень значимости
Модель	SSD	nD	MSD = SSD / nD	F = MSD/ MSR	 набл.
Ошибка	SSR	nR	MSR = SSR/ nR
Итого (скорр.)	SST	nT = n – 1

Принятие Н₀ означает, что модель в целом не адекватна, так как фактор Х, включенный в модель, не оказывает влияния на зависимую переменную Y и может быть исключен из модели. Принятие Н₁ означает, что Х оказывает значимое влияние на зависимую переменную Y.

Доверительные интервалы для а₀ и а₁ с доверительной вероятностью  вычисляются по формулам:

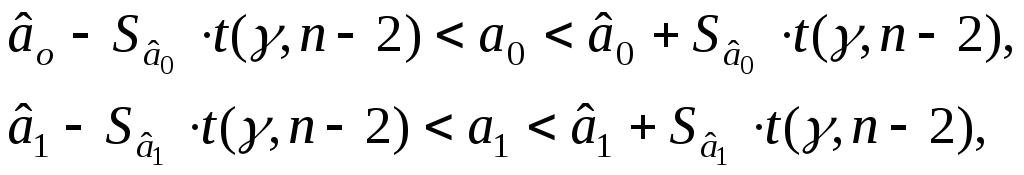
где – квантиль уровня  распределения Стьюдента с k = n – 2 степенями свободы, – среднеквадратические (стандартные) ошибки оценок а₀ и а₁ соответственно.

Доверительные интервалы для прямой регрессии.

Каждая заданная прямая регрессии при изменении смещается параллельно самой себе вверх или вниз. Если изменяется а₁, то прямая поворачивается вокруг точки .

Определим две стандартные ошибки:

1. для среднего значения в точке х:

,

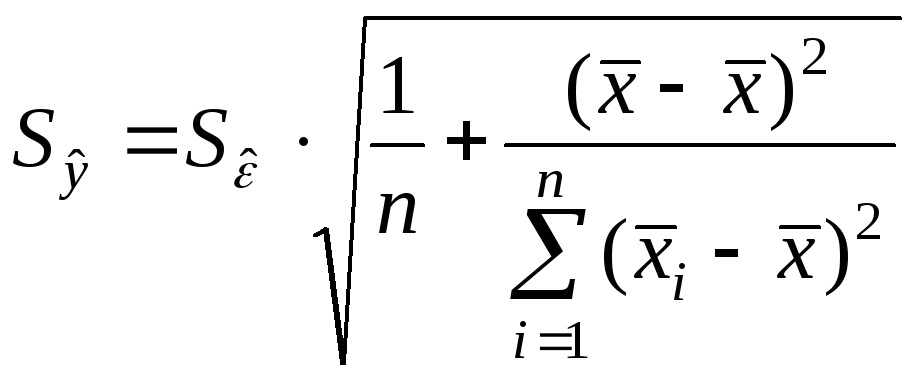2. для индивидуального значения в точке х:

.

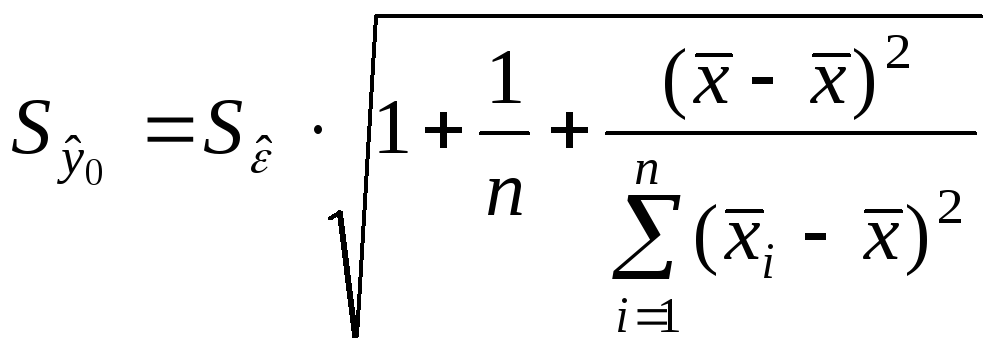Тогда доверительные интервалы для

1) всей прямой регрессии:

;

где – квантиль уровня  F-распределения с n₁ = 2 и n₂ = n – 2 степенями свободы;

2) среднего значения наблюдения в точке х:

;

3) индивидуального наблюдения в точке х:

.

Эти интервалы справедливы только для области измерений (наблюдений). При удалении от точки статистическая ненадежность оценок возрастает. Наибольший доверительный интервал – для (1), наименьший – для (2).

Пример. В теме «Корреляционный анализ» рассматривается зависимость веса женщин (Y) от роста (Х). Выборочный коэффициент корреляции r_XY = 0,9, следовательно, существует линейная зависимость между ростом женщины и ее весом:

.

Определим оценки неизвестных параметров а₀ и а₁, а также дисперсию отклонений . Обратившись к методу наименьших квадратов, получим систему уравнений:

решив которую, получим: . Запишем уравнение простой регрессии:

.

Проверим на уровне значимости  = 0, 05 гипотезу против альтернативы . Вычислим , где .

Находим по таблице t-распределения значение .

Так как , то гипотеза Н₀ отвергается. Интерпретация : если рост женщины увеличится на 1 см, то при прочих равных условиях ее вес в среднем увеличится на 0,8113 кг.