120

Тема 5. Регрессионный анализ § 5.1. Простая линейная регрессионная модель и оценивание по методу наименьших квадратов

В регрессионном анализе рассматривается связь между одной переменной, называемой зависимой переменной, и несколькими другими, называемыми независимыми переменными. Эта связь представляется с помощью математической модели, т.е. уравнения, которое связывает зависимую переменную с независимыми с учетом множества соответствующих предположений. Независимые переменные связаны с зависимой посредством функции регрессии, зависящей также от набора независимых параметров. Если функция линейна относительно параметров (но не обязательно линейна относительно неизвестных переменных), то говорят о линейной модели регрессии. В противном случае модель называется нелинейной. Выбор подходящей модели основывается на экономической (или другой) теории и не является статистической задачей.

Рассмотрим два типа линейных по параметрам регрессионных моделей – простую и множественную.

Простая регрессия

Для простоты рассмотрим зависимость Y от одной переменной Х.

Определение. Уравнением регрессии Y на Х называется условное математическое ожидание Y при фиксированном значении Х = х, т.е. . Аналогично определяется и уравнение регрессии Х на Y, т.е. .

Функции f(x) (или (y)) являются математическими моделями зависимости. Однако не существует теории, позволяющей по наблюдаемым данным определить конкретный вид модели. Эту задачу специалист решает, исходя из знаний в своей предметной области. Большую помощь в определении математической модели оказывает анализ диаграммы рассеяния (см. Корреляционный анализ).

Если предполагается линейная зависимость между Y и Х, то теоретическая модель задается уравнениями

и называется моделью простой линейной регрессии. Величины а₀ и а₁ являются неизвестными параметрами, а суть некоррелированные ошибки случайной переменной со средним, равным нулю, и неизвестной дисперсией , т.е.

и .

Н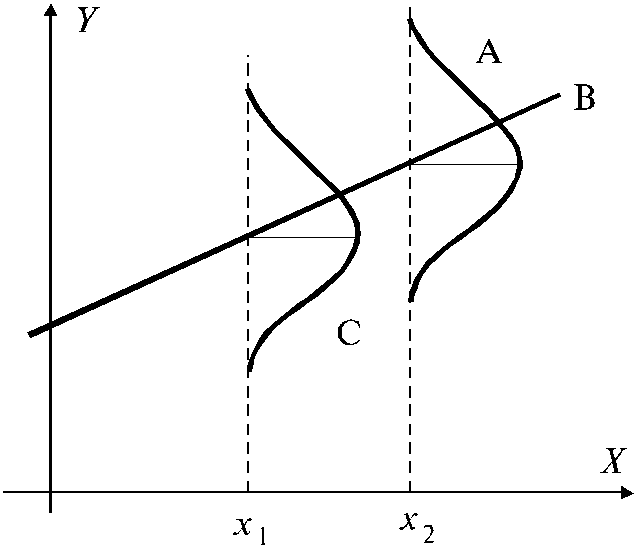 а рис. 5.1. эта модель представлена графически

Рис. 5.1. Модель простой линейной регрессии. В – прямая ,

А – распределение Y для Х = х₁, среднее , дисперсия ²;

С – распределение Y для Х = х₂, среднее , дисперсия ².

Для каждого значения X = x_i имеется распределение (не обязательно нормальное!) со средним значением и дисперсией .

Найдем теперь оценку неизвестных значений a₀ и a₁, основанную на выборке объема n. Наилучшие оценки и для a₀ и a₁ получаются минимизацией соответственно по a₀ и a₁ сумм квадратов отклонений

.

Необходимые условия минимума S:

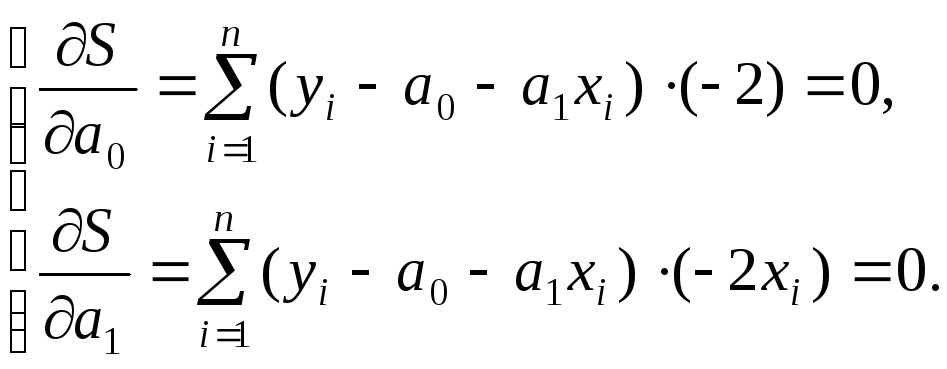
Выполнив необходимые вычисления, получим систему двух линейных уравнений с двумя неизвестными a₀ и a₁

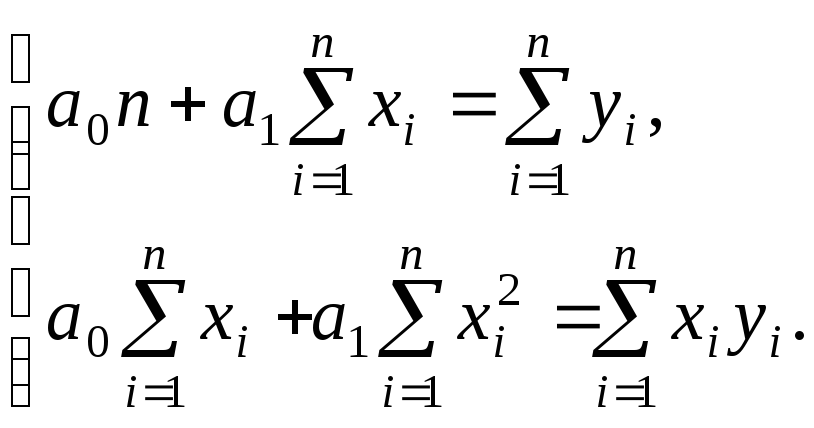
Разделив каждое уравнение на n, получим

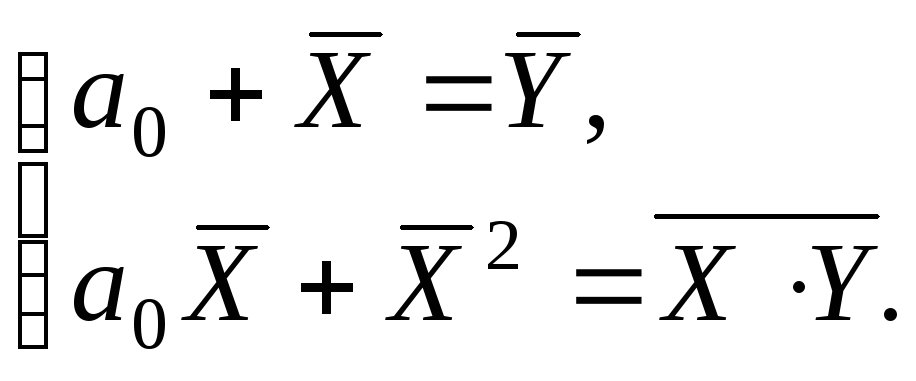
Решение системы: . Полученные оценки называются оценками наименьших квадратов. Если известен коэффициент корреляции r_xy, то

.

Заметим, что S есть мера ошибки, возникающей при аппроксимации выборки прямой. Оценки и минимизируют ошибку. Они являются несмещенными и имеют минимальную дисперсию среди всех несмещенных оценок а₀ и а₁, линейно зависящих от наблюдений .

Оценкой уравнения регрессии (или прямой наименьших квадратов) будет

так что оценка значения Y при X = x_i есть .

Разница между наблюденным и оцененным значением Y при X = x_i называется отклонением (или остатком) .

Прямая наименьших квадратов доставляет минимум сумме квадратов отклонений

.

Соотношение между теоретической регрессионной прямой, прямой наименьших квадратов и точками выборки можно увидеть на рис. 5.2.

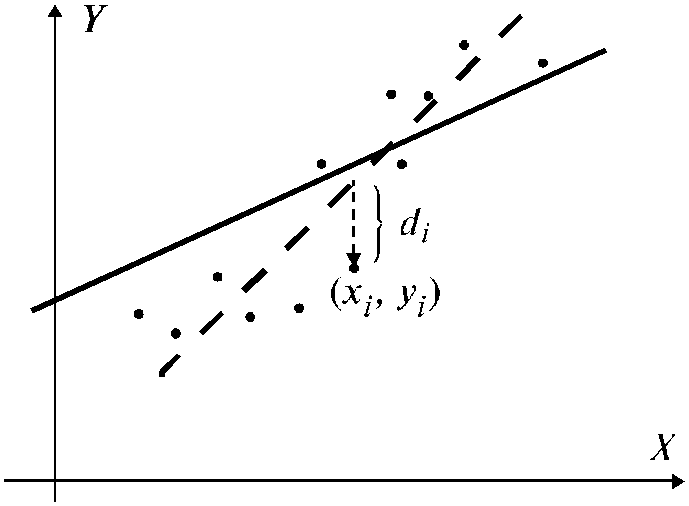
Рис. 5.2. Теоретическая регрессионная прямая наименьших квадратов

с указанным i-ым отклонением .

Прямая наименьших квадратов доставляет минимум S.

Пунктирная линия – прямая наименьших квадратов ,

сплошная линия – неизвестная теоретическая прямая .

Можно интерпретировать предсказанное значение двумя способами. При первом способе исследователь заинтересован в оценивании значения Y для индивидуума, у которого Х принимает значение х. В этой ситуации есть наилучшая оценка единственного значения Y, соответствующего Х = х. При втором подходе исследователь делает выводы о среднем значении Y для подвыборки, соответствующей значению Х = х. Тогда та же самая оценка будет наилучшей оценкой среднего значения при Х = х. Различие между этими двумя способами интерпретации важно, когда строятся доверительные интервалы (см. )