
- •Задачи для самостоятельного решения
- •2) Длину вектора .
- •2.2. Векторное и смешанное произведения векторов
- •Задачи для самостоятельного решения
- •Глава III. Основы аналитической геометрии
- •Уравнения прямой на плоскости
- •Задачи для самостоятельного решения
- •3.2. Взаимное расположение двух прямых на плоскости
- •Задачи для самостоятельного решения
- •3.3. Уравнения плоскости в пространстве
- •Задачи для самостоятельного решения
- •3.4. Взаимное расположение двух плоскостей
- •Задачи для самостоятельного решения
- •3.5. Уравнения прямой в пространстве
- •Задачи для самостоятельного решения
- •3.6. Взаимное расположение двух прямых в пространстве
- •Задачи для самостоятельного решения
- •3.7. Прямая и плоскость в пространстве
- •Задачи для самостоятельного решения
- •3.8. Кривые второго порядка
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
25. Найти канонические
уравнения прямой, проходящей через
точку
![]() параллельно:
параллельно:
а) оси ОХ; б) оси ОY; в) оси ОZ;
г) прямой
![]()
д) прямой
![]() .
.
26. Найти направляющий
вектор прямой
![]()
27. Привести к
каноническому виду прямую
![]()
-
Найти направляющие косинусы прямой
 .
. -
Найти параметрические уравнения прямой: а) проходящей через точку
 и параллельной вектору
и параллельной вектору
 ;
б) проходящей через точки
;
б) проходящей через точки
 и
и
 .
.
30. Составить канонические уравнения прямой, проходящей через две данные точки:
а)
![]()
![]()
б)
![]()
![]() .
.
31. Найти расстояние
от точки
![]() до прямой:
до прямой:
а)
![]() ;
;
б)
 ;
;
в)
![]()
32. Найти расстояние между скрещивающимися прямыми
![]()
![]()
3.6. Взаимное расположение двух прямых в пространстве
Пусть у прямых
![]() и
и
![]() известны направляющие векторы
известны направляющие векторы
![]() и
и
![]() соответственно.
соответственно.
Под углом
![]()
![]() между двумя прямыми в пространстве
понимается любой из двух смежных углов,
которые образуют прямые, проведенные
параллельно данным через какую-нибудь
точку пространства
между двумя прямыми в пространстве
понимается любой из двух смежных углов,
которые образуют прямые, проведенные
параллельно данным через какую-нибудь
точку пространства
![]() .
.
Угол
![]() находится исходя из формулы
находится исходя из формулы
![]() .
(3.32)
.
(3.32)
Условие параллельности прямых:
![]() .
(3.33)
.
(3.33)
Условие перпендикулярности прямых:
![]() .
(3.34)
.
(3.34)
Примеры
11. Найти величину угла между прямыми
![]() и
и
![]()
Р е ш е н и е.
Направляющий вектор первой прямой
![]() .
Находим направляющий вектор
.
Находим направляющий вектор

![]() ,
т. е.
,
т. е.
![]() .
.
![]() ,
,
![]() .
.
12. Установить взаимное расположение прямых:
а)
![]() и
и

![]() ;
;
б)
![]() и
и
![]() .
.
Р е ш е н и е. а) Выпишем направляющие векторы прямых:
![]() ,
,
![]() .
Так как координаты этих векторов
пропорциональны
.
Так как координаты этих векторов
пропорциональны
![]() ,
то данные прямые параллельны или
совпадают. Возьмем на первой прямой
какую-нибудь точку, например точку
,
то данные прямые параллельны или
совпадают. Возьмем на первой прямой
какую-нибудь точку, например точку
![]() .
Подставим ее координаты в уравнение
второй прямой:
.
Подставим ее координаты в уравнение
второй прямой:

Получаем
![]() из первого уравнения,
из первого уравнения,
![]() из второго,
из второго,
![]() из третьего. Так
как полученные значения различны, то
это означает, что точка
из третьего. Так
как полученные значения различны, то
это означает, что точка
![]() не принадлежит второй прямой. Прямые
не совпадают, значит, они параллельны;
не принадлежит второй прямой. Прямые
не совпадают, значит, они параллельны;
б) координаты
направляющих векторов
![]() и
и
![]() данных прямых не пропорциональны.
Следовательно, прямые либо пересекаются,
либо являются скрещивающимися. Выпишем
координаты точек, через которые проходят
данные прямые:
данных прямых не пропорциональны.
Следовательно, прямые либо пересекаются,
либо являются скрещивающимися. Выпишем
координаты точек, через которые проходят
данные прямые:
![]() и
и
![]() .
Проверим условие принадлежности двух
прямых одной плоскости:
.
Проверим условие принадлежности двух
прямых одной плоскости:
 =0,
=0,
 .
.
Следовательно, данные прямые являются скрещивающимися.
Задачи для самостоятельного решения
33. Найти величину острого угла между прямыми
а)
![]() и
и
![]() ;
;
б)
![]() и
и
![]()
34. Выяснить взаимное расположение прямых:
а)
![]() и
и
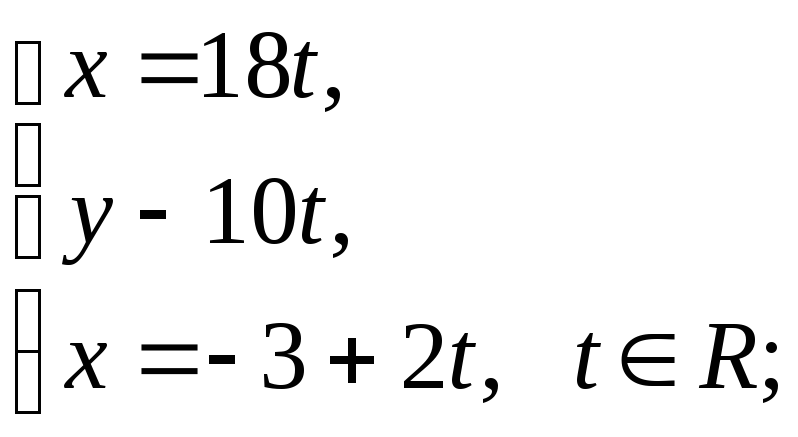
б)
![]() и
и
![]() .
.
35. Даны прямые
![]() ,
,
![]() .
При каком значении параметра m
прямые: а) перпендикулярны; б) параллельны?
.
При каком значении параметра m
прямые: а) перпендикулярны; б) параллельны?
3.7. Прямая и плоскость в пространстве
Величина угла
![]() между прямой (L)
между прямой (L)
![]() и плоскостью
и плоскостью
![]() определяется по формуле
определяется по формуле
![]() .
(3.35)
.
(3.35)
Условие параллельности прямой и плоскости:
![]()
![]()
![]() .
(3.36)
.
(3.36)
Условие перпендикулярности прямой и плоскости:
![]()
![]()
![]() .
(3.37)
.
(3.37)
Координаты точки пересечения прямой и плоскости находятся из решения системы уравнений:
![]() (3.38)
(3.38)
Примеры
13. Найти величину
угла между прямой
![]() и плоскостью
и плоскостью
![]()
Р е ш е н и е. Применим формулу (3.35):
![]()
![]() .
.
14. Установить взаимное расположение прямой и плоскости:
а)
 и
и
![]() ;
;
б)
![]() и
и
![]() .
.
Р е ш е н и е.
а) Имеем
![]() ,
,
![]() .
Прямая не перпендикулярна плоскости,
так как координаты векторов
.
Прямая не перпендикулярна плоскости,
так как координаты векторов
![]() и
и
![]() не пропорциональны:
не пропорциональны:
![]() .
.
Условие параллельности прямой и плоскости (3.36) также не выполняется:
![]() .
.
Следовательно, прямая пересекает плоскость. Параметрические уравнения прямой подставим в уравнение плоскости и найдем точку пересечения:
![]() .
.
б) Имеем
![]() ,
,
![]() .
.
Условие (3.36) параллельности прямой и плоскости выполняется:
![]() .
.
Следовательно, данная прямая параллельна плоскости или принадлежит ей.
Возьмем любую
точку
![]() прямой, например
прямой, например
![]() .
Подставим ее координаты в уравнение
плоскости:
.
Подставим ее координаты в уравнение
плоскости:
![]() .
.
Следовательно, прямая принадлежит плоскости.
