
- •Задачи для самостоятельного решения
- •2) Длину вектора .
- •2.2. Векторное и смешанное произведения векторов
- •Задачи для самостоятельного решения
- •Глава III. Основы аналитической геометрии
- •Уравнения прямой на плоскости
- •Задачи для самостоятельного решения
- •3.2. Взаимное расположение двух прямых на плоскости
- •Задачи для самостоятельного решения
- •3.3. Уравнения плоскости в пространстве
- •Задачи для самостоятельного решения
- •3.4. Взаимное расположение двух плоскостей
- •Задачи для самостоятельного решения
- •3.5. Уравнения прямой в пространстве
- •Задачи для самостоятельного решения
- •3.6. Взаимное расположение двух прямых в пространстве
- •Задачи для самостоятельного решения
- •3.7. Прямая и плоскость в пространстве
- •Задачи для самостоятельного решения
- •3.8. Кривые второго порядка
- •Задачи для самостоятельного решения
Задачи для самостоятельного решения
22. Найти величину острого угла между плоскостями:
а)
![]() и
и
![]() ;
;
б)
![]() и
и
![]() .
.
23. Найти расстояние между параллельными плоскостями:
а)
![]() и
и
![]() ;
;
б)
![]() и
и
![]() ;
;
в)
![]() и
и
![]() .
.
24. При каком значении
параметра
![]() заданные плоскости:
заданные плоскости:
1) параллельны; 2) перпендикулярны?
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,
![]() .
.
3.5. Уравнения прямой в пространстве
Общее уравнение прямой (как линия пересечения двух плоскостей):
 (3.26)
(3.26)
Система (3.26) определяет прямую только
в том случае, когда коэффициенты
![]() не пропорциональны коэффициентам
не пропорциональны коэффициентам
![]() .
.
Уравнение прямой, заданной точкой
![]() и направляющим вектором
и направляющим вектором
![]() (канонические
уравнения прямой):
(канонические
уравнения прямой):
![]() .
(3.27)
.
(3.27)
Параметрические уравнения прямой,
заданной точкой
![]() и направляющим вектором
и направляющим вектором
![]() :
:
 (3.28)
(3.28)
Уравнение прямой, проходящей через
две данные точки
![]() и
и
![]() :
:
![]() .
(3.29)
.
(3.29)
Расстояние от точки
![]() до прямой, заданной точкой
до прямой, заданной точкой
![]() и направляющим вектором
и направляющим вектором
![]() :
:
![]() .
(3.30)
.
(3.30)
Расстояние между скрещивающимися
прямыми, заданными точками
![]() и
и
![]() и направляющими векторами
и направляющими векторами
![]() и
и
![]() соответственно:
соответственно:
 .
(3.31)
.
(3.31)
Примеры
8. Общее уравнение прямой
![]()
преобразовать к каноническому виду; определить величины углов, образованные этой прямой с координатными осями.
Р е ш е н и е.
Для решения этой задачи надо знать
какую-либо точку прямой и ее направляющий
вектор
![]() .
Выберем точку на прямой следующим
образом: положим, например,
.
Выберем точку на прямой следующим
образом: положим, например,
![]() ,
тогда для определения абсциссы х
и ординаты у
у этой точки получим систему уравнений:
,
тогда для определения абсциссы х
и ординаты у
у этой точки получим систему уравнений:
![]()
Решая
систему, находим
![]() ,
,
![]() .
Итак, на прямой известна точка
.
Итак, на прямой известна точка
![]() . Направляющий
вектор прямой находим по формуле
. Направляющий
вектор прямой находим по формуле
 ,
,
![]() .
Тогда, согласно формуле (3.27)
.
Тогда, согласно формуле (3.27)
 или
или
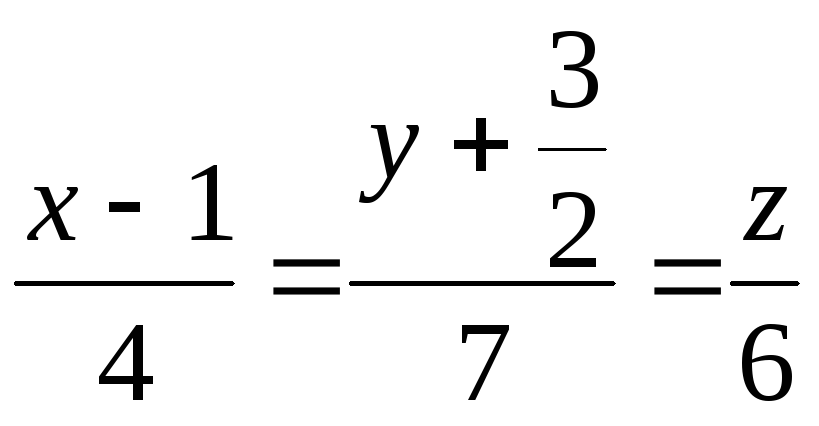 – канонические уравнения прямой.
– канонические уравнения прямой.
Направление прямой
задает вектор
![]() .
Он образует с координатными осями
.
Он образует с координатными осями
![]() углы
углы
![]() и
и
![]() соответственно. Находим эти углы по
формулам:
соответственно. Находим эти углы по
формулам:
![]() .
.
Получаем
![]() .
.
Заметим, что
равенство
![]() выполняется.
выполняется.
9. Составить
параметрические уравнения прямых,
проведенных через точку
![]() ,
в каждом из следующих случаев:
,
в каждом из следующих случаев:
а) прямая параллельна
прямой
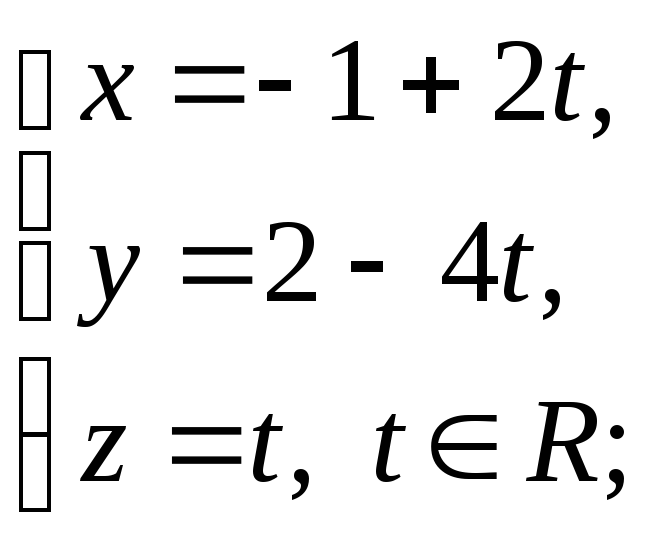
б) прямая параллельна
оси
![]() ;
;
в) прямая
перпендикулярна плоскости
![]() .
.
Р е ш е н и е.
а) Так как прямые параллельны, то они
имеют один и тот же направляющий вектор
![]() .
.
Согласно формуле (3.28), составляем параметрические уравнения прямой
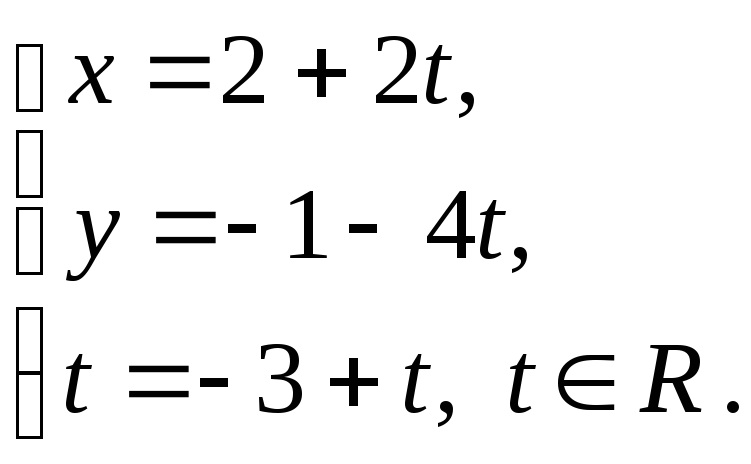
б) В качестве
направляющего вектора оси
![]() можно взять вектор
можно взять вектор
![]() совпадающий с ортом
совпадающий с ортом
![]() .
Искомые
уравнения прямой есть
.
Искомые
уравнения прямой есть
 т. е.
т. е.

в) Вектор
![]() перпендикулярен плоскости
перпендикулярен плоскости
![]() .
.
Следовательно, в
качестве направляющего вектора прямой
можно взять вектор
![]() т. е.
т. е.
![]() .
Тогда параметрические уравнения прямой
примут вид
.
Тогда параметрические уравнения прямой
примут вид

10. Составить
канонические уравнения прямой, проходящей
через точку
![]() параллельно:
параллельно:
а) вектору
![]() ;
;
б) прямой
![]()
Р е ш е н и е.
а) В качестве направляющего вектора
прямой, проходящей через точку
![]() ,
возьмем вектор
,
возьмем вектор
![]() ,
равный вектору
,
равный вектору
![]() ,
т. е.
,
т. е.
![]() .
Тогда по формуле (3.27) канонические
уравнения прямой примут вид
.
Тогда по формуле (3.27) канонические
уравнения прямой примут вид
![]() .
.
б) Направляющий
вектор
![]() данной прямой находим по формуле
данной прямой находим по формуле
 т. е.
т. е.
![]() .
.
Так как данная
прямая и искомая параллельны между
собой, то в качестве направляющего
вектора
![]() искомой прямой можно взять вектор
искомой прямой можно взять вектор
![]() ,
т. е.
,
т. е.
![]() .
Получаем канонические уравнения:
.
Получаем канонические уравнения:
![]() .
.
