Из пропорции найдем значение , которое не совпадает с предыдущим значением.

Следовательно, векторы и не будут коллинеарными ни при каких значениях .

2) Запишем условие перпендикулярности двух векторов: , или , 7.

Откуда .

Следовательно, при векторы и будут перпендикулярными.

6. Даны векторы , , . Найти проекцию вектора на вектор .

Р е ш е н и е. В нашем случае , , .

Тогда требуемая проекция находится по формуле (2.8)

7. Даны векторы , , , в некотором базисе. Показать, что векторы образуют базис, и найти координаты вектора в этом базисе.

Р е ш е н и е. Проверим условие, при выполнении которого векторы образуют базис. Для этого вычислим определитель матрицы, составленной из координат векторов . Имеем

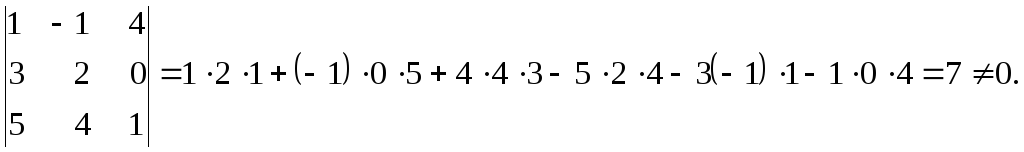
Следовательно, векторы образуют базис.

Пусть вектор в базисе имеет координаты т. е. . Вектор является линейной комбинацией векторов :

. Полученное равенство запишем в координатной форме:

.

Преобразуем правую часть:

,

.

Из равенства векторов следует равенство их координат. Получаем систему линейных уравнений относительно неизвестных :

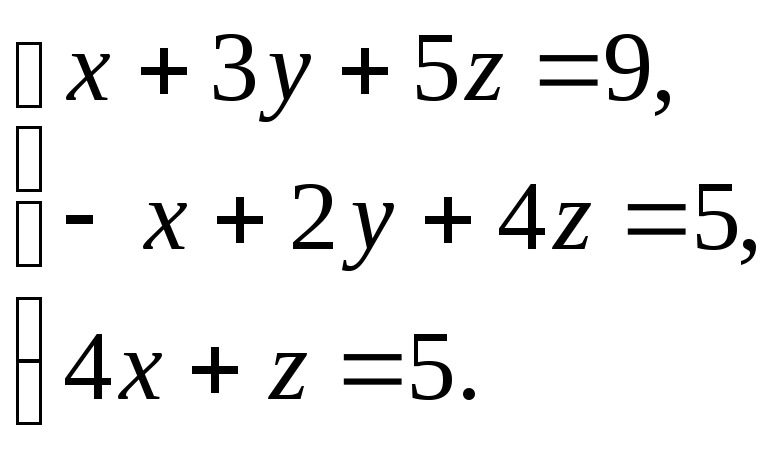
Решая эту систему любым из известных способов, находим

.

Следовательно, .

Задачи для самостоятельного решения

1. Показать геометрически, что .

2. Найти в треугольнике АВС точку О, для которой .

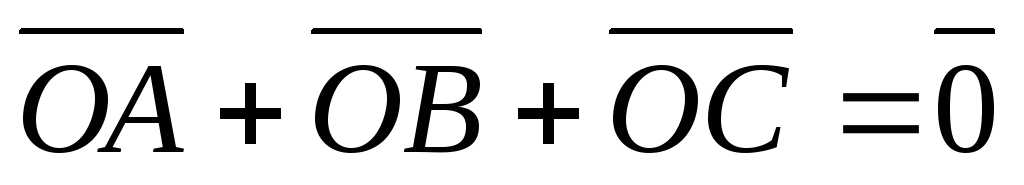3. Точка О – точка пересечения диагоналей параллелограмма АВСD. Чему равняются векторы:

1) 2) ; 3) ?

4. Даны координаты точек , . Найти:

1) длину вектора ;

2) Длину вектора .

5. Вычислить скалярные произведения .

6. При каком значении параметра вектор перпендикулярен вектору ?

7. Найти угол между векторами и , если , .

8. Известно, что .

Вычислить: 1) ; 2) ; 3) ; 4) .

9. Даны векторы , . Требуется:

1) определить перпендикулярность векторов и ;

2) вычислить координаты вектора ;

3) найти угол между векторами и ;

4) найти проекции , , ;

5) вычислить направляющие косинусы вектора .

10. Определить, при каких значениях параметров векторы и :

1) коллинеарны;

2) перпендикулярны.

11. На плоскости даны векторы , . Найти координаты вектора в базисе .

12. В пространстве даны векторы , в некотором базисе.

Показать, что векторы образуют базис, и найти координаты вектора в этом базисе.

2.2. Векторное и смешанное произведения векторов

Пусть , , .

Векторным произведением векторов и называется вектор, обозначаемый или , удовлетворяющий условиям:

1) где – угол между векторами и ; (2.9)

2) , ;

3) упорядоченная тройка векторов – правая, т. е. если смотреть из конца вектора , то кратчайший поворот от вектора к вектору осуществляется против хода часовой стрелки (в противном случае тройка называется левой).

Если хотя бы один из векторов и нулевой, то полагают .

Векторное произведение в координатной форме:

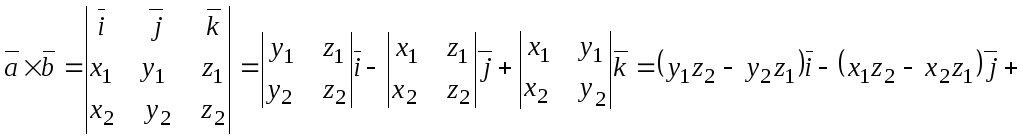
+. (2.10)

Ненулевые векторы и коллинерны тогда и только тогда, когда их векторное произведение равняется нулевому вектору; . (2.11)

Геометрический смысл векторного произведения: длина вектора векторного произведения векторов и численно равняется площади параллелограмма, построенного на векторах и , приведенных к общему началу.

Смешанным произведением трех векторов называется число, обозначаемое или и равное скалярному произведению вектора на вектор : .

Смешанное произведение векторов , , в координатной форме:

. (2.12)

Ненулевые векторы компланарны тогда и только тогда, когда их смешанное произведение равняется нулю .

Геометрический смысл смешанного произведения: смешанное произведение трех векторов численно равняется объему параллелепипеда, построенного на векторах (приведенных к общему началу), взятому со знаком «+», если тройка – правая, и взятому со знаком «–», если тройка – левая.

Примеры

8. Вычислить , если известно, что , , .

Р е ш е н и е. Согласно свойствам векторного произведения, получаем:

=.

Следовательно, .

По формуле (2.9) находим модуль векторного произведения:

Тогда .

9. Даны векторы . Найти их векторное произведение, синус угла между ними и площадь параллелограмма, построенного на этих векторах.

Р е ш е н и е. Применим формулу(2.10):

.

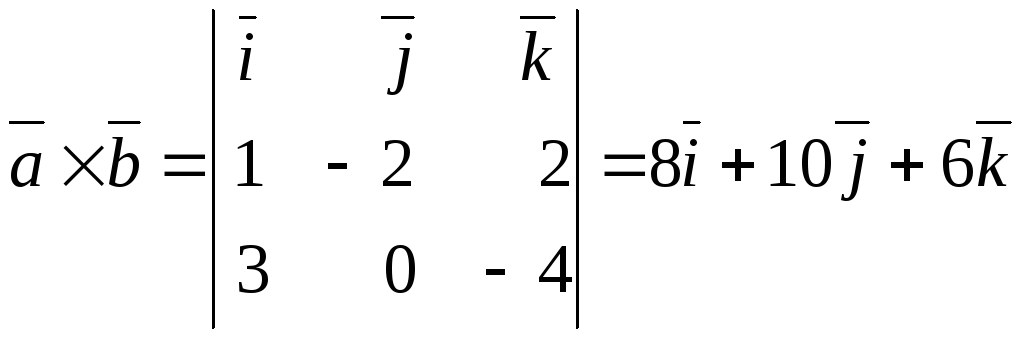Находим площадь параллелограмма:

.

Найдем синус угла между данными векторами:

10. Вычислить смешанное произведение если .

Р е ш е н и е. Согласно свойствам смешанного произведения, получаем:

= Так как , то

11. Доказать, что векторы , компланарны.

Р е ш е н и е. Проверим условие компланарности . Найдем смешанное произведение этих векторов по формуле (2.12):

.

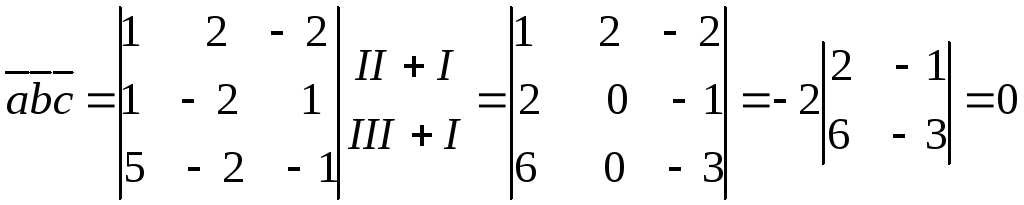С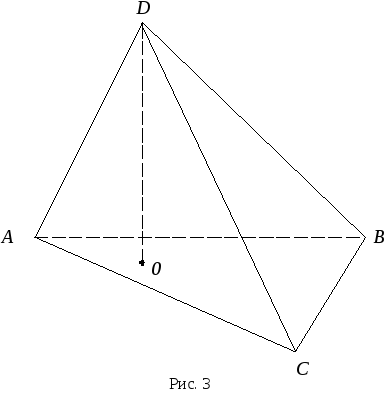 ледовательно, векторы – компланарны.

12. Даны вершины пирамиды . Найти длину высоты, опущенной из вершины D на грань АВС (рис. 3).

Р е ш е н и е. Так как объем V пирамиды есть , то , где – длина высоты пирамиды, S – площадь основания.

Находим ,   .

=

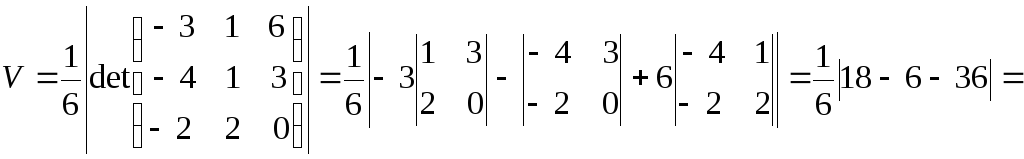
Находим площадь основания:

.

Следовательно, .