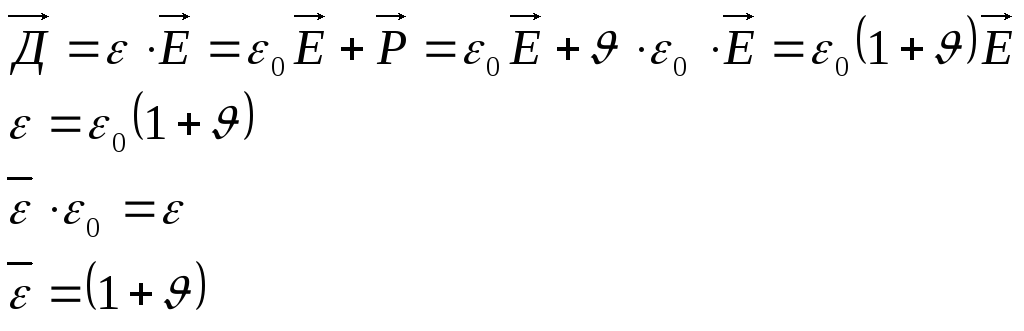- •Основы векторного анализа
- •Криволинейные ортогональные системы координат
- •Запись операторов векторного анализа в обобщённой криволинейной системе координат.
- •Основные величины макроскопической электродинамики, напряжённость поля.
- •Закон кулона
- •Вектора индукции поля
- •Силовые линии поля
- •Уравнение обобщающее закон кулона теорема Гаусса
- •Обобщение закона электромагнитной индукции
- •Эсп в проводниках и диэлектриках
- •Вычисление характеристик эп по заданным зарядам
- •Дифференциальные уравнения для потенциала
- •Метод зеркальных изображений
- •Метод решения прямой задачи электростатики
- •Граничные условия на границе раздела двух диэлектриков Определение объёмной плотности свободного заряда.
- •Постоянный электрический ток
- •Сторонние силы
- •Закон Ома
- •Работа и мощность тока
- •Обобщённый закон Ома (закон Ома для неоднородного участка цепи)
- •Правило Кирхгофа
- •Магнитное поле
- •Магнитное поле кольцевого проводника
- •Закон Ампера
- •Магнитное поле движущегося заряда
- •Сила Лоренца
- •Магнитное поле соленоида
- •Явления связанные с законом электромагнитной индукции
- •Токи Фуко
- •Индуктивность
- •Явление самоиндукции
- •Явление взаимоиндукции
- •Расчёт коэффициентов взаимоиндукции тороидального трансформатора.
- •Принцип действия электрического трансформатора
- •Переходные процессы при замыкании и размыкании lr цепи
- •Процессы при отключении rl цепи
- •Энергия электрического и магнитного полей.
- •Энергия магнитного поля
- •Эффект Холла
- •Магнитные свойства вещества
- •Явление диа и пара магнетизма
- •Мп в веществе
- •Ферромагнетики
- •Уравнение Максвелла как обобщение электричества и магнетизма.
- •Колебания и волны
- •Механические гармонические колебания
- •Гармонический осциллятор
- •Колебательный контур
- •Решение дифференциального уравнения свободных затухающих колебаний
- •Сложение гармонических колебаний одного направления
- •Сложение взаимно перпендикулярных колебаний
- •Вынужденные колебания
- •Ачх вынужденных колебаний
- •Переменный эт
- •Цепь содержащая r l c элементы
- •Явление резонанса напряжений
- •Явление резонанса токов
- •Мощность в цепи переменного тока.
Эсп в проводниках и диэлектриках
Рассмотрим поведение ЭСП которое может быть описано
![]()
![]()
Предполагаем что некоторый не подвижный заряд находится в проводнике и естественно создаёт ЭП. Определим напряжённость этого поля внутри проводника. Величину напряжённости ЭСП можно получить из выше представленного уравнения описывающего закон Ома в дифференциальной форме.
![]()
Так как проводник характерен тем, что
его удельная проводимость отлична от
нуля, а поле является электростатическим,
то
![]() ,
то можем сделать вывод, что напряжённость
ЭСП внутри проводника равна нулю.
,
то можем сделать вывод, что напряжённость
ЭСП внутри проводника равна нулю.
Определим как линии напряжённости ЭСП будут относиться по отношению к поверхности проводника. Рассмотрим некоторый участок dL на поверхности проводника. Разность потенциалов между двумя точками находящихся на расстоянии dL друг от друга мы определим как dφ. dφ – может быть определено как:
![]()
Таким образом линии напряжённости
перпендикулярны по отношению к поверхности
проводника. Предполагаем что вектор
напряжённости ЭСП не перпендикулярен
по отношению к поверхности проводника,
тогда данный вектор
![]() можно разложить на 2 составляющие на Еn
и Еτ. Наличие Еτ говорит о том что имеется
сила.
можно разложить на 2 составляющие на Еn
и Еτ. Наличие Еτ говорит о том что имеется
сила.
![]()
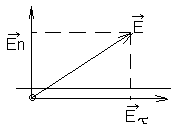
которая заставляет двигаться заряд по поверхности проводника. Отсюда видно, что вектор ЭСП нормален по отношению к поверхности проводника. Так как потенциал на поверхности проводника в случае ЭСП везде одинаковый, то металлическую поверхность можно назвать эквипотенциальной поверхностью.
Поведение ЭСП внутри диэлектрика.
Внутри диэлектрика отсутствует свободный электрический заряд, но молекулы диэлектрика можно представить в виде связного электрического заряда который в свою очередь легко смоделировать в виде диполей, то есть двух жёстко связанных положительных и отрицательных зарядов находящихся на малом расстоянии друг от друга. Под действием внешнего ЭП диэлектрик поляризуется. Этот процесс состоит в том, что диполи начинают во внешнем ЭП разворачиваться вдоль линий напряжённости внешнего ЭП. При этом положительный заряд движется по полю, а отрицательный против поля.
Все диэлектрики можно разделить на полярные и не полярные. У полярных центры тяжести положительных и отрицательных зарядов не совпадают и в отсутствии внешнего ЭП данные связные заряды обладают собственным дипольным моментом. К полярным относятся молекулы не симметричной структуры. У не полярных молекулярные центры тяжести положительных и отрицательных зарядов совпадают и в отсутствии внешнего ЭП не полярные молекулы не обладают собственным дипольным моментом. Причём такие диполи можно представить в виде положительных и отрицательных зарядов связанных упругой связью, в то время как у полярных молекул связь жёсткая.
Под действие внешнего ЭП не полярные молекулы деформируются и так же как и полярные молекулы выстраиваются по полю в процессе поляризации не полярные молекулы приобретают собственный дипольный момент.
В результате процесса поляризации на
внешней поверхности диэлектрика
появляется не скомпенсированный связный
электрический заряд. Поле данного
связного заряда
накладывается на
внешнее поле и в результате ЭП внутри
диэлектрика уменьшается. Поле внутреннее
меньше поля внешнего в
![]() раз.
раз.
Можно определить взаимосвязь между объёмной плотностью связного заряда и характеристикой ЭП. Вектор элементарного смещения равен:
![]()
![]() - вектор поляризации.
- вектор поляризации.
Взяв дивергенцию от левой и правой части получаем:
![]()
И учитывая уравнение обобщающее закон кулона
![]()
![]() - объёмная плотность свободного заряда
созданного внешним ЭП.
- объёмная плотность свободного заряда
созданного внешним ЭП.
Из этого следует:
![]()
![]()
В случае диэлектрика происходит уменьшение напряжённости ЭП по сравнению с полем вакуума из-за наличия связного заряда находящегося внутри диэлектрика. Можно показать, что между связным зарядом и вектором поляризации существует следующая взаимосвязь.
![]()
![]() - объёмная плотность связного заряда.
- объёмная плотность связного заряда.
![]()
V – объём находящийся внутри замкнутой поверхности S. Из данного выражения следует что отрицательный связный заряд создаёт положительный поток вектора поляризации и наоборот положительный связный заряд создаёт отрицательный поток вектора поляризации.
Вектор поляризации сонаправлен с вектором направления ЭП и данные вектора связаны следующим соотношением:
![]()
![]() - диэлектрическая восприимчивость
вещества.
- диэлектрическая восприимчивость
вещества.
Учитывая введённую связь между
![]() и
и
![]() можно ввести взаимосвязь между
диэлектрической восприимчивостью и
абсолютной диэлектрической проницаемостью:
можно ввести взаимосвязь между
диэлектрической восприимчивостью и
абсолютной диэлектрической проницаемостью: