Закон кулона

Закон определяющий силу взаимодействия точечных электрических зарядов экспериментально был установлен Кулоном.

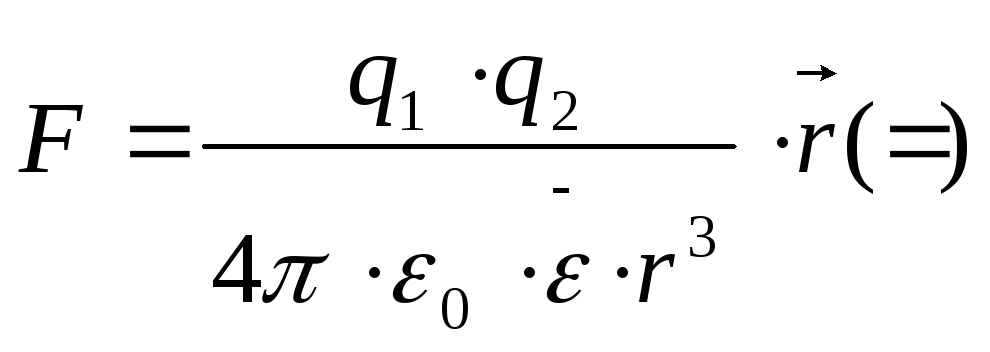
где: и - величины взаимодействующих зарядов находящихся на расстоянии r друг от друга. - диэлектрическая постоянная вакуума =8.85. - относительная диэлектрическая проницаемость среды.

Величина показывающая во сколько раз напряженность электрического поля в данной среде отличается от напряжённости в вакууме.

где: - абсолютная диэлектрическая проницаемость среды.

С помощью закона кулона и определения напряжённости электрического поля можно определить напряжённость электростатического поля созданного в некоторой среде точечным зарядом q на расстоянии r от данного заряда.

Исходя из полученного выражения для напряжённости электростатического поля можно утверждать что силовые линии электростатического поля ( линии касающиеся в каждой точке вектора напряженности) выходят из положительного заряда входят в отрицательный заряд.

Закон кулона справедлив вплоть до.

В природе существуют иные силовые поля электрического происхождения то есть которые обусловлены наличием заряда. К таким силовым полям относится магнитное поле. Характерной особенностью магнитного поля является то что данное силовое поле действует только на движущиеся электрические заряды (движущиеся относительно некоторой инерциальной системы отсчёта), а так же данное поле действует на связные магнитные заряды. Связным называется такой заряд который в сколь угодно малом объеме содержит одновременно заряды двух знаков. Если заряды в сколь угодно малом объёме могут содержать только положительные или только отрицательные знаки, то такие заряды называются свободными. Электрические заряды могут быть как свободными так и связными. Свободных магнитных зарядов в природе нет. Отличительной особенностью электрического поля от магнитного поля является то что магнитное поле как генерируется так и может быть обнаружено по силовому воздействию лишь на связные магнитные и движущиеся электрические заряды. Электрическое поле создается неподвижными так и движущимися электрическими зарядами, так и может быть обнаружено по силовому воздействию на данный вид зарядов. Силовой характеристикой магнитного поля является напряжённость.

Вектора индукции поля

Внутренние электромагнитные процессы в веществе обычно взаимно уравновешены по этому обычные вещества сами по себе не создают макроскопического поля. Исключение составляют лишь некоторые среды например (ферромагнетики и сегнетоэлектрики) и ряд других веществ у которых внутренние процессы взаимно не уравновешены. Из ферромагнетиков выполняют постоянные магниты и сердечники трансформаторов. В обычных веществах при воздействии внешнего электрического поля и магнитного поля внутренняя уравновешенность нарушается. Так например при внесении диэлектрика во внешнее электрическое поле происходит некоторая деформация и переориентация молекул диэлектрика во внешнем электрическом поле. Данный процесс получил название поляризации диэлектрика. Молекулы диэлектрика можно условно смоделировать в виде диполя то есть связного электрического заряда который имеет одинаковые по величине но разные по знаку заряды, связанные либо жёсткой либо упругой связью. Данная модель молекулы правомерна потому, что в целом молекула диэлектрика нейтральна и состоит из положительного ядра и отрицательных электронов. Суммарный заряд которых равен заряду ядра. Поэтому молекулы диэлектрика можно определить как связные заряды моделируемые с помощью диполя. Основной характеристикой диполя является дипольный электрический момент, который определяется как:

q – заряд диполя; - вектор равный плечу диполя и направленный от отрицательного к положительному заряду.

Рассмотрим следующий пример: поместим между пластинами плоского конденсатора (устройство предназначенное для накопления электрического заряда и концентрации электрического поля) брусок диэлектрика. Конденсатор создает внешнее электрическое поле в данное внешнее электрическое поле попадает диэлектрик. Под воздействием этого поля молекулы диэлектрика поляризуются, то есть ориентируются вдоль внешнего электрического поля.

В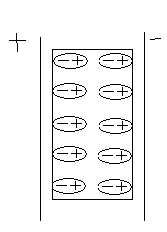 результате на границах этой пластины появляются не скомпенсированные отрицательные и положительные связные заряды. Связные заряды создают свое электрическое поле которое накладываясь на вешнее электрическое поле меняет поле в диэлектрике. Для того что бы измерить поле внутри диэлектрика, необходимо внутри диэлектрика вырезать игольчатую полость ориентированную вдоль внешнего электрического поля. В этом случае связные заряды на концах данной игольчатой полости не будут влиять на поле измеряемое в диэлектрике и внутрь данной игольчатой полости внести пробный положительный заряд. Опыт показал что напряжённость электрического поля внутри диэлектрика соотносится с напряжённостью электрического поля созданного заряженным конденсатором следующим образом:

- напряженность поля внутри диэлектрика; - внешнее электрическое поле созданное заряженным конденсатором; - относительная диэлектрическая проницаемость диэлектрика.

Таким образом как показал эксперимент поле внутри диэлектрика уменьшается в раз по сравнению с внешним электрическим полем а саму диэлектрическую проницаемость можно трактовать как величину показывающую во сколько раз поле внутри диэлектрика меньше внешнего электрического поля. Сила действующая на некоторый заряд g внутри диэлектрической среды с относительной диэлектрической проницаемостью .

Если в диэлектрической среде вырезать доскообразную полость перпендикулярную внешнему полю, то сила действующая на некоторый заряд g помещённый в данную доскообразную полость определяется как:

Таким образом напряжённость поля в доскообразной полости совпадает с величиной внешнего поля.

Напряжённость электрического поля не является исчерпывающей характеристикой электрического поля. Действительно данная величина в диэлектрике зависит от диэлектрической проницаемости и зависит от связных зарядов которые отчасти образуют данное поле.

Напряжённость электрического поля в диэлектрике определяет не только вид поля связи зарядов а так же линии напряженности могут претерпевать разрыв на границе раздела двух диэлектриков. Поэтому появилась необходимость введения ещё одной характеристики поля а именно индукции электрического поля. Принципиальное отличие индукции от напряжённости состоит в том что линии индукции начинаются лишь на свободных зарядах в то время как линии напряжённости могут начинаться как на свободных так и на связных зарядах. Таким образом силовые линии индукции электрического поля создаются свободными зарядами, но в то время как данные свободные заряды находятся в поле связных зарядов причём поле связных зарядов заставляет перераспределяться свободные заряды. Индукции ( - )

В том случае если вектор напряжённости электрического поля в среде со направлен с вектором ,то (↑↑) данная среда называется изотропной. Относительная диэлектрическая проницаемость не зависит от выбора того или иного направления в данной среде и между компонентами индукции электрического поля и напряжённости существует следующая взаимосвязь:

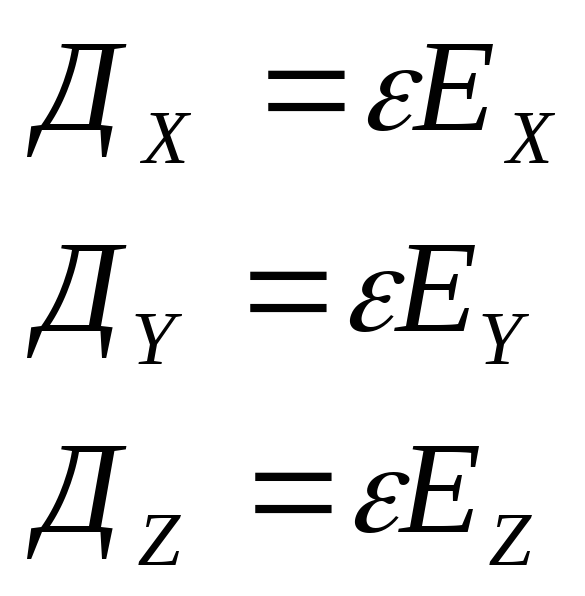
Если не со направлено с то среда является анизотропной в этом случае диэлектрическая проницаемость среды будет зависеть от выбора направления в данной среде.

Взаимосвязь между компонентами вектора электрической индукции и вектора напряжённости вычисляется так:

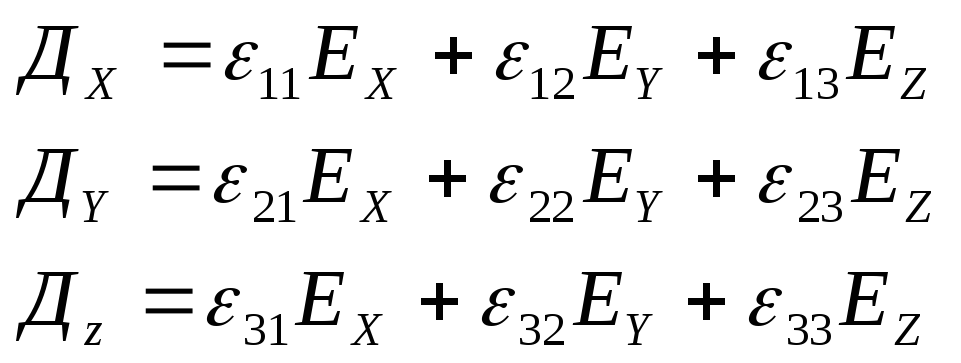
В векторной форме:

где: - тензор диэлектрической проницаемости среды =

Введём ещё одну характеристику электрического поля определяющую поляризацию диэлектрика. Данная величина получила название вектора поляризации и данная величина связана с вектором индукции (с вектором электрического смещения).

- вектор поляризации

Его можно ввести и другим образом. Если рассмотрим бесконечно малый объём ∆V диэлектрика находящегося во внешнем электрическом поле и определим суммарный дипольный момент ∆Р данного объёма, то величина равная отношению

получила название поляризации.

Таким образом вектор поляризации – плотность эклектического момента величина характеризующая некоторую точку среды.

Для магнитного поля можно ввести аналогичную силовую характеристику. Рассмотрим некоторую рамку с током закреплённую относительно некоторой оси проходящей через ось симметрии рамки. Если данную рамку поместить во внешнее магнитное поле характеризуемое напряжённостью . Данная рамка начнёт вращаться во внешнем магнитном поле вокруг оси. Это говорит о том что на рамку действует момент пары сил, причём эти силы обусловлены действуем магнитного поля.

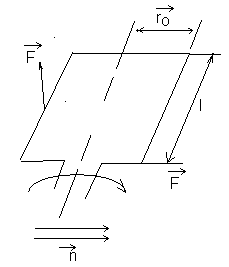- радиус вектор от оси к стороне длинной l; - сила действующая со стороны магнитного поля на элемент рамки длинной l.

Величина равная модулю

(где I- ток протекающий по рамке; L – длинна элемента рамки) получило название модуля магнитного смещения (индукции) магнитного поля.

Сила действующая со стороны внешнего магнитного поля на единицу длины элемента с током можно ввести следующим образом. Рассмотрим два бесконечных проводника находящихся на расстоянии r друг от друга по которым протекает ток I1 и I2, если токи со направлены, то два проводника начнут притягиваться друг к другу. Противо-направлены они отталкиваются друг от друга. Это силовое взаимодействие обусловлено следующим: один из проводников с током создает магнитное поле а другой это магнитное поле обнаруживает по силовому воздействию со стороны магнитного поля созданного первым проводником. Детальный анализ данной системы показал что сила взаимодействия двух таких проводников в вакууме может быть определена следующим образом:

- магнитная проницаемость вакуума =

Между напряжённостью магнитного поля и индукцией магнитного поля в вакууме существует взаимосвязь.

В некоторой среде эта взаимосвязь

- относительная магнитная проницаемость среды.

-абсолютная проницаемость среды.

- является векторной величиной причём направление данного вектора на примере рамки с током может быть определено так:

Измеряется в Теслах [Тл]

Подобно тому как мы ввели вектор поляризации электрического поля можно ввести вектор намагниченности. Связать его с вектором магнитной индукции.

Вектор намагниченности

- суммарный магнитный момент элементарного объёма магнетика .

Вектор намагниченности определяется как плотность магнитного момента.