Колебательный контур

Система в которой происходят электрические колебания (период изменения тока) заряда или напряжения наблюдается в таком гармоническом асциляторе как колебательный контур. Простейший колебательный контур представляет собой цепи содержащие индуктивности и ёмкости и в том случае если ёмкость будет первоначально заряжена, то колебание будет происходить за счёт энергии ЭП конденсатора. При этом в процессе колебания будет происходить период изменения энергии ЭП и энергии магнитного поля при этом будет наблюдаться перход энергии ЭП в энергию МП и на оборот. И в отсутствии потерь полная энергия колебательной системы будет оставаться постоянной. Реальной колебательной системой является система с потерями.

Реальная колебательная система с потерями:

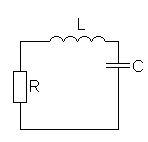
Дифференциальное уравнение свободных колебаний которые происходят в данной электрической цепи можно вывести исходя из закона Ома:

- падение напряжения на сопротивление R;

- напряжение на ёмкости;

- ЭДС самоиндукции возникающее в данном контуре при разряде конденсатора.

Данное уравнение можно записать для величины заряда на конденсаторе. Q – заряд который будет меняться с течением времени.

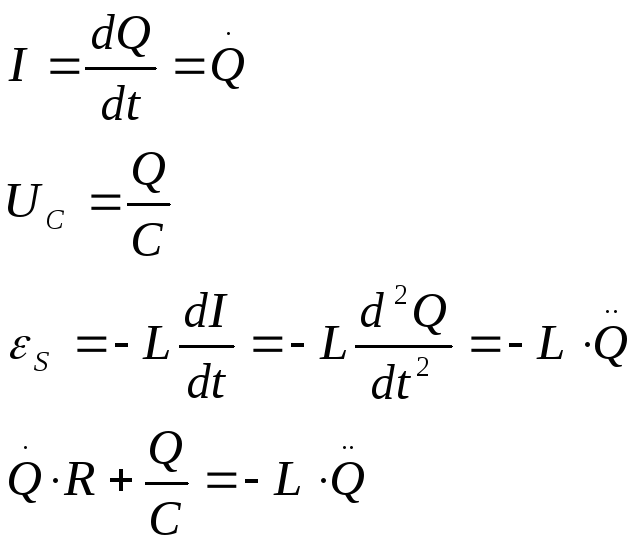
(1)

(1) – описывает свободные затухающие колебания то есть описывает колебания которые происходят в системе с потерями.

- коэффициент затухания.

Отсюда:

(2)

В том случае если потери в колебательном контуре отсутствуют (R=0) то схема преобразовывается.

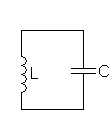
Дифференциальное уравнение для данного колебательного контура для величины заряда q:

Это дифференциальное уравнение получатся из уравнение (2) данное уравнение совпадает с уравнением (*). Поэтому (циклическая частота собственных не затухающих колебаний)

- циклическая частота собственных колебаний не затухающих.

Решением данного дифференциального уравнения:

- амплитуда заряда на ёмкости.

Определить закон изменения заряда на ёмкости от времени можно как закон изменения тока в цепи:

- амплитуда тока в данной электрической цепи.

Как видно ток по фазе опережает величину заряда на так же исходя из выражения для заряженной ёмкости можно определить напряжение на ёмкости:

- амплитуда напряжения на ёмкости

Как видно напряжение на ёмкости совпадает по фазе с зарядом на ёмкости. Введя циклическую частоту свободный циклических колебаний дифференциальное уравнение свободных затухающих колебаний можно записать:

(3)

При отсутствии затуханий полная энергия колебательного контура остается постоянной, но в процессе колебаний периодически происходит перераспределение энергии между её электрическими составляющими (энергия электрического поля конденсатора) и магнитной составляющей (энергия МП катушки индуктивности)

Решение дифференциального уравнения свободных затухающих колебаний

Найдём решение дифференциального уравнения свободных затухающих электрических колебаний. Решением уравнения (3).

(4)

Найдём первую и вторую производные от функции с учётом её представления в виде (4)

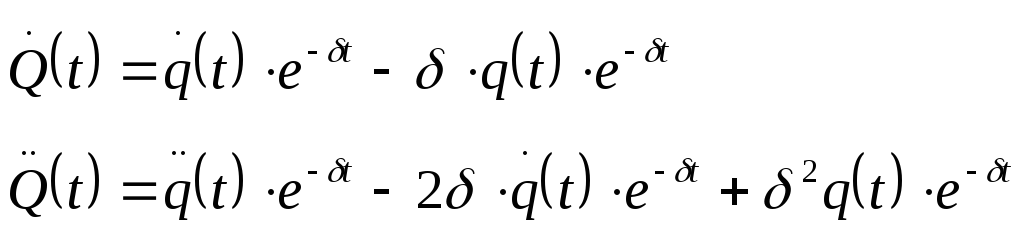
Полученное уравнение подставим в выражение (3)

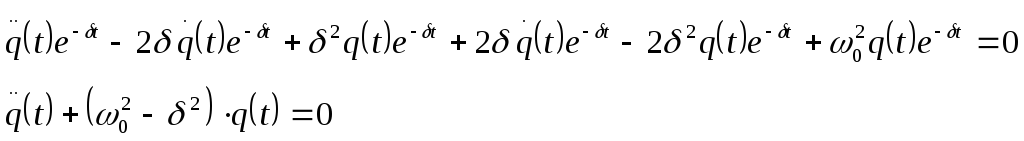
Данное уравнение по форме совпадает с уравнением (*), то есть с уравнением свободных колебаний. Следовательно решением данного уравнения является:

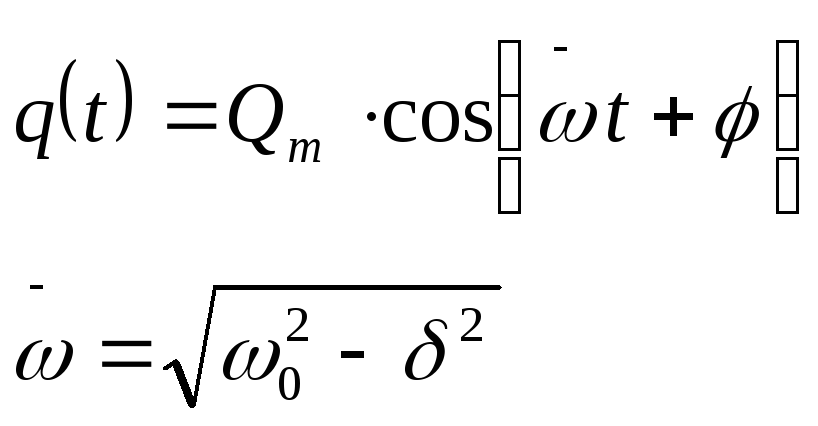
Учитывая что первоначальное решение:

Получаем что решение дифференциального уравнения свободных затухающих колебаний:

Полученное выражение даёт возможность построить график свободных затухающих колебаний.

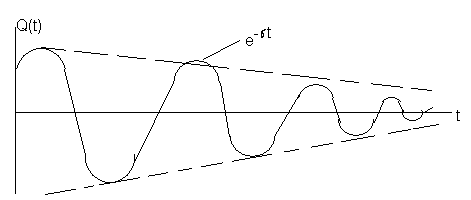
Таким образом из выражения описывающего свободные затухающие колебания следует что амплитуда этих колебаний с течением времени будет изменяться по экспоненциальному закону. Затухающие колебания периодическими не являются, но при малых затуханиях

Данное колебание можно считать почти периодическим. При этом под периодом данных колебаний понимают временной интервал между соседними максимумами и минимумами.

- период собственных электрических колебаний.

Данное равенство справедливо для малых затуханий. В качестве характерного колебания вводится величина – дикримент.

- дикримент.

- логарифмический дикримент затухания.

В качестве характеристики колебательного контура вводится величина называемая добротностью и обозначается . В самом общем случае добротность может определяться как отношение запасённой в колебательном контуре к энергии потерь. Можно показать что между добротностью и логарифмическим дикриментом затухания существует следующая взаимосвязь

- число колебаний через которое амплитуда колебания уменьшается в раз.

- время релаксации ( время за которое амплитуда колебаний уменьшается в раз)

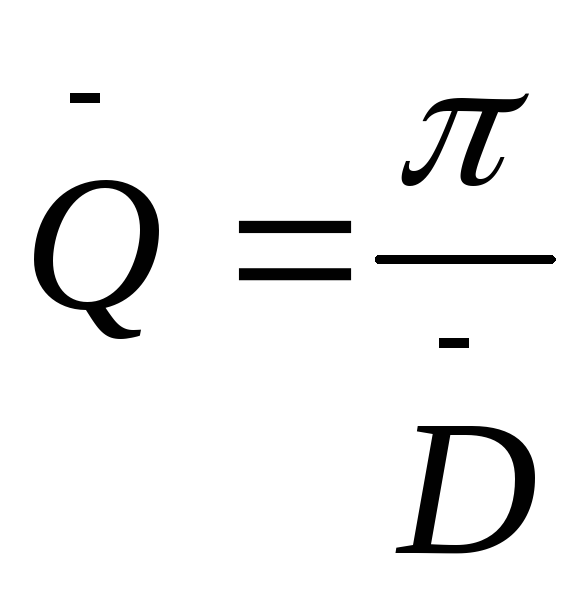
При малых затуханиях

- период собственных электрических колебаний, учитывая что

Из полученного выражения добротность обратно пропорциональна коэффициенту затухания.