
- •Основы векторного анализа
- •Криволинейные ортогональные системы координат
- •Запись операторов векторного анализа в обобщённой криволинейной системе координат.
- •Основные величины макроскопической электродинамики, напряжённость поля.
- •Закон кулона
- •Вектора индукции поля
- •Силовые линии поля
- •Уравнение обобщающее закон кулона теорема Гаусса
- •Обобщение закона электромагнитной индукции
- •Эсп в проводниках и диэлектриках
- •Вычисление характеристик эп по заданным зарядам
- •Дифференциальные уравнения для потенциала
- •Метод зеркальных изображений
- •Метод решения прямой задачи электростатики
- •Граничные условия на границе раздела двух диэлектриков Определение объёмной плотности свободного заряда.
- •Постоянный электрический ток
- •Сторонние силы
- •Закон Ома
- •Работа и мощность тока
- •Обобщённый закон Ома (закон Ома для неоднородного участка цепи)
- •Правило Кирхгофа
- •Магнитное поле
- •Магнитное поле кольцевого проводника
- •Закон Ампера
- •Магнитное поле движущегося заряда
- •Сила Лоренца
- •Магнитное поле соленоида
- •Явления связанные с законом электромагнитной индукции
- •Токи Фуко
- •Индуктивность
- •Явление самоиндукции
- •Явление взаимоиндукции
- •Расчёт коэффициентов взаимоиндукции тороидального трансформатора.
- •Принцип действия электрического трансформатора
- •Переходные процессы при замыкании и размыкании lr цепи
- •Процессы при отключении rl цепи
- •Энергия электрического и магнитного полей.
- •Энергия магнитного поля
- •Эффект Холла
- •Магнитные свойства вещества
- •Явление диа и пара магнетизма
- •Мп в веществе
- •Ферромагнетики
- •Уравнение Максвелла как обобщение электричества и магнетизма.
- •Колебания и волны
- •Механические гармонические колебания
- •Гармонический осциллятор
- •Колебательный контур
- •Решение дифференциального уравнения свободных затухающих колебаний
- •Сложение гармонических колебаний одного направления
- •Сложение взаимно перпендикулярных колебаний
- •Вынужденные колебания
- •Ачх вынужденных колебаний
- •Переменный эт
- •Цепь содержащая r l c элементы
- •Явление резонанса напряжений
- •Явление резонанса токов
- •Мощность в цепи переменного тока.
Криволинейные ортогональные системы координат
При описании многих физических процессов удобно использовать криволинейные системы координат (не декартовы). Так как при описании тел цилиндрической формы удобней использовать цилиндрическую систему координат и сферическую которые строятся на основе декартовой системы координат.
Цилиндрическая система может быть получена на основе декартовой следующим образом. Предположим, что есть некоторая точка определённая в декартовой системе координат. Построим цилиндр таким образом что бы основание цилиндра лежало в плоскости XOY декартовой системы координат, на основании которой строим, а точка Р на боковой поверхности данного цилиндра.
С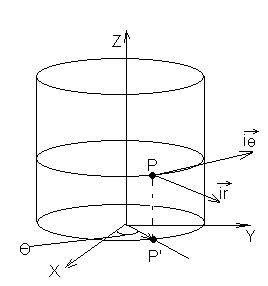 проецируем
точку Р на плоскость XOY
и поведем радиус вектор r
из точки О который является началом как
декартовой системы координат, так и
цилиндрической, в точку Р’ являющейся
проекцией точки Р на плоскость XOY.
Таким образом получим первую координату
цилиндрической системы координат
(радиус r). Угол между OX
и r (Ө). Таким образом мы
получили вторую координату цилиндрической
системы координат. Ось Z
определяет третью координату цилиндрической
системы координат. (r, Ө, Z)
– координаты в цилиндрической системе
координат.
проецируем
точку Р на плоскость XOY
и поведем радиус вектор r
из точки О который является началом как
декартовой системы координат, так и
цилиндрической, в точку Р’ являющейся
проекцией точки Р на плоскость XOY.
Таким образом получим первую координату
цилиндрической системы координат
(радиус r). Угол между OX
и r (Ө). Таким образом мы
получили вторую координату цилиндрической
системы координат. Ось Z
определяет третью координату цилиндрической
системы координат. (r, Ө, Z)
– координаты в цилиндрической системе
координат.
Определим орты данной криволинейной
системы координат. Для этого сделаем
сечение цилиндра плоскостью параллельной
XOY и пересечение данной
плоскости и поверхности цилиндра дает
нам окружность. Проведём из точки Р
единичный вектор
![]() который параллелен r. Этот
орт будет являться первой координатой
r. Проведём единичный
отрезок касающийся полученной окружности
из точки Р в сторону увеличения Ө. -
является второй координатой. Третьим
ортом будет являться отрезок
который параллелен r. Этот
орт будет являться первой координатой
r. Проведём единичный
отрезок касающийся полученной окружности
из точки Р в сторону увеличения Ө. -
является второй координатой. Третьим
ортом будет являться отрезок
![]() - являющийся единичны ортом оси Z.
- являющийся единичны ортом оси Z.
Сферическая система координат:
С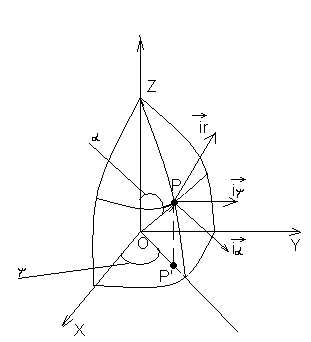 троится
на основе декартовой системы координат.
Предполагаем что некоторая точка
определена в декартовой системе
координат, построим некоторую сферическую
поверхность так что бы искомая точка
лежала на данной поверхности. Проведём
радиус вектор r из точки
О в точку Р и таким образом мы определим
первую координату (r). Угол
отсечённый от OZ между
осью OZ декартовой системы
координат на основании которой строится
сферическая и вектором r
назовем (α) является второй координатой.
Спроецируем точку Р на плоскость XOY
получим Р’. Проведём из точки О в точку
Р’ луч угол между осью OX
и данным лучом отсчитанным от OX
определённый как
троится
на основе декартовой системы координат.
Предполагаем что некоторая точка
определена в декартовой системе
координат, построим некоторую сферическую
поверхность так что бы искомая точка
лежала на данной поверхности. Проведём
радиус вектор r из точки
О в точку Р и таким образом мы определим
первую координату (r). Угол
отсечённый от OZ между
осью OZ декартовой системы
координат на основании которой строится
сферическая и вектором r
назовем (α) является второй координатой.
Спроецируем точку Р на плоскость XOY
получим Р’. Проведём из точки О в точку
Р’ луч угол между осью OX
и данным лучом отсчитанным от OX
определённый как
![]() является третьей координатой сферической
системы координат.
является третьей координатой сферической
системы координат.
Получим орты данной ортогональной
криволинейной системы координат. Для
этого выполним сечение данной сферической
поверхности плоскостью проходящей
через точку Р и осьOZ.
Пресечение данной плоскости и поверхности
сферы даст нам окружность. Из точки Р
отложим единичный вектор
![]() сонаправленный с r. Это
орт будет первой координатой сферической
системы координат. Из точки Р отложим
единичный вектор касающийся полученной
окружности и направленный в сторону
увеличения α – второй орт. Для получения
третьего орта сделаем сечение плоскостью
параллельной XOY и проходящей
через точку Р. Пересечение данной
плоскости со сферой даст нам окружность.
Отложим единичный вектор касающийся
данной окружности и направим в сторону
увеличения
сонаправленный с r. Это
орт будет первой координатой сферической
системы координат. Из точки Р отложим
единичный вектор касающийся полученной
окружности и направленный в сторону
увеличения α – второй орт. Для получения
третьего орта сделаем сечение плоскостью
параллельной XOY и проходящей
через точку Р. Пересечение данной
плоскости со сферой даст нам окружность.
Отложим единичный вектор касающийся
данной окружности и направим в сторону
увеличения
![]() .
.
