Переходные процессы при замыкании и размыкании lr цепи

П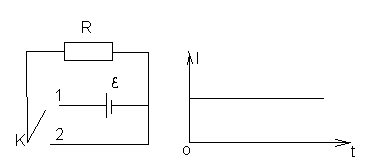ри отсутствии индуктивности в данной цепи зависимость тока от времени будет выглядеть как показано на рисунке. Это говорит о том что при переводе ключа К из положения 2 в положение 1 источник ЭДС мгновенно подключается к электрической цепи. Введём в данную цепь индуктивность величиной L. Подключим последовательно R соленоид который концентрирует МП созданное током в области пространства охваченной поверхностью соленоида и рассмотрим процессы происходящие в данной цепи при переводе ключа К из положения 2 в положение 1.

В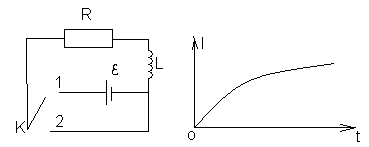 этом случае для замкнутого контура: можно записать второе правило Кирхгофа.

- ЭДС самоиндукции которое возникает в данном контуре в момент изменения тока. В момент перевода ключа из положения 2 в положение 1.

Введём новую переменную

Тогда

Получили дифференциальное уравнение первого порядка которое удобно решить методом разложения переменных

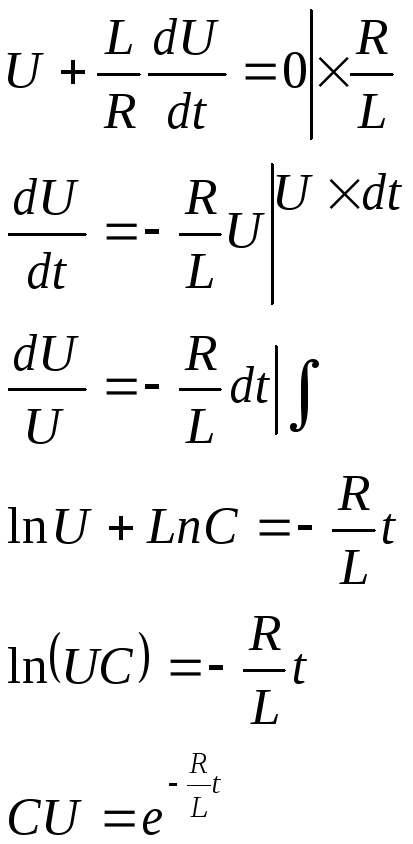
Для нахождения С накладываем начальные условия. В момент времени t=0, I=0

Получаем:

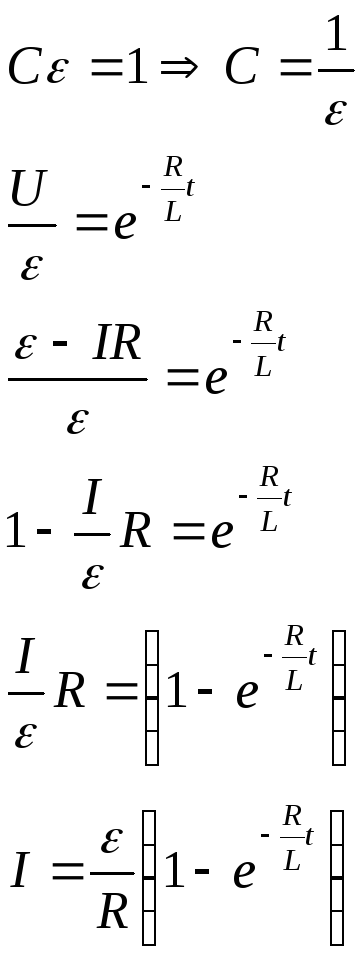
Таким образом из полученного выражения следует что при наличии индуктивности благодаря возникновению экстра токов самоиндукции цепи в момент времени её включения возрастание тока до установившегося значения будет происходить медленнее чем при отсутствии индуктивности.

Процессы при отключении rl цепи

П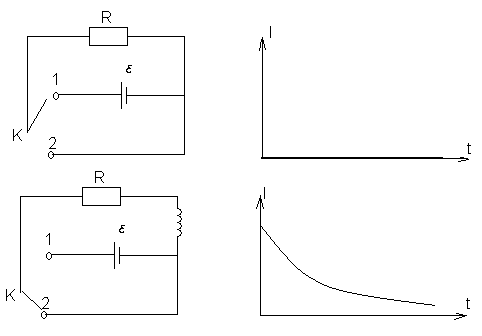ереключатель переводим из положения 1 в положение 2. При переводе ключа второе правило Кирхгофа записывается

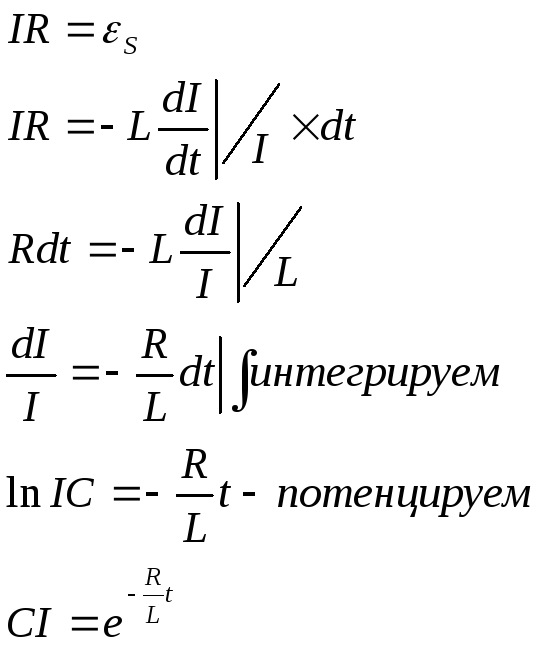
Накладываем начальные условия t=0, I=

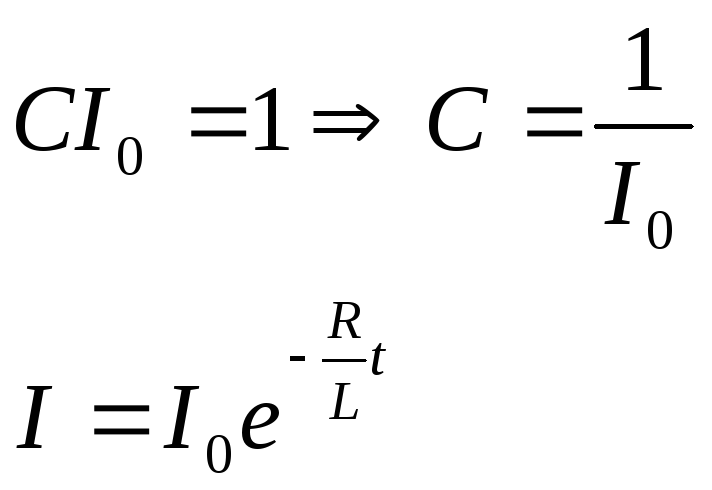
Таким образом благодаря явлению самоиндукции в реальных электрических цепях в процессе включения и отключения процесс нарастания и убывания электрических характеристик проходит медленнее нежели без учёта процесса самоиндукции.

Энергия электрического и магнитного полей.

Общая формула для вычисления энергии электрического поля.

- объём той области пространства в которой необходимо определить поле; - элементарный объём.

С учётом взаимосвязи

А так же учитывая взаимосвязь между напряжённостью и потенциалом

выведем выражение для энергии электрического поля в котором бы фигурировала связь между данной энергией, электрическими характеристиками, а также теми зарядами которые данное поле создает с учётом введенных обозначений для и

Воспользуемся следующим соотношением векторного анализа

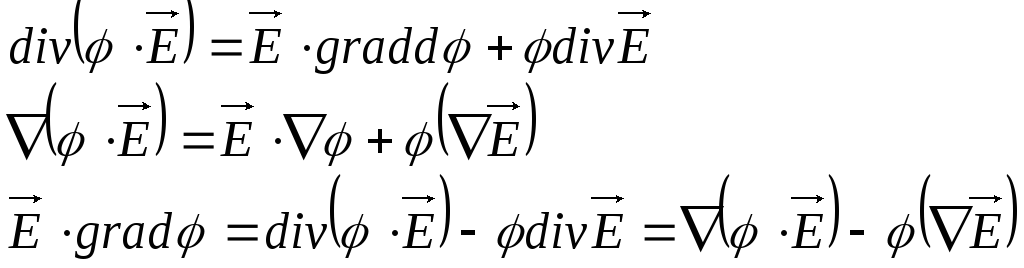
С учётом введённых обозначений

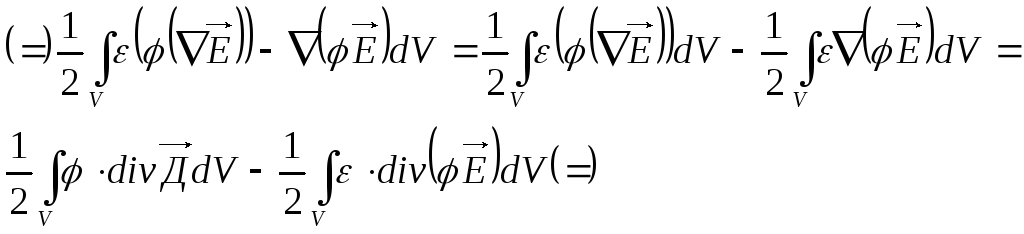
Учитывая теорему Остроградского Гаусса

- замкнутая поверхность охватывающая объём V.

Применяя уравнение обобщающее закон кулона

- объёмная плотность заряда поля индукция которого .

Учитывая что напряженность ЭСП прямо пропорционально

, а потенциал

- расстояние от некоторой точки заряда заряженного с объёмной плотностью . Можно утверждать что порядок малости второго слагаемого значительно больше порядка малости первого слагаемого. Отсюда вторым слагаемым можно пренебречь.

Энергия электрического поля

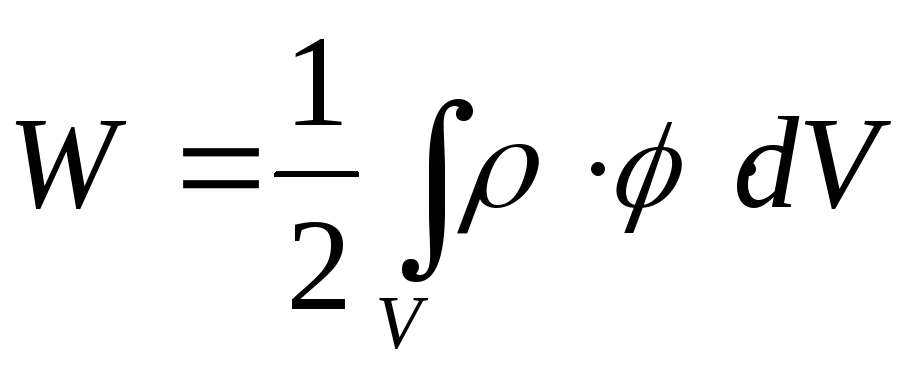
В том случае если заряд будет распределён с некоторой плотностью (по поверхности S), то выражение для электрического поля вырождается в следующее:

Если поле создается некоторым семейством уединённых проводников, то исходя из полученных выражений:

- итый заряд итого проводника из семейства n проводников.

- потенциал ЭСП созданного всеми зарядами в точке расположения заряда i кроме самого итого заряда.

Исходя из общего выражения для энергии и представленного выше выражения для ёмкости уединённого проводника. Можно выразить энергию уединённого проводника через ёмкость данного проводника.

И исходя из данного выражения можно получить выражение для энергии заряженного конденсатора ёмкостью С.

- разность потенциала на обкладках конденсатора

- заряд на обкладках конденсатора.