Метод решения прямой задачи электростатики

Все задачи электростатики прямую и обратную можно решать тремя методами. Среди методов решения прямой задачи электростатики можно выделить три наиболее часто используемых метода.

1) Метод используемый на принципе суперпозиции.

2) Метод основанный на теореме Гаусса.

3) Метод интегрирования уравнения Пуассона.

Граничные условия на границе раздела двух диэлектриков Определение объёмной плотности свободного заряда.

Предполагаем что имеется две среды одна имеет диэлектрическую проницаемость вторая и граница раздела этих сред является поверхность (плоскость) на которой находится заряд распределённый с поверхностной плотностью . Определим как будет соотноситься нормальная составляющая вектора индукции ЭП по отношению к данной границе и как данные составляющие вектора будут связаны с поверхностной плотность . Для этого выделим замкнутую поверхность (цилиндрическую поверхность) так что бы часть этой поверхности находилась в оной среде, а другая часть в другой среде.

И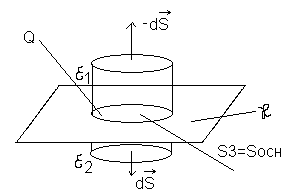 определяем поток вектора электрической индукции через данную замкнутую поверхность.

В соответствием с уравнением Гаусса поток вектора электрической индукции через замкнутую поверхность S равен суммарному свободному заряду находящемуся в нутрии данной замкнутой поверхности.

и - значение векторов индукции ЭП в первой и второй среде соответственно.

Внутри данной замкнутой поверхности другого заряда нет кроме как заряда распределённого по поверхности . Устремим боковую поверхность цилиндра к нулю в этом случае поток через боковую поверхность равен нулю.

Знак минус во втором слагаемом фигурирует потому что нормаль к поверхности основания () составляет с вектором тупой угол в то время как в первой области нормаль к поверхности основания и вектор образуют острый угол.

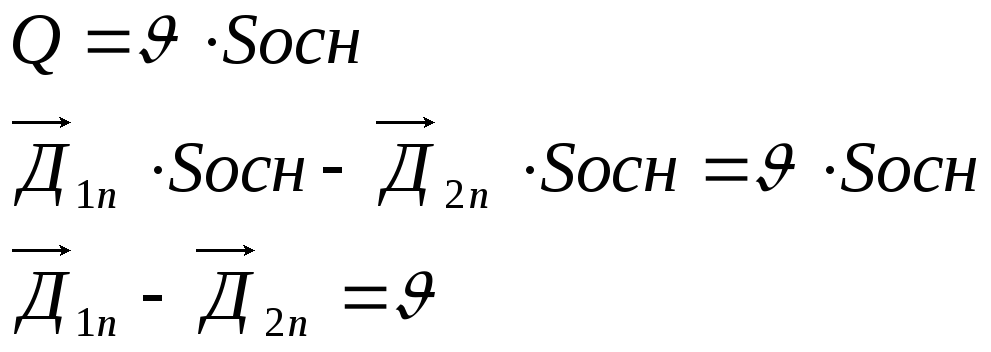
Из данного условия следует что на границе раздела двух сред нормальная составляющая вектора электрической индукции претерпевают разрыв равный поверхностной плотности поверхностного заряда распределённого на границе раздела двух сред. В том случае если на границе раздела двух сред отсутствует распределение свободного заряда с поверхностной плотностью (например на границе раздела двух диэлектриков) то нормальная составляющая вектора индукции разрыва не претерпевают и граничные условия 1 вырождаются в следующие граничные условия .

Найдём соотношение между тангенциальной составляющей векторов напряжённости ЭП на границе радела двух сред. Для этого рассмотрим ситуацию когда две среды с диэлектрическими проницаемостями и разделены некоторой поверхностью (плоскостью). Выберем замкнутый контур на границе раздела двух сред так что бы часть контура находилась в первой области, а другая часть контура во второй области. Так как поле является электростатическим то справедливо:

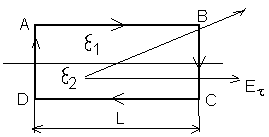
Устремив к нулю высоту данного контура, то есть длину отрезков DA и BC к нулю, получаем:

Знак минус во втором слагаемом фигурирует потому, что направление обхода контура (направление вектора ) образует с тангенциальной составляющей напряжённости ЭП во второй среде 180 градусов в то время как в первой среде 0 градусов.

Таким образом тангенциальная составляющая вектора напряжённости ЭП на границе раздела двух сред не претерпевает разрыва.