
- •Основные понятия и формулы
- •I. Векторная алгебра
- •Линейные операции над векторами
- •Линейная зависимость векторов. Геометрические критерии линейной зависимости
- •Базис и координаты
- •Ортонормированный базис. Декартова прямоугольная система координат
- •II. Аналитическая геометрия в пространстве Плоскость в пространстве
- •Прямая в пространстве
- •Прямая и плоскость в пространстве
- •III. Аналитическая геометрия на плоскости Прямая на плоскости
- •Кривые второго порядка
- •Парабола
- •Преобразования координат
- •IV. Поверхности второго порядка
- •620002, Екатеринбург, ул. Мира, 19
Парабола

Парабола
- геометрическое
место точек
![]() ,
равноудалённых от заданной точки
F(p/2,0)
(фокус)
и от данной прямой (директрисы).
,
равноудалённых от заданной точки
F(p/2,0)
(фокус)
и от данной прямой (директрисы).
![]() .
.
![]() ,
,
![]() -
каноническое
уравнение параболы
с вершиной
в начале координат,
-
каноническое
уравнение параболы
с вершиной
в начале координат,
точка
О
- вершина;
ox
- ось параболы; точка F(р/2,0)
- фокус;
![]() - уравнение
директрисы;
- уравнение
директрисы;
![]() -
эксцентриситет;
p
- фокальный
параметр
(расстояние от фокуса до директрисы или
половина хорды, проходящей через фокус
перпендикулярно оси ox).
-
эксцентриситет;
p
- фокальный
параметр
(расстояние от фокуса до директрисы или
половина хорды, проходящей через фокус
перпендикулярно оси ox).
![]() -
каноническое
уравнение
параболы с вершиной в точке (x0,y0);
-
каноническое
уравнение
параболы с вершиной в точке (x0,y0);
![]() -
уравнение параболы в полярных координатах,
связанных с фокусом;
-
уравнение параболы в полярных координатах,
связанных с фокусом;
 -
параметрические уравнения параболы.
-
параметрические уравнения параболы.
Уравнения прямых
|
|
- уравнения двух пересекающихся прямых; |
|
|
|
- уравнения двух параллельных прямых; |
|
|
|
- уравнение двух совпадающих с осью ox прямых. |
|
Преобразования координат
Для
приведения кривой
![]() к каноническому виду следует подвергнуть
уравнение преобразованиям:
к каноническому виду следует подвергнуть
уравнение преобразованиям:
 и
и
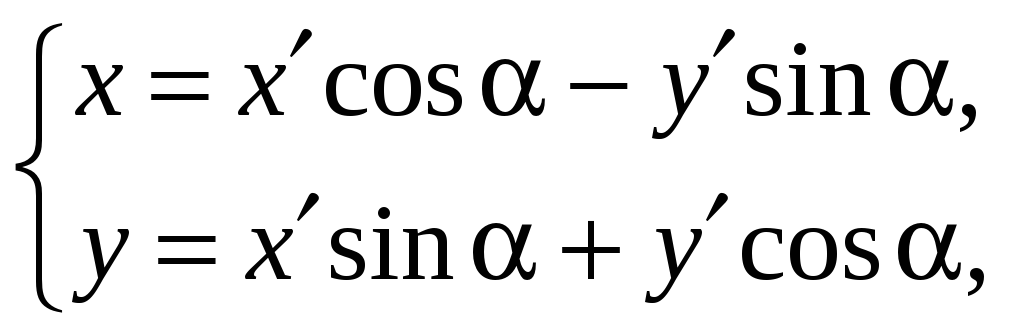
где
 и
и


![]() - уравнение окружности
с центром
- уравнение окружности
с центром
в точке O1(x0,y0) и радиусом R;
 -
уравнения эллипса и гиперболы с
-
уравнения эллипса и гиперболы с
центром симметрии в точке O1(x0,y0);
![]() -
уравнения асимптот гиперболы;
-
уравнения асимптот гиперболы;
![]() -
уравнение параболы с вершиной в точке
O1(x0,y0).
-
уравнение параболы с вершиной в точке
O1(x0,y0).
При
переходе от одной системы прямоугольных
координат к другой мы заменяем уравнение
![]()
линии второго порядка другим уравнением
![]() .
.
При
этом выражения
![]() и
и

остаются равными. Они называются инвариантами (неизменными) уравнения второй степени.
С их помощью различают три типа линий второго порядка.
-
Эллиптический тип, если
 .
.
К нему относятся, кроме действительного эллипса, также мнимый эллипс
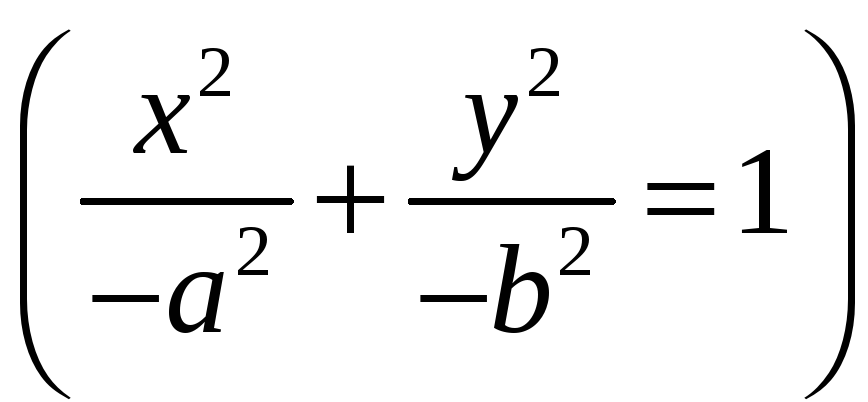
и
пара мнимых прямых, пересекающихся в
действительной точке
 .
.
-
Гиперболический тип, если
 .
.
К
нему относится, кроме гиперболы, пара
действительных пересекающихся прямых
 .
.
-
Параболический тип, если
 .
.
К нему относится, кроме параболы, пара параллельных (действительных или мнимых) прямых (они могут совпадать).
Линии в полярной системе координат
 Полярные координаты
Полярные координаты
![]() ,
,
![]() .
.
Связь полярных координат с декартовыми
M(x,y)
и M(![]() ,):
,):



![]() а=const
>0.
а=const
>0.

![]() ,
а=const >0.
,
а=const >0.
Спирали
А рхимедова
спираль:
рхимедова
спираль:
![]() =а,
=а,![]() .
.
Гиперболическая
спираль:
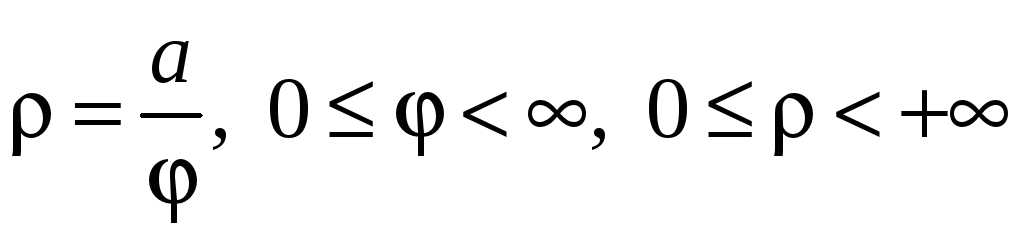 ,
a > 0.
,
a > 0.
Логарифмическая
спираль:
![]() .
.
Розы
Двухлепестковые
розы:
![]() .
.


![]()
![]()
Четырехлепестковые розы a > 0


![]()
![]()
Трёхлепестковые розы:
![]()
![]()


Лемниската Бернулли
![]()

Вершины
кривой находятся в точках
![]()
Площадь каждой петли S=a2.
Кардиоида
В
полярных координатах
![]()

Вершина кардиоиды находится в точке А(2а,0).
Укажем,
что площадь кардиоиды
![]() ,
а длина L=8a.
,
а длина L=8a.
Параметрическое задание линий
Окружность

 - параметрические
уравнения окружности.
- параметрические
уравнения окружности.
Исключим из параметрических уравнений параметр t. Для этого возведём эти уравнения в квадрат и сложим их:
![]() .
.
Циклоида
 где
где
![]() .
.
При
![]() получаем первую арку циклоиды. Укажем,
что длина дуги ОА1О1=8а,
а площадь одной арки S=3
получаем первую арку циклоиды. Укажем,
что длина дуги ОА1О1=8а,
а площадь одной арки S=3![]() a2.
a2.

Астроида


где
![]()
В декартовых координатах уравнение астроиды
x2/3+y2/3=R2/3.
Длина астроиды L=6R, а площадь, ограниченная астроидой S=3R2/8.



