Основные понятия и формулы

I. Векторная алгебра

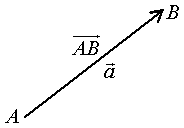В ектор - направленный отрезок.

Векторы коллинеарными, если лежат на одной прямой, либо на параллельных прямых.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

- два вектора равны, если они коллинеарны, имеют одинаковую длину и направление.

Линейные операции над векторами

С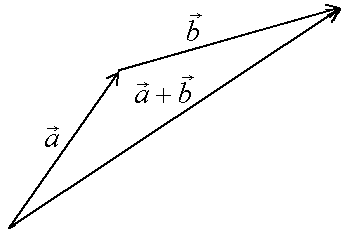 уммой двух векторов и называется вектор, идущий из начала вектора в конец вектора при условии, что начало вектора приложено к концу вектора (правило треугольника).

Свойства:

1 ˚.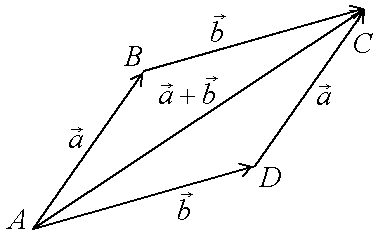

2˚.

3˚.

4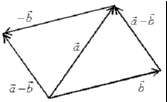˚. Для каждого вектора существует

противоположный ему вектор , такой, что .

Разностью векторов и будет вектор ,

идущий из конца вектора к концу вектора .

Произведение вектора на

в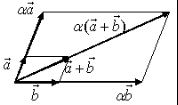ещественное число обладает свойствами:

5˚.

6˚.

7˚.

8˚.

Линейная зависимость векторов. Геометрические критерии линейной зависимости

Линейной комбинацией векторов называют выражение:

,

где - произвольные действительные числа.

Система векторов называется линейно зависимой, если существуют действительные числа , такие, что хотя бы одно из них отлично от нуля, и выполняется равенство:

. (*)

В противном случае, т.е. если линейная комбинация (*) обращается в ноль только при всех , то система векторов называется линейно независимой.

Если векторы линейно зависимы, то любой вектор может быть выражен в виде линейной комбинации остальных.

Геометрические критерии линейной зависимости

Система двух ненулевых векторов линейно зависима тогда, и только тогда, когда векторы коллинеарны.

Система трех векторов линейно зависима тогда и только тогда, когда векторы компланарны.

Базис и координаты

Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке.

Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Базисом на прямой будем называть любой ненулевой вектор этой прямой.

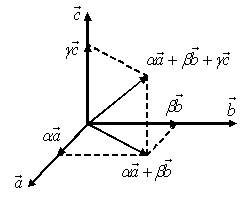Каждый вектор может быть разложен по базису в пространстве и это разложение единственно.

Коэффициенты разложения вектора по базису называются координатами вектора в данном базисе и в каждом базисе определяются однозначно:

.

При сложении двух векторов и их координаты (относительно любого базиса) складываются. При умножении вектора на любое число все его координаты умножаются на это число.

Системой координат в пространстве называют совокупность базиса и некоторой точки, называемой началом координат.

Вектор , идущий из начала координат в точку , называется радиус-вектором точки .

Координатами точки называются координаты вектора .

Таким образом, координаты радиус-вектора и координаты точки совпадают.

Ортонормированный базис. Декартова прямоугольная система координат

Пусть в качестве базиса выбраны три взаимно перпендикулярных вектора с длинами, равными единице.

Обозначения: ,

Т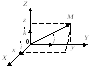 акой базис называется ортонормированным (ОНБ). Векторы называются базисными ортами. Зафиксируем точку О – начало координат и отложим от нее векторы . Полученная система координат называется прямоугольной декартовой. Координаты любого вектора в этом базисе называются декартовыми координатами вектора:

Прямые линии, проведенные через начало координат по направлениям базисных векторов, называются координатными осями: – порождает ; – порождает ; – порождает . Координаты точки М (вектора ) в декартовой системе координат по осям , , называются соответственно абсциссой, ординатой и аппликатой.

Декартовы прямоугольные координаты вектора равны проекциям этого вектора на оси , , соответственно; другими словами,

, , .

Здесь – углы, которые составляет вектор с координатными осями , , соответственно, при этом , , называются направляющими косинусами вектора .

Вектор 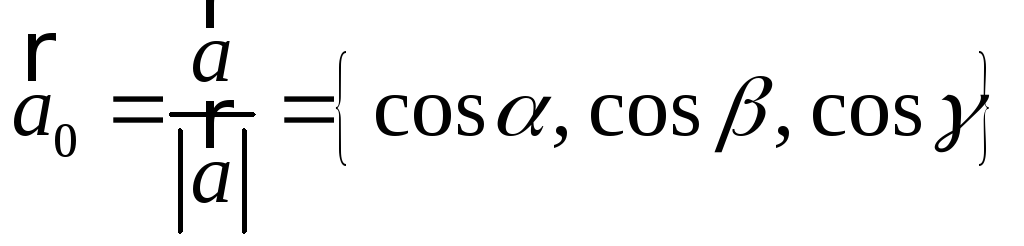представляет собой вектор единичной длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение:

.

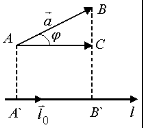
Проекция вектора на ось l равна

, где - орт оси l.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними: .

Если , , то .

Алгебраические и геометрические свойства:

1°. .

2°.

3°. , .

4°. , если , и , если .

5°. ; .

6°. .

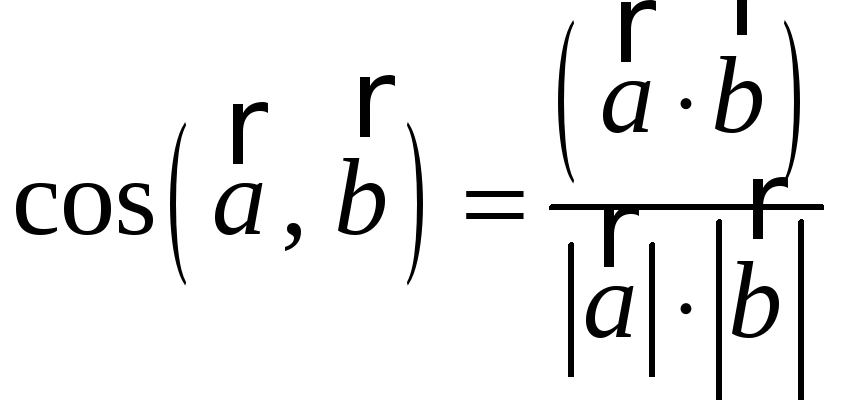
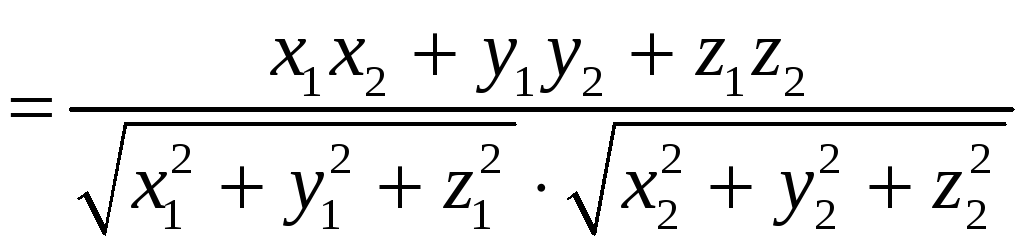7°. =, .

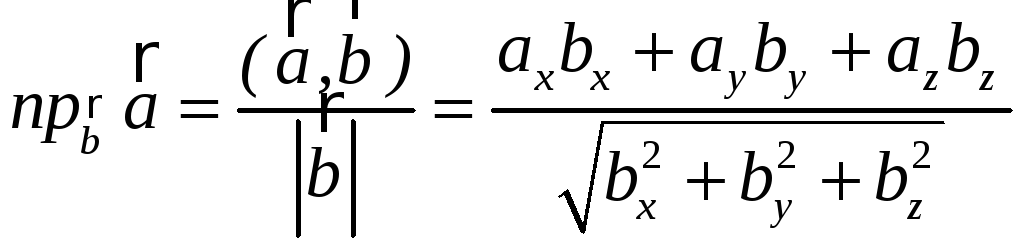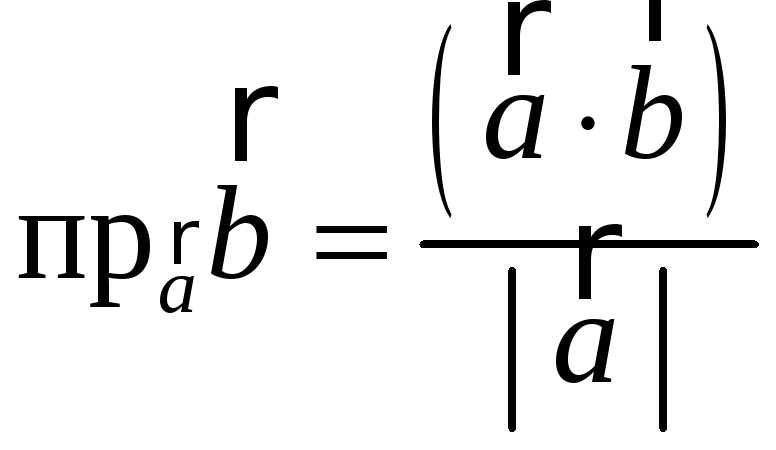8°. : - условие перпендикулярности.

9°. , - длина вектора.

10°. , , – расстояние между двумя точками.

11°. Направляющие косинусы вектора: , , ;

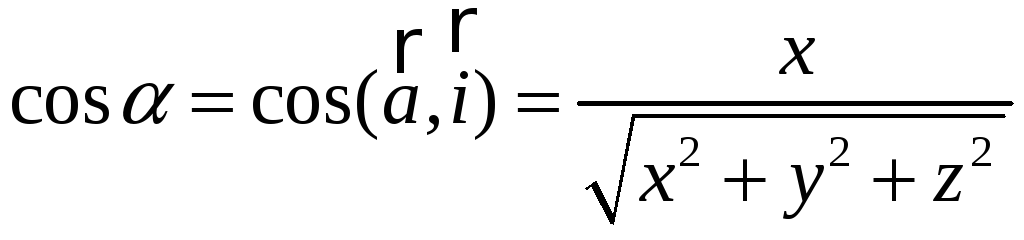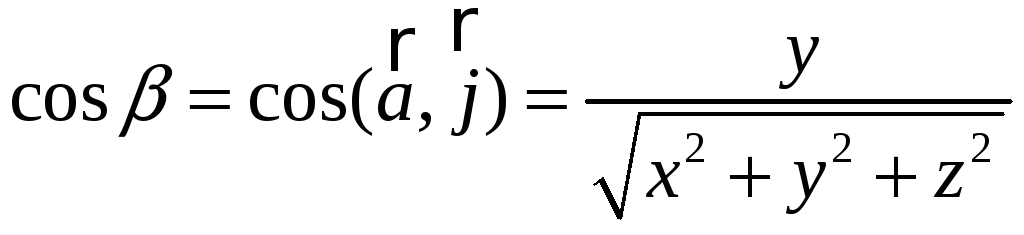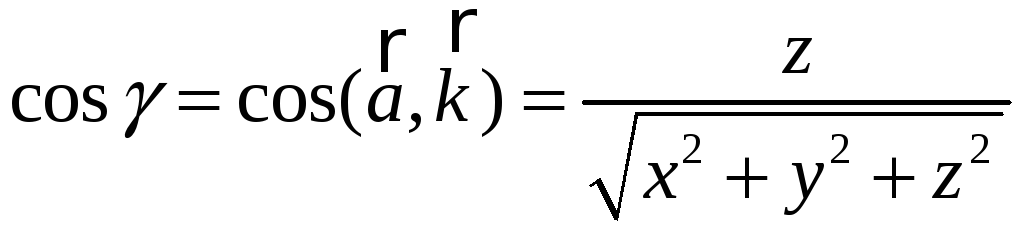cos² α + cos² β + cos² = 1

Упорядоченная тройка некомпланарных векторов , , , приведенных к одному началу, называется правой, если из конца третьего вектора кратчайший поворот первого вектора ко второму виден совершаемым против часовой стрелки. В противном случае тройка называется левой.

правая

левая

При перестановке местами двух соседних векторов ориентация тройки меняется.

Если тройки , , - правые, то , , - левые.

При круговой (циклической) перестановке векторов ориентация тройки не меняется.

Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим трем требованиям:

1). Длина вектора равна произведению длин векторов и на синус угла между ними, т.е..

2). Вектор ортогонален к каждому из векторов и , т.е. перпендикулярен плоскости, в которой лежат векторы и .

3). Вектор направлен так, что тройка является правой.

Алгебраические и геометрические свойства:

1°..

2. .

3. .

4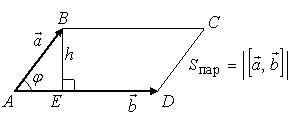. для любого вектора .

5. =

6. коллинеарен .

Если , , ,

.

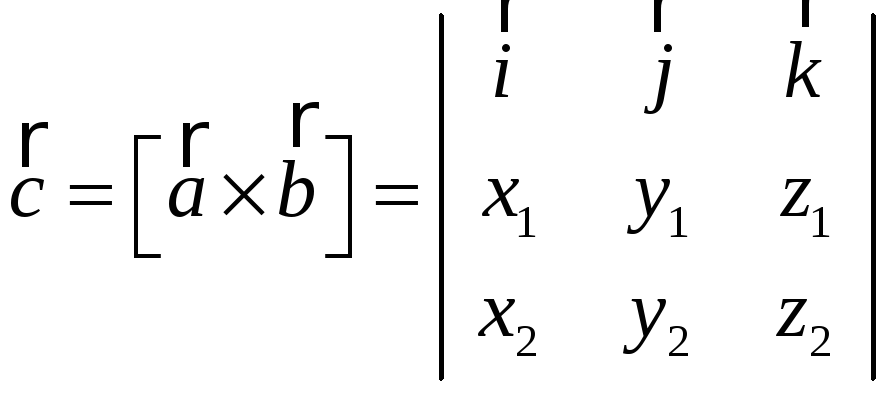Если и коллинеарны, то .

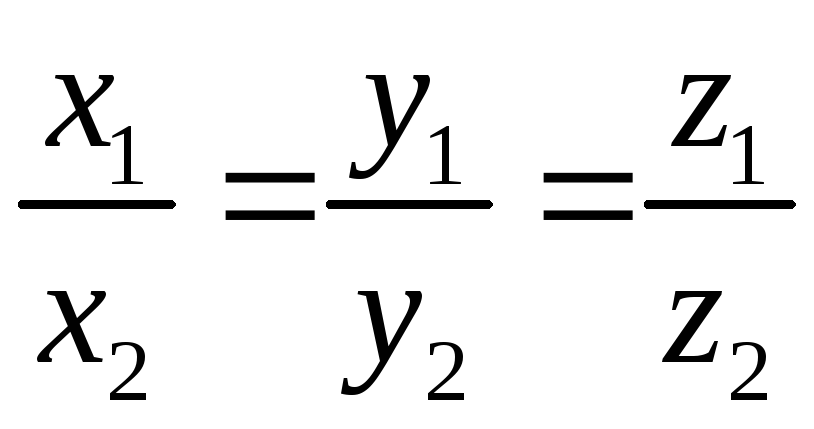Смешанное произведение некомпланарных векторов по абсолютной величине равно объему параллелепипеда, построенного на этих векторах, приведенных к одному началу.

положительно, если тройка , , правая и отрицательно, если она левая.

Е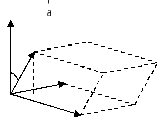сли же векторы , , компланарны, то равно нулю: .

, .

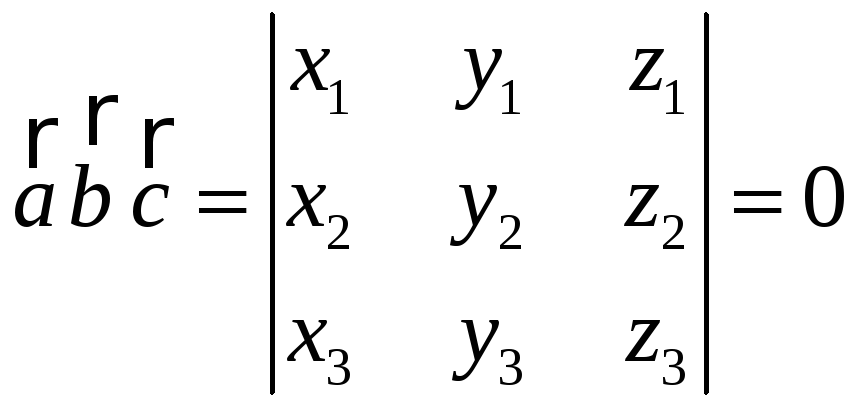смешанное произведение зависит от порядка сомножителей, но не зависит от того, какие сомножители связаны первичным знаком векторного произведения.

Если , , , то .
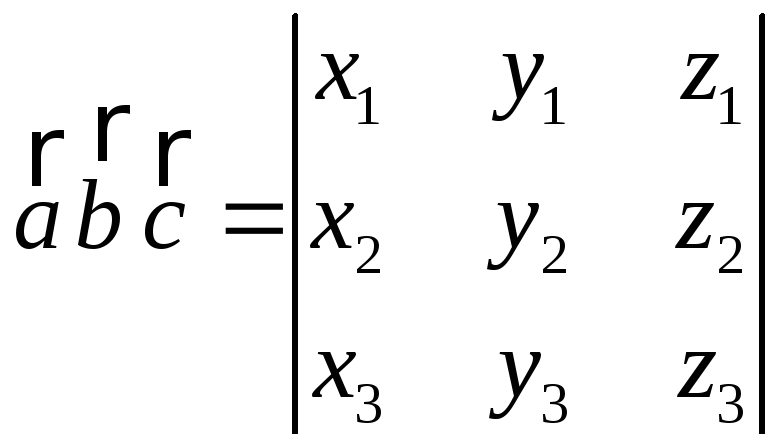