1.5. Релятивистская динамика.

В конце 19 века было показано, что классическая механика не применима к описанию движения тел с очень большими, близкими к скорости света, скоростями. Это позволяет делать теория, созданная А.Эйнштейном.

Специальная теория относительности (СТО) или по другому релятивистская динамика опирается на два постулата:

Первый постулат (принцип относительности): все законы физики имеют одинаковую форму во всех инерциальных системах отсчета (ИСО).

В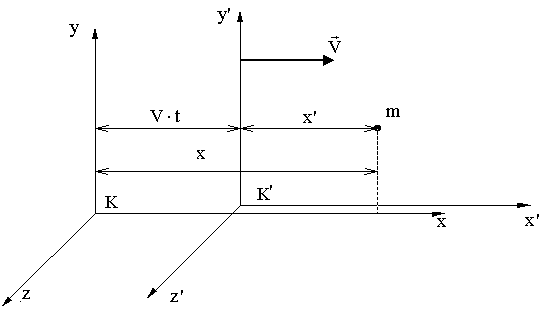торой постулат (постоянство скорости света): свет распространяется в пустом пространстве со скоростью с = 3·10⁸ м/с, не зави­сящей от скорости движения источника или наблюдателя.

Пусть система отсчета K является неподвижной, а система K’ движется относи­тельно нее вдоль оси x со скоростью υ.

Уравнения преобразования координат и времени для т. m при переходе от одной ИСО к другой, полученные Лоренцем, имеют вид:

Следствия из преобразований Лоренца.

1. Сокращение длины. Пусть вдоль оси x’ в движущейся системе отсчета K’ лежит стержень длины ℓ_o (это собственная длина или длина предмета (стержня) в той системе отсчета, в которой он покоится). Тогда ℓ – длина стержня относительно неподвижной системы отсчета K – равна :

Таким образом, движущийся предмет кажется наблюдателю более коротким, чем покоящий­ся. Сокращение происходит только в направле­нии относительного движения и становится за­метным лишь при υ, близкой к скорости света в вакууме с.

2. Замедление времени. ,

где Δt₀ – собственное время, т.е. промежу­ток времени в системе, где часы покоятся, Δt соответствует промежутку времени в системе, относительно которой часы движутся, причем Δt > Δt₀ . Таким образом, движущиеся часы идут медленнее покоящихся.

3. Относительность одновременности. События, одновременные в одной ИСО, оказываются неодновременными по отношению к другой ИСО.

4. Релятивистские формулы преобразо­вания скоростей (закон сложения скоростей) получаются дифференцированием по времени преобразований Лоренца:

;

;

.

Здесь и_х , и_у , u_z , u’_x , u’_y и и'_г — проекции скорости движущейся частицы на оси неподвижной и по­движной систем отсчета, соответственно. Отсюда следует, что скорость света, равная u’_x = с относительно системы отсчета K’, и относительно K будет равна и_х = с.

Физические величины, которые не меняются при переходе от одной инерциальной системы к другой, называются инвариантами теории относительности. К инвариантам, например, относятся скорость света в вакууме, масса и электрический заряд частицы, пространственно-временной интервал .

А. Эйнштейн показал, что закон природы – основное уравнение динамики – будет инвариантен к преобразованиям Лоренца, если импульс тела будет иметь вид: .

Из этой формулы видно, что тело, обладающее массой, не может двигаться со скоростью, большей или равной скорости света с . Из этой же формулы следует, что со скоростью света может двигаться, обладая конечным импульсом, только безмассовая частица (m=0). Это, например, фотон.

Основное уравнение динамики в СТО принимает, т.о., вид:

.

Если сила совершает работу, разгоняя тело от нулевой скорости до некоторой релятивистской скорости , то эта работа целиком идет на создание кинетической энергии, т.е.: . Вычисление интеграла приводит к выражению: .

Если истолковывать как полную энергию тела, то отсюда следует, что когда тело покоит­ся и его кинетическая энергия равна нулю, оно тем не менее обладает энергией т_·с². В соот­ветствии с этим т_·с² называют энергией покоя тела : Е₀ = m·c². Это знаменитая формула Эйнштейна, говорящая о том, что масса тела является не только мерой инертно­сти или мерой гравитационного действия, но и мерой энергосодержания тела. Используя выражения для импульса и энергии тела можно получить еще одно часто используемое выражение для полной энергии тела:

.

Согласно СТО, пространство и время являются относительными, зависят друг от друга, образуя единый 4-х мерный пространственно-временной континуум.

Несколько позже в общей теории относительности А. Эйнштейн показал, что на пространство и время влияет тяготение, а именно, вблизи очень массивных тел пространство искривляется, а время замедляется.