1.3.2. Критерий произведений

Заметим, что критерий произведений (-критерий) не принадлежит к числу произ­водных критериев. Если, однако, рассматривать логарифмы ре­зультатов решения, то он переходит в -критерий и потому может рассматриваться как производный от последнего.

Оценочной функцией на сей раз служит величина

.

В случае двух состояний и и при обозначениях , получаем для линий уровня

. (1.12)

Они представляют собой, таким образом, семейство гипербол (рис. 1.9), прилегающих к лучам конуса предпочтения -критерия. При возрастании значения эти гиперболы переходят в прямую предпочтения -критерия . Оптимальное решение и для -критерия получается в результате перемеще­ния конуса предпочтения вправо – вверх вдоль направляющей до тех пор, пока он в последний раз не заденет поле по­лезности.

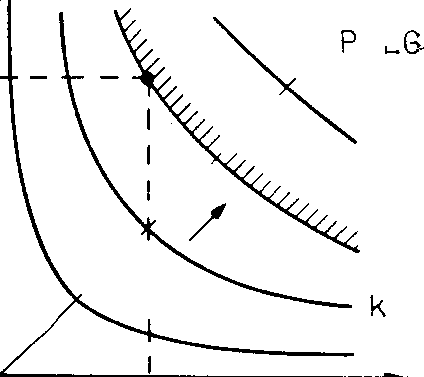
Рис. 1.9. Функции предпочтения -критерия

1.3.3. Критерий Гурвица

В случае -критерия, максимизирующего, согласно

,

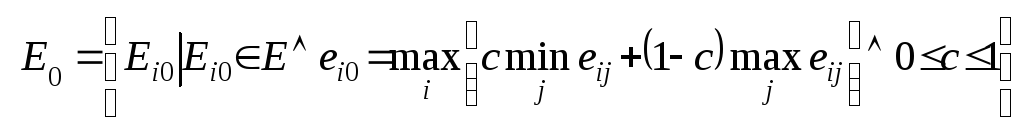где – весовой множитель,

оценочную функцию

, ,

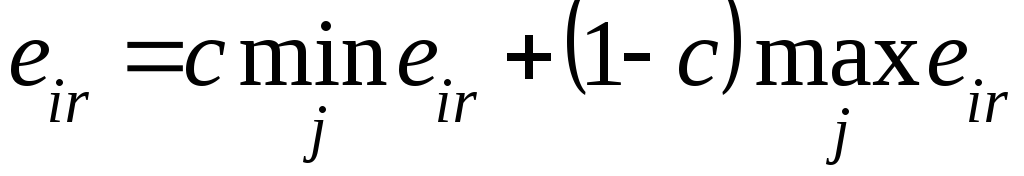в случае двух состояний и и при обозначениях , получаем для семейства линий уровня

, . (1.13)

На рис. 1.10 показаны эти линии уровня для трех значений , , .

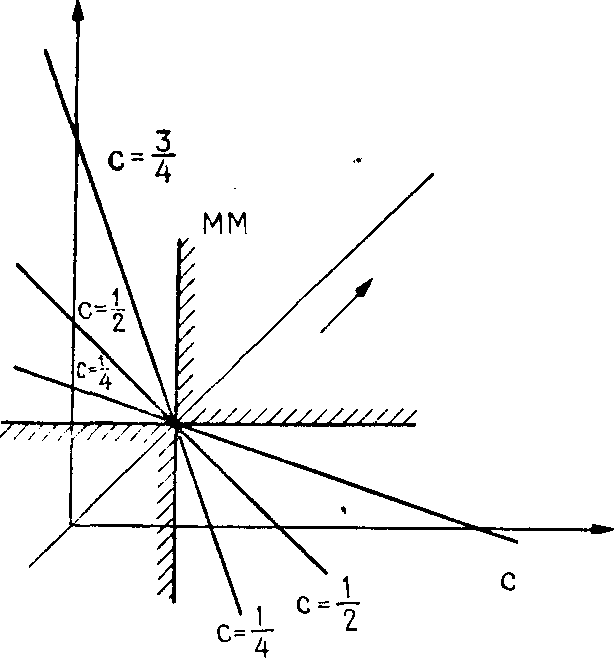
Рис. 1.10. Функции предпочтения -критерия

-критерий представляет собой комбинацию -критерия и критерия азартного игрока . Здесь является весовым множителем: чем ближе к 1 (соответственно, к 0), тем боль­ше влияние -критерия (соответственно, -критерия). При оба критерия равноценны, и в качестве конусов пред­почтения получаются обыкновенные прямые, как в случае нейт­рального -критерия. Оптимальное согласно -критерию решение вновь получается в результате перемещения конуса (для ) или, соответственно, антиконуса (для ) предпочтения вправо – вверх до тех пор, пока он в последний раз не коснется поля полезности.

1.3.4. Критерий Байеса-Лапласа

Графическая интерпретация -критерия не так проста, как в ранее рассмотренных слу­чаях. Это связано в первую очередь с наличием множеств и , ограничивающих выбор вариантов решений. Рис. 1.11 опять-таки для случая двух со­стояний проясняет существо дела для значений допустимого риска , , . Выделим сначала в поле полезности точку и соответствующий конус пред­почтения , определяемый -критерием. Нарисуем за­тем конус предпочтения с образующими, параллель­ными образующим первого конуса, и уровнем, пониженным на величину допустимого риска .

Рис. 1.11. Графический выбор в соответствии с -критерием

Угловая область, на­ходящаяся между этими двумя конусами, содержит – включая границу – величины полезности из множества согласия . С другой стороны, справа и выше прямой , проходящей через точку и параллельной биссектрисе второго и четвер­того координатных углов, расположены все точки поля полез­ности, для которых соответствующие варианты решений при­надлежат выигрышному множеству . Допустимая область состоит тогда из обеих заштрихованных подобластей. Се­мейство линий уровня будет то же, что и для -критерия (разд. 1.2). Направляющая прямая исходит из начала коорди­нат и имеет угловой коэффициент . Семейство пер­пендикулярных ей линий уровня и некоторая точка из заштри­хованной области, обладающая наивысшим согласно -критерию уровнем, определяют оптимальное решение.