7.1.2. Реализация целей

Если необходимо принять решение, имея в виду К конкури­рующих целей, то на основе оценки К получают матрицу реше­ний , , где – полезность при состоянии исходных данных и варианте решения применительно к цели . Каждая из (двумерных) матриц определяется по известным оценочным функциям. В результате для каждой мат­рицы при определенном получают матрицу решений . При этом часть вариантов решения выделяется для опти­мизации. Уже это часто позволяет прояснить ситуацию с выбо­ром решения. В частности, множество

может состоять из единственного варианта, и в этом случае за­дача решается однозначно. Если множество вариантов решения существенно ограничено, то оптимальный вариант может быть выбран субъективно.

Если не удается прийти к определенному решению уже на этой стадии, то следует сначала пронормировать реализацию цели, например, следующим образом:

, (7.1)

где – -e значение цели варианта ;

– степень реализа­ции -й цели -гo варианта.

Во многих встречающихся на практике случаях не удается определить и (или) . Тогда приходится идти по другому пути нормирования. Если не удается определить , то можно пронормировать следующим

образом:

, (7.2)

а если нельзя определить то, соответственно,

. (7.3)

Если же неизвестны оба экстремальных значения, то удовлет­ворительный результат дает нормировка относительно прини­маемой за базовую величину

. (7.4)

При нормировке по формуле (7.4) предполагается, что су­ществует приемлемое решение, которое может рассматриваться как достаточное и использоваться в качестве базового.

При субъективно устанавливаемых весах целей удается получаемую двумерную матрицу преобразовать в один вектор. Компоненты этого вектора определяются аддитивным сочетанием взвешенных степеней реализации:

. (7.5)

Вектор теперь можно вновь интерпретировать как матри­цу решений и соответствующим образом оценивать.

Здесь нужно особо упомянуть доминирующий на практике случай, когда цели связаны дизъюнктивно (то есть по принципу ИЛИ). Таким образом, связаны цели, которые можно сравнить друг с другом, так что меньшая степень реализации одной цели может быть скомпенсирована лучшим исполнением другой. На­оборот, для конъюнктивно (то есть по принципу И) связанных це­лей характерно положение, когда невыполнение одной частной цели ведет к тому, что не достигается итоговая цель.

Часто из-за низкой точности интуитивной оценки веса целей дальнейшее рассмотрение теряет смысл.

Конъюнктивная связь целей приводит, например, в частном случае к соотношению

. (7.6)

При смешанной связи получают, например,

.

Примером нелинейного взвешивания является

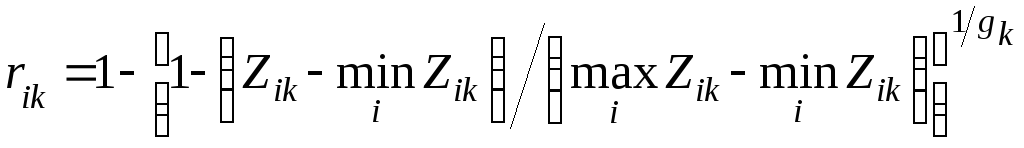. (7.7)

Однако прежде чем предпринимать усилия в этом направлении, следует здраво оценить, не ведут ли к цели более рациональ­ным путем другие теоретические предпосылки.