6.5. Виды рисков

Установки и приборы подвергаются опасности при возрас­тании нагрузки. Если при этом будет превзойден предел (на­пример, прочности), произойдет выход из строя. Риск здесь со­ответствует частному случаю, описываемому уравнением (6.5), при условиях:

а) если последствия выхода из строя нельзя выразить в эко­номических категориях;

б) если экономические соображения играют подчиненную роль и перевешивают не поддающиеся оценке факторы;

в) если экономические последствия также важны, но не поддаются количественной оценке;

г) если последствия столь велики, что без особых рассуж­дений нужно минимизировать возможность выхода из строя.

Технический риск характеризуется, таким образом, вероят­ностью превышения предела . Если и – случайные пере­менные, причем характеризует нагрузку, а – несущую спо­собность, то для технического риска справедливо соотношение

, (6.15)

что в случае существования плотностей вероятности и со­ответственно для нагрузки и несущей способности и при сто­хастической независимости и дает

.

Если, кроме того, можно описать временной ход нагрузки и несущей способности плотностями вероятности и соответственно, получим

. (6.16)

Если существует множество, например, независимых друг от друга величин нагрузки , и, соответственно, несущей способ­ности , , то справедливо соотношение .

Вместе с тем значения плотностей вероятности для несущей способности и нагрузки определить трудно. В то время как в строительстве легче определить несущую способность, чем на­грузку, в электротехнике ситуация обычно обратная. При из­вестных условиях можно облегчить задачу, предполагая нали­чие одноточечного распределения, исходя при этом из наиболее неблагоприятного случая и моделируя решаемую задачу путем соответствующего преобразования приведенных выше формул для случая принятия решения в условиях неопределенности.

В следующих рассуждениях мы исходим из того, что послед­ствия при конкретных нагрузке и несущей способности у мож­но описать функцией . Прежде всего, казалось бы, важно рассмотреть критический случай , то есть случай, когда несущая способность ниже уровня нагрузки. Можно было бы выразить это условием для и однозначно оценить критический случай простым утверждением, что при этом . Однако реальные данные из практики по­казывают, что иногда первые признаки разрушения появляются еще до достижения нагрузкой несущей способности, и наоборот, в других случаях, при нагрузке, превышающей несущую спо­собность, конструкция еще работает, так что ограничение функ­ции всего двумя значениями – 0 и 1 – может оказаться слишком грубым описанием. Определим теперь эко­номический риск при стохастической независимости нагруз­ки и несущей способности и данных плотностях вероятно­сти и ожидаемых случайных величин соотноше­нием

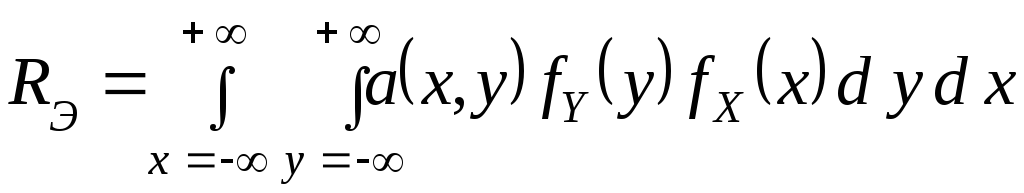. (6.17)

Для определенного данного значения нагрузки условное математическое ожидание риска равно

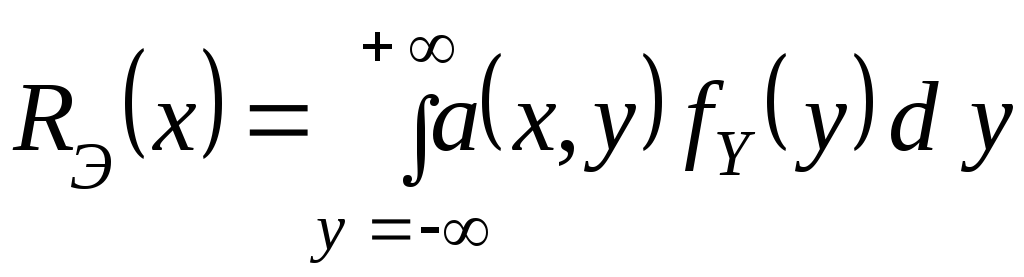. (6.18)

Если нагрузка и несущая способность описываются дискретны­ми распределениями, а именно

	Значения	Вероятности

а вредные последствия характеризуются величинами , , , то вместо (6.17)

получим

. (6.19)

Введенные математические ожидания риска можно рассмат­ривать как элементы матрицы решений. Расчет матрицы осу­ществляют тогда в соответствии с ранее изученными методами.

Если можно в случае угрозы людям задать функцию риска, то справедливы соотношения, аналогичные формулам (6.17) – (6.19), приведенным для технико-экономического риска. В про­тивном случае здесь, как и в случае технического риска, нужно применить в качестве меры риска вероятность угрозы. Допол­нительно следует, однако, рассмотреть еще ряд связей.

Угроза при эксплуатации технических средств определяется двумя категориями влияний – представляющими угрозу собы­тиями и попаданием в опасную зону.

Обычно представляющие угрозу события и попадание в опасную зону – явления случайные. Анализ во временной об­ласти дает (в предположении равномерных распределений) следующие выражения для вероятности наступления представ­ляющего угрозу события:

. (6.20)

и для вероятности попадания в опасную зону:

. (6.21)

Таким образом, вероятности выражаются как отношения интервалов времени. Здесь приняты следующие обозначения:

– суммарная продолжительность представляющего угрозу события; – продолжительность пребывания в опасной зоне;

– весь рассматриваемый интервал времени.

Если представляющее угрозу событие и пребывание в опасной зоне независимы, то для вероятности их совместной реализации справедлива формула

. (6.22)

Эта формула говорит, что при данных значениях и в смысле, определяемом формулами (6.20) и (6.21), следует считаться с вероятностью совпадения опасностей, то есть одновременного наступления представляющего угрозу события и попадания в опасную зону в рассматриваемый отрезок вре­мени. Отсюда, однако, не следует, с какой вероятностью нужно ожидать реализации, по меньшей мере, одной угрозы. Поэтому при использования величины как вероятности угрозы возможны серьезные ошибки в интерпретации рассматриваемых ситуаций.

Коль скоро мы исходили из того, что уже в очень малом промежутке времени совпадение будет представлять опасность, имеет смысл положить в основу дальнейшего рассмотрения ве­роятность угрозы появления по крайней мере одного совпа­дения в рассматриваемом интервале времени . Для определе­ния разобьем рассматриваемый отрезок времени в одном случае на равновеликих интервалов продолжительностью , а в другом – на равновеликих интервалов продолжительно­стью .

Рис.6.6. Регулярное появление (то есть одинаковое по продолжительности и разделенное равными промежутками времени) А (Н=3) и случайные неблаго­приятные события Е (h=2)

Интервал сравнительно короткий и соответствует на­ступлению представляющего угрозу события, а интервал существенно длиннее и соответствует попаданию в опасную зону. Сообразно условиям эксплуатации техники характерной вели­чиной для может, например, быть 1 секунда, тогда как для речь идет о часах. Соотношение между и обозначим и будем характеризовать величинами и, соответственно, общее число угрожающих событий или попаданий в опасную зону. Путем комбинаторных рассмотрений нетрудно получить для вероятности несовпадения выражения

, (6.23)

и отсюда, благодаря равенству , вероятность угрозы

. (6.24)

Практический интерес представляет то положение, что фор­мулы (6.23) и (6.24) остаются справедливыми и тогда, когда интервалы попадания в опасную зону не случайны и, например, эквидистантны на интервале , и только события в смысле их появления остаются случайными, хотя и подчиняются равно­мерному распределению по . Пример такой ситуации показан на рис. 6.6, причем, как видно, имеет место и одно совпадение.

В заключение заметим, что формулы (6.23) и (6.24), в от­личие от (6.22), несмотря на остающиеся постоянными вели­чины и , зависят от и , то есть когда и , как и , варьируют таким образом, чтобы и каждый раз оставались постоянными, то величина вероятности, определяемая формулой (6.22), не меняется, а величины вероятно­стей, определяемые формулами (6.23) и (6.24), – меняются.

На рис. 6.7 схематично показаны две ситуации с одинако­выми значениями и , но во втором случае наступает вдвое больше отдельных событий, каждое из которых вдвое короче по продолжительности.

Если для двух сравниваемых ситуаций справедливы соот­ношения и , то отсюда следует и ( – натуральное число), и справедливо равенство .

А	H=1, N=6 h=2, v=3, n=18
Е

А Е

H’=1, N’=6 h’=4=2h, l’=1/2 l v’=6=2v, n’=36=2π

Рис.6.7. События с одинаковой общей и различной индивидуальной продолжительностью

Для вероятности несовпадения по (6.23) нетрудно получить неравенство:

.

Это означает, что при неограниченном уменьшении единич­ного интервала для неблагоприятного события вероятность угрозы стремится к единице.

Известно, что рассчитать вероятность угрозы можно по формуле

. (6.25)

Заметим, что такой способ предложил ученый Бауэр.

Вероятности и получаются из (6.20) и (6.21), а и означают число попаданий в опасную зону и неблагоприят­ных событий соответственно за рассматриваемое время. При этом если речь идет о случайных величинах, нужно использо­вать оценки для их средних значений. В области, представляю­щей практический интерес, формулы (6.24) и (6.25) хорошо согласуются между собой: кроме того, в частности, при , формула (6.25) удобнее для расчетов, чем (6.24). Для очень малых вероятностей и удовлетворительный резуль­тат дает формула

. (6.26)

График рис. 6.8 позволяет определить максимальную ошибку, которую дает формула (6.26) в наиболее неблагоприятном случае , . До значений вероятности угрозы менее 10^–2 ошибка не превышает 1%. Для определения в более широ­кой области используют номограмму рис. 6.7

Из точки на оси абсцисс, соответствующей вероятности угрозы, восставляют перпендикуляр до пересечения с прямой, соответствующей числу попаданий в опасную зону, и для точки пересечения берут отсчет по правой вспомогательной шкале на оси ординат. Аналогичным образом для известных величин вероятности попадания в опасную зону и числа угрожающих событий получают на вспомогательной шкале.

Рис. 6.8. Максимальная ошибка приближения по формуле (6.26)

отсчет II. Сложение обоих отрезков на ординате III дает свя­занную с неблагоприятными событиями вероятность угрозы, считываемую по левой шкале

Дополнительно нужно указать, что формулы (6.25) и (6.26) представляют в большей или меньшей степени грубые прибли­жения к (6.24). Так, например, случай , приводит согласно (6.25) к парадоксальному результату . Также для из (6.25) следует соотношение

,

тогда как опасность возможна только в случае .