5.3. Ошибки решения

5.3.1. Количественный анализ ошибок

На практике часто встречается случай, когда функция по­лезности , где характеризует состояния исходных дан­ных, а – варианты решения, известна не точно, а с некоторой неопределенностью или ошибкой , так что принимаю­щему решение приходится иметь дело не с самой функцией по­лезности , а с отягощенной ошибкой ее формой .

Возникает вопрос, какая погрешность возникает, когда оп­тимизацию приходится проводить, исходя из функции вместо функции . Можно, правда, предполо­жить, что достаточно малая погрешность мало повли­яет на максимальную эффективность и доминирующие вариан­ты решения, но нельзя ожидать, что это общее предположение будет справедливо в одинаковой мере для всех критериев выбо­ра и ошибок . Если, однако, величина посто­янна и не зависит от и , то есть , что на практике является весьма нередким частным случаем, то при использо­вании различных ранее обсуждавшихся критериев получаются такие же оптимальные варианты решения, как и для задачи, не отягощенной погрешностями оценок. Мы покажем это на важ­ных примерах критерия Байеса-Лапласа, а также минимакс­ного и гибкого критериев. Будем в общем случае исходить из того, что переменные и могут изменяться как непрерывно, так и дискретно, и независимо от природы переменных пронор­мируем диапазон их изменения в пределы [0,1]. Сформулиро­ванное выше высказывание верно, когда при использовании критерия оптимальное значение величины оценочной функ­ции , которое мы хотим получить, не зависящая от и ошибка и соответствующая ей погрешность подчиняются уравнению

,

то есть . Для минимаксного критерия с оценочной функцией и непосредственно получаем

, т.с.

В случае критерия Байеса-Лапласа вместо прежней дискретной формы

используем для непрерывно меняющихся переменных с произвольной функцией распределения непрерывную форму:

.

Отсюда следует

,

и поскольку , то .

Наконец, для гибкого критерия, исходя из выражения

с ,

Получим

,

и, следовательно, снова .

Таким образом, подтверждается положение, что постоянная, то есть не зависящая от внешних состояний и вариантов решения ошибка в определении функции полезности для рассмотренных нами случаев ведет к постоянной и такой же по величине погрешности оценочной функции, однако сами оптимальные ва­рианты решений остаются теми же, что и в случае отсутствия ошибки.

О зависимости значения оценочной функции от погрешно­сти функции полезности и о воздействии этой погрешности на выбор оптимального варианта нужно еще сказать следующее. Мы принимаем, что значение оценочной функции для крите­рия соответствует состоянию исходных данных и опти­мальному варианту решения , то есть справедливо равенство , и можно упростить символику обозначений, записывая функциональную зависимость символом . 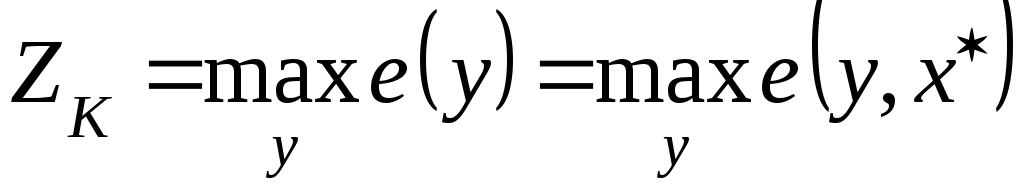При этом функция предполагается дифферен­цируемой, так что существует производная , и поскольку , то . Если теперь вместо функции полезности мы располагаем отягощенной ошиб­кой функцией и максимальное значение по­следней соответствует варианту решения , то для ошибки в случае

справедлива оценка

.

При этом аргумент во второй производной имеет про­межуточное значение между и . Коль скоро для предпо­лагается так называемый гладкий максимум и первая произ­водная в будет меняться лишь незначительно, то и значе­ние второй производной в окрестности будет мало и даже при больших отклонениях оптимального варианта реше­ния от ошибка будет определяться главным образом ошибкой функции полезности .