3.3. Адаптивный критерий Кофлера-Менга с использованием кусочно-линейной информации

В работе Е. Кофлера и Г. Менга показывают преимуще­ства предлагаемого ими адаптивного критерия, который ориен­тирован на уровень информации, имеющейся у лица, принимаю­щего решение. Недостающая информация, образующая мно­жество , задается в виде имеющихся в распоряжении апри­орных вероятностных распределений внешних состояний. При этом принимается предположение о том, что пространство этих состояний может быть разложено на непересекающиеся подмножества : , для .

Лицо, принимающее решение, знает, что внешние состояния из подмножества встречаются с вероятностью :

, , .

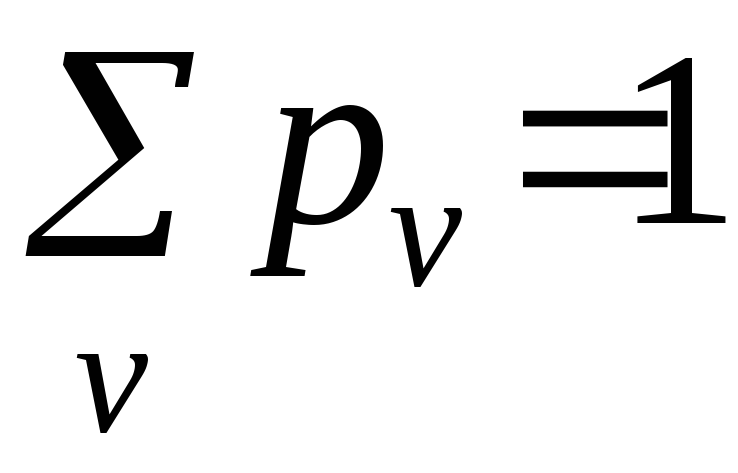В случае появления состояния при выборе варианта ре­шения результат представляется в виде величины . Кофлер и Менг определяют оценочную функцию адаптивного критерия следующим

образом:

, (3.11)

где – множество вариантов решения. Таким образом, реше­ние является оптимальным, если выполняется равенство

.

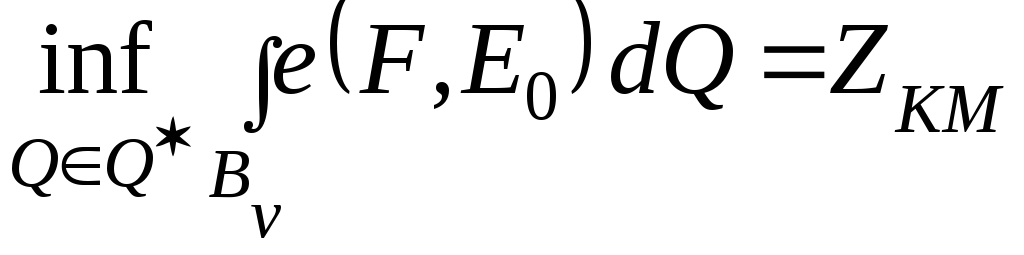Критерий, определяемый выражением (3.11), может быть оха­рактеризован как «бернуллизация» минимаксного критерия, по­скольку выбор оптимального варианта по Бернулли состоит, по существу, в том, что максимизируется математическое ожида­ние результата. Область применения критерия может быть рас­ширена, поскольку момент времени принятия решения не зада­ется, и лицо, принимающее решение, располагает возможностью выбрать благоприятное для себя время.

Множество априорных вероятностных распределений обра­зует для конечного числа внешних состояний (пусть – их число) конечномерный симплекс . Частичная информация состоит тогда в знании некоторого (не вырождающегося до од­ного распределения) собственного подсимплекса . При этом говорят о кусочно-линейной информации (КЛИ), если указан­ная часть симплекса образует выпуклое многомерное подпро­странство. Кусочно-линейная информация обладает различны­ми важными свойствами, например, в вероятностном подпро­странстве этой информации существует реальная точка экстре­мума, координаты которой составляют матрицу. Кроме того, на основании априорного вероятностного распределения или априорного задания частотного распределения значений пара­метра по интервалам можно получить апостериорное вероят­ностное распределение или, соответственно, апостериорное час­тотное распределение параметра по интервалам, но, конечно, также кусочно-линейного типа.

Если для симплекса распределения внешних состояний априорное распределение кусочной информации представлено в форме части этого симплекса , то отношение

, ,

где и – объемы, соответственно, подпростран­ства и пространства , представляет собой относитель­ную энтропию.

Чувствительностью ситуации по отношению к за­данному изменению информации называется приращение результата , вызванное изменением .

Наряду с одношаговыми существуют также и многошаговые процессы принятия решения. Формирование процесса адапта­ции выполняется с использованием известной в стохастической динамической оптимизации -стратегии. Специально для усвоения метода ав­торы вводят понятие стохастической линейной программы , , .

Цель Кофлера и Менга состояла в количественном согласо­вании информации, характеризующей конкретную ситуацию, с возможными вариантами решения, что совпадает с постанов­кой задачи в разд. 3.1, хотя критерии выбора различаются.

Метод КЛИ не содержит никаких конкретных указаний, как и откуда получать оговоренную выше кусочно-линейную ин­формацию при наличии объективного описания существующей ситуации. Таким образом, степень объективности КЛИ оценить нельзя, что, конечно, серьезно ограничивает возможности широ­кого применения адаптивного критерия.

Рассматривая вопросы, связанные с оценкой риска, и интерпретируя границы доверительных интервалов вероятностных оценок рас­пределения параметров или полученные для них наиболее не­благоприятные распределения параметров как экстремальные точки и, соответственно, экстремаль­ное распределение в смысле, получим одинаковые резуль­таты решения как с использованием гибкого критерия (3.1), так и с использованием адаптивного критерия. Однако вычис­лительные затраты, связанные с применением адаптивного кри­терия, существенно выше. Экстремальные распределения или точки необходимо получать из систем неравенств, которые со­ставляются на основании всей возможной информации о рас­пределении внешних состояний. Риск, сопутствующий принятию решения по адаптивному критерию, не оценивается, тогда как использование гибкого критерия (3.1) предусматривает оценку и контроль величины допустимого риска. Гибкий крите­рий принятия решения (3.1) характеризуется большой степенью общности с классическими критериями – при соответствующей оценке риска выбор варианта решения может выполняться, кроме выше описанных случаев, по -критерию, а использование эмпирико-прогностического доверительного фактора способствует эффекту стабилизации выбора варианта решения при повторных случаях принятия решения в аналогич­ной ситуации. Таким образом, область применения данного критерия значительно шире по сравнению с классическими и содержит элементы моделирования процесса с целью улучше­ния качества решения.

Вопросы для самопроверки по разделу 3

1. Дать краткую характеристику свойств гибкого критерия выбора решения.

2. Изложить основы применения гибкого критерия выбора решения.

3. Привести особенности применения гибкого критерия выбора решения.

4. Дать понятие адаптивного критерия Кофлера-Менга.

5. Привести особенности использования адаптивного критерия Кофлера-Менга.