Лабораторная работа № 2 моделирование на эвм процесса внезапного металлического трехфазного короткого замыкания

Цель работы. Исследовать процесс внезапного металлического трехфазного

короткого замыкания в активно-индуктивной цепи.

Пояснения к работе.

Процесс трехфазного металлического короткого замыкания рассмотрим в простейшей электрической системе (рис. 2.1) [2,5]. Пусть питание системы осуществ­ляется от источника бесконечной мощности с сопротивлением равным нулю.

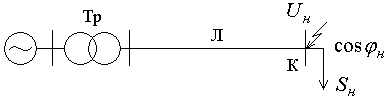
Рис.2.1 – Исследуемая электрическая система

На рис. 2.2 приведена схема замещения рассматриваемой системы. Па­раметры схемы замещения для разных вариантов, приведенные к номинальному напряжению в месте КЗ –Uн, све­дены в табл. 2.1.

Рис.2.2– Схема замещения исследуемой электрической системы

Ток, протекавший в этой цепи перед коротким замыканием, называ­ется предшествующим. Например, предшествующий ток фазы А можно определить по формуле

. (2.1)

Здесь – амплитуда фазного напряжения;

– амплитуда фазного тока;

– угловая частота сети;

– полное сопротивление системы;

– активное сопротивление системы;

– реактивное сопротивление системы;

– угол сдвига между током и напряжением.

Пусть в точке K (рис. 2.2) на шинах произошло трехфазное короткое замыкание. Как правило, в месте короткого замыкания возникает электрическая дуга, сопротивление ко­торой необходимо учесть в сопротивлении цепи короткого замыка­ния. Рассмотрим металлическое короткое замыкание, при этом сопро­тивление дуги [2]. Дифференциальное уравнение переходного про­цесса, возникающего при коротком замыкании, например, для фазы А можно записать в следующем виде:

(2.2)

Решением этого уравнения является выражение 2

, (2.3)

где , - периодическая и апериодическая составляющие тока;

– амплитуда периодической составляющей тока;

– постоянная времени апериодической составляющей

тока;

– полное сопротивлений цепи oт точки питания до точки

замыкания (цепи КЗ);

– активное сопротивление цепи КЗ;

– реактивное сопротивление цепи КЗ;

– угол сдвига между током и напряжением в цепи КЗ;

– начальное значение апериодической составлявшей тока;

– индуктивность цепи КЗ:

– фаза напряжения при времени .

По первому закону коммутации (ток в индуктивной цепи скачком изме­ниться не может [1]) запишем

или .

Отсюда находим начальное значение апериодической составляющей тока

. (2.4)

На рис. 2.3 показаны зависимость и ее составляющие.

Максимальное значение полного тока короткого замыкания (рис. 2.3) называют ударным током , а отношение ударного тока к амплитуде периодической составляющей – ударным коэффициентом . Величины и необходимо знать для правильного выбора ап­паратуры, они зависят от параметров цепи и предшествующего режима. Рассмотрим это влияние.

Сначала проанализируем случай, когда отсутствует предшествующий ток (короткое замыкание линии работавшей на холостом ходу). Из уравнения (2.4) находим начальное значение апериодической состав­ляющей тока

. (2.5)

Величина i₀ зависит от фазы включения и может изменяться от максимального значения до нуля. Наибольшее начальное значение апериодической составляющей имеет место при угле . Отсюда

(2.6)

Однако, наибольшее значение апериодической составляющей еще не пред-определяет того, что именно в этот момент будет максимум мгновенного значения тока. Ведь полный ток в цепи КЗ является функцией двух независимых переменных: времени и фазы включения . Можно показать, что максимум полного тока имеет место при [2] (ес­ли в момент возникновения короткого замыкания напряжение источника проходит через нуль). Принимая во внимание, что высоковольтные цепи электрических систем представляют собой цепи с преобладающей индуктивностью, для которых [3], можно считать, что условие наибольшего начального значения апериодической составляющей (2.6) и условие возникновения максимума мгновенного значения полного тока практически совпадают. Ударный ток короткого замыкания в этом случае возникает примерно через полпериода частоты 50 Гц, т.е. через . Ударный ток

(2.7)

где - ударный коэффициент (при ).

При () ударный коэффициент , в реальных схе­мах . Из выражения (2.5) также следует, что при  = _к апериодическая составляющая вообще не возникнет и сразу наступает установившийся режим, т.е. .

Таким образом, коэффициент может изменяться от 1 до 2 и зависит от (рис. 2.4). Если угол , то возникнет на первой полуволне, а при – на второй. В лабораторной работе при необходимо построить зависимость .

А теперь учтем предшествующий ток. Если , то первое и вто­рое слагаемые в формуле (2.4) имеют разные знаки, поэтому предшест­вующий ток при любых уменьшает , а следовательно, и полный ток (рис. 2.4).

В общем случае . Поэтому при изменении от до есть участки, где знаки слагаемых в формуле (2.4) противоположны (следовательно, предшествующий ток уменьшает полный ток) и одинако­вы (предшествующий ток увеличивает полный ток). В лабораторной ра­боте при необходимо построить зависимость (рис. 2.4).

Все вышеприведенные формулы и рассуждения справедливы и для фаз В и С. Необходимо только учесть, что фазы их включения сдвинуты на угол .

Рис. 2.З– Кривая и ее составляющие: