Поверхностная плотность заряда

Но известно (для изотропной среды):

Следовательно:

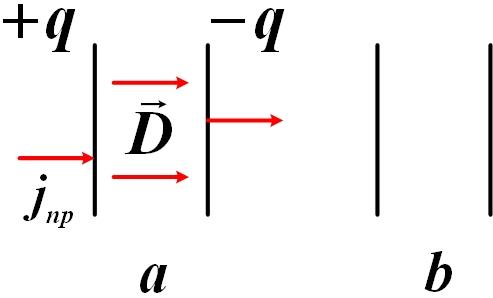
Наиболее общим свойством каждого тока является способность создавать магнитное поле. Магнитное поле токов проводника было открыто Эрстедом в 1820 году. Величина его определяется законом Био – Саварра – Лапласа (1820 год).

В 1901 году А.А. Эйхенвальд показал, что конвекционные токи, образованные движением в пространстве заряженных тел и поляризованных диэлектриков, создают такое же магнитное поле, как и токи проводимости

В 1911 году Иоффе А.Ф. обнаружил магнитное поле электронов, движущихся в вакууме, так же эквивалентное току проводимости.

Из всех физических свойств, присущих току Максвелл приписал току смещения лишь одно – способность создавать магнитное поле, аналогично магнитному полю токов проводника:

Если в проводнике переменный ток, то внутри проводника есть и ток проводимости, и ток смещения, и магнитное поле определяется полным током:

Тогда:

II.

Закон полного тока.

Ток смещения есть там, где меняется со временем электрическое поле. В диэлектриках ток смещения состоит из двух различных слагаемых:

- ток смещения (плотность тока); - плотность тока поляризации, обусловленная движением связанных зарядов.

Ток поляризации возбуждает магнитное поле – эти токи не отличаются по природе о токов проводимости.

Принципиально новое – - не связано ни с каким движением зарядов, а только с изменением электрического поля - - возбуждает магнитное поле.

Даже в вакууме всякое изменение электрического поля возбуждает в окружающем пространстве магнитное поле.

- открытие тока смещения – к открытию электромагнитного поля.

Ваша специальность включает исследование свойств материалов в электрических и магнитных полях.

Сравним величины токов проводимости и токов смещения для различных материалов:

Пусть синусоидальное поле:

(Отношение амплитуд):

В вакууме:

Таким образом, при обычных частотах в металлах токи смещения малы по сравнению с токами проводимости. Они соизмеримы при Гц – это несколько ангстрем – рентгеновские лучи.

В полупроводниках токи проводимости и токи смещения одного порядка при Гц (дециметровый диапазон).

В диэлектриках токи смещения больше токов проводимости уже при низких частотах (переменный ток).

Дополнив основные факты из области электромагнетизма установлением магнитных действий токов смещения, Максвелл смог написать систему фундаментальных уравнений электродинамики:

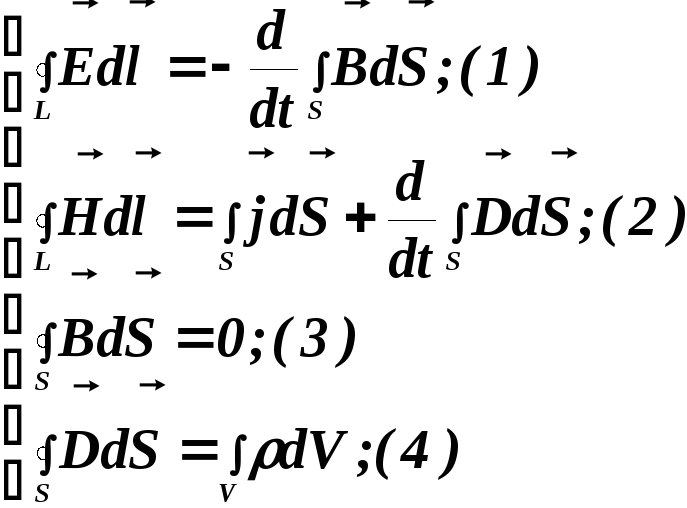
Материальные уравнения:

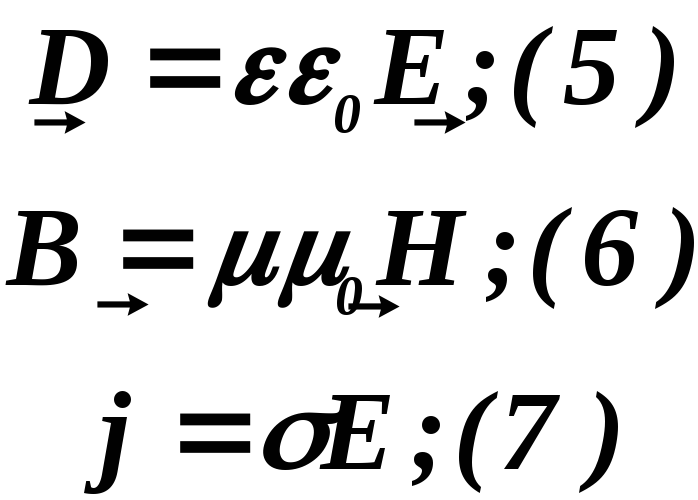
8. Уравнение Максвелла в дифференциальной форме

Уравнения Максвелла применимы к поверхности любой величины и поэтому входящие в них величины относятся к разным точкам поля. Так, например, в уравнении:

- напряженность магнитного поля в точках контура , Ограничивающего поверхность S, в то время как поток вектора зависит от значения в точках самой поверхности.

Можно, однако, преобразовать эти уравнения в такую форму, чтобы все величины относились к одной и той же точке поля. Для этого уравнения Максвелла нужно применить к поверхности бесконечно малой величины.

Согласно теореме Стокса:

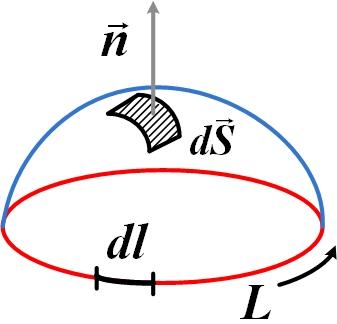
Тогда первое уравнение:

(I)

Справа интеграл зависит только от времени, → при фиксированном контуре правая часть никак не меняется при любых изменениях .

Символ ;

Второе уравнение:

По теореме Стокса:

(II)

Расхождения электрической и магнитной индукции

Третье и четвертое уравнения Максвелла:

Переход от интегральной к дифференциальной форме согласно теореме Остроградского – Гаусса:

(3)

(4)

Схема уравнений Максвелла в дифференциальной форме:

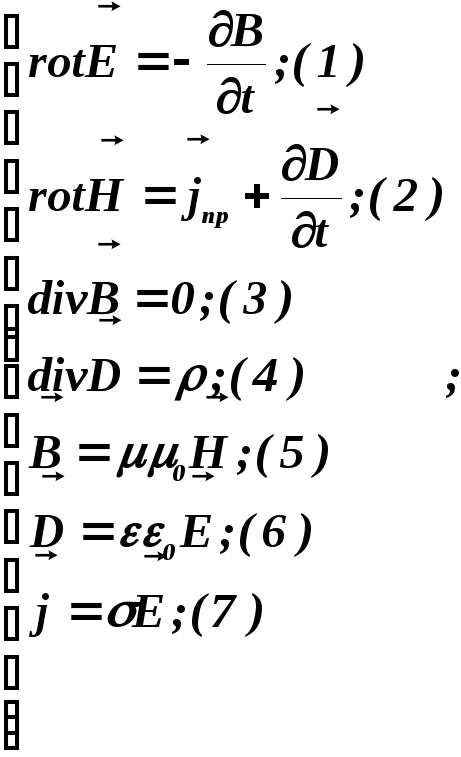
(σ - удельная проводимость)