6. Построить графики вероятностей с помощью мастера диаграмм.

7. Выполнить анализ полученных результатов.

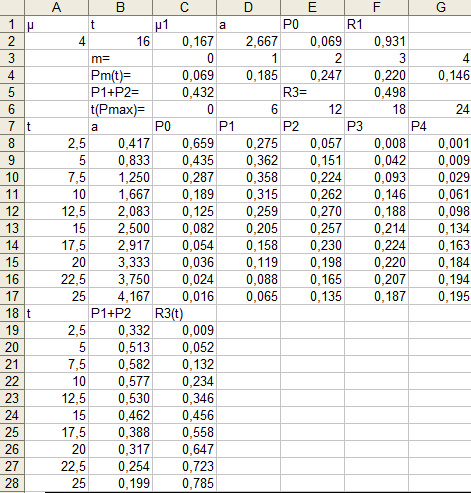
Расчетные формулы представлены в таблице 1, результаты расчета на рис. 1-3.

Таблица 1. Расчетные формулы

	A	B	C	D	E	F	G
1		t		a
2	4	16	=a2/24	=c2*b2	=EXP(-d2)	=1-e2
3			0	1	2	3	4
4		P(t)=	=*
5			=c3/$c$2
6			=d4+e4		=1-(c4+c6)
7	t	a
8	5	=$c$2*a8	=*
9	10
…
18
19
20	5	=d8+e8	=1-(c8+b20)
21	10
22
…
30

Примечания. 1. В ячейку С4 записана формула =$d$2^c3*EXP(-$d$2)/ФАКТР(c3), в ячейку С8 - =$b8^c$3*EXP(-$b8)/ФАКТР(c$3).

2. Стрелки и означают копирование в эти ячейки.

Размещение информации на рабочем листе ЭТ

Иллюстрация 4-го свойства простейшего потока вызовов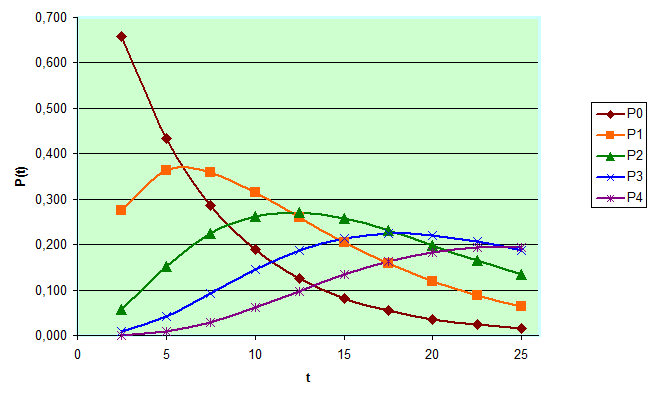

График вероятностей поступления одного или более двух вызовов

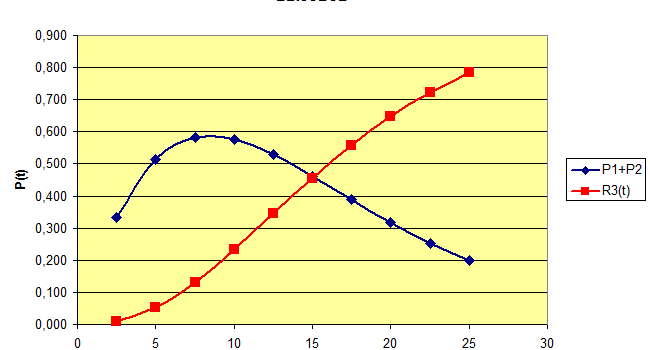
Анализ результатов. Полученные результаты позволяют сделать некоторые предварительные выводы. Вероятность того, что в течение 16 часов поступит :

• хотя бы один вызов, равна R1=0.931

• один или два вызова, равна P1+P2=0.432

• более двух вызовов, равна R3=0.498

Следовательно, через каждые 16 часов можно ожидать один-два вызова на выполнение аварийных работ. Более чем два вызова в среднем будут поступать в 50 случаях из ста. На основе этого можно предположить численный состав аварийной службы в данном случае, т.е. при плотности потока 4 вызова в сутки

Задачи 3 и 4. Расчет выполнялся для µ =0.2; t=28 ч Т_об=20 мин.

Таблица 1. Размещение информации

	A	B	C	D	E	F	G	H	I
1		t	a
2	0,2	28	=a2*b2
3	m=	0	1	2	3	4	5	6
4	P(t)=	=*
5								R7	=1-i4
6
7	Тоб,мин	Тоб, ч	a
8	20	=a8/60	=a2*b8
9	m	2	3	4	5	6	7	8
10	P(Тоб)=	=*

Примечание. В ячейки В4 и В10 соответственно записаны формулы: =$c$2^b3*EXP(-$c$2)/ФАКТР(b3); =$c$8^b9*EXP(-$c$8)/ФАКТР(b9).

Таблица 3. Результаты расчета

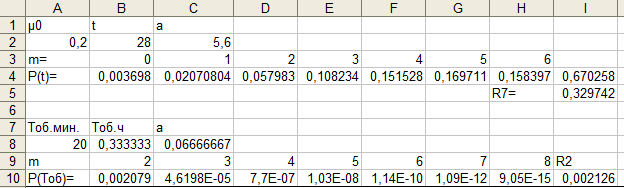
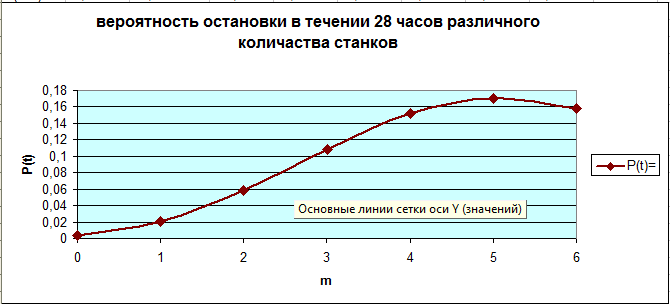
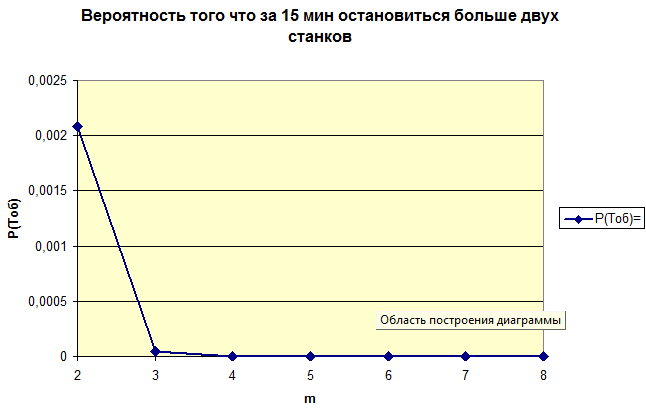
Анализ результатов расчета. Наиболее вероятно, что после 28 часов работы потребуют обслуживание 5 станков. Более 6 станков могут потребовать обслуживание в 33 случаях из ста, так как =0,329742 Вероятность того, что за 20 мин обслуживания остановится не меньше двух станков, равна ∑P_i(Т_об)=0,002126 т.е. вероятность эта мала. Следовательно, можно надеяться, что за это время остановится один станок или ни одного.

9