§11. Элементы математической статистики. Основные понятия

Математическая статистика – это раздел теории вероятностей. Занимается она сбором и обработкой опытных данных, т.е. прикладными задачами теории вероятностей.

Как уже отмечалось в §2, частота появления случайного события стремится к вероятности этого события, если число испытаний неограниченно растет. Поэтому на практике, когда вероятность неизвестна, ее заменяют на частоту, получаемую экспериментально. Говорят, что частота р^* является оценкой вероятности р, т.е. ее приближенным значением.

Основной задачей математической статистики является оценка закона распределения случайной величины или числовых характеристик, если в законе распределения нет необходимости.

Пусть при неоднократном измерении некоторой случайной (или неслучайной) величины мы получили серию из n результатов (x₁, x₂, …, x_n). В силу неизбежных случайных ошибок измерения не все результаты измерений одной и той же величины будут совпадать друг с другом.

Очевидно, любое измерение x_i можно считать оценкой измеряемой величины, если она неслучайная, или оценкой ее математического ожидания, если это случайная величина . Однако, интуитивно ясно, что среднее арифметическое n измерений

(1)

будет более точной оценкой математического ожидания m_ случайной величины Среднее арифметическое обычно и берут в качестве оценки математического ожидания, т.е. m_.

Оценкой начальных моментов k-го порядка _k служат соответствующие статистические моменты , т.е.

_k. (2)

Оценкой центральных моментов _k служат соответствующие статистические центральные моменты , т.е. _k. (3)

Если известно математическое ожидание m_то в качестве оценки _kлучше взять величину

. (4)

Определение. Статистической функцией распределения F^*(x) случайной величины  называют частоту события (<x), т.е.

F^*(x)=Р^*(<x), (5)

где Р^*(<x) - частота события (<x).

Чтобы найти значение F^*(x), нужно подсчитать число испытаний (измерений), в которых величина  принимает значение меньшее х, и разделить это число на общее число испытаний n.

Аналитически статистическую функцию распределения можно записать так

F^*(x) , (5)

где (х) – функция Хевисайда.

Очевидно, и для дискретной, и для непрерывной случайной величины  функция F^*(x) будет ступенчатой, разрывной в точках x_i. Все свойства функции распределения F(x) справедливы и для статистической функции распределения F^*(x). Поскольку частота события (<x) стремится к вероятности этого события, то естественно в качестве оценки функции F(x) взять функцию F^*(x).

Повторим серию независимых измерений случайной величины  и, в силу случайных ошибок, вместо прежней серии измерений (x₁, x₂, …, x_n) получим новую (x₁’, x₂’, …, x_n’). Отсюда ясно, что серию измерений (x₁, x₂, …, x_n)=х можно рассматривать как случайный вектор, а его координаты x_i как случайные величины, имеющие тот же закон распределения, что и измеряемая случайная величина . Ясно также, что все статистические моменты являются величинами случайными. При оценке числовых характеристик мы заменяем точные значения на случайные величины. Указать предельную погрешность, которую мы совершаем при этом, мы не можем, т.к. она не имеет смысла. Однако методы статистики, которые мы рассмотрим позже, позволяют найти вероятность такой погрешности.

Случайный вектор х=(x₁, x₂, …, x_n) называют выборкой из генеральной совокупности. Под генеральной совокупностью понимают всю бесконечную мыслимую совокупность измерений. Приведем другой пример. Пусть необходимо узнать средний бюджет жителей Таганрога. Для этого придется опросить всех жителей города. Они и представляют собой генеральную совокупность. Т.к. опросить всех жителей города задача трудоемкая и дорогостоящая, то делают случайную выборку, т.е. опрашивают только некоторую часть жителей города, но результат опроса распространяется на всех. Ясно, что результаты эти будут случайными.

Обработать выборку можно различными способами. Если измерения x_i упорядочить по величине, расположив в порядке неубывания, то полученную выборку называют вариационным рядом. Разность R=x_max-x_min называется размахом выборки. Если в вариационном ряде оставить только различные измерения, но указать их частоту повторения, то получим статистический ряд.

Если объем выборки велик, то весь интервал выборки разбивают на несколько разрядов. Подсчитывают число измерений, попавших в каждый разряд, вычисляют частоту каждого разряда, т.е. отношение числа измерений в разряде к числу всех измерений выборки, и все это сводят в таблицу, которая называется группированным статистическим рядом.

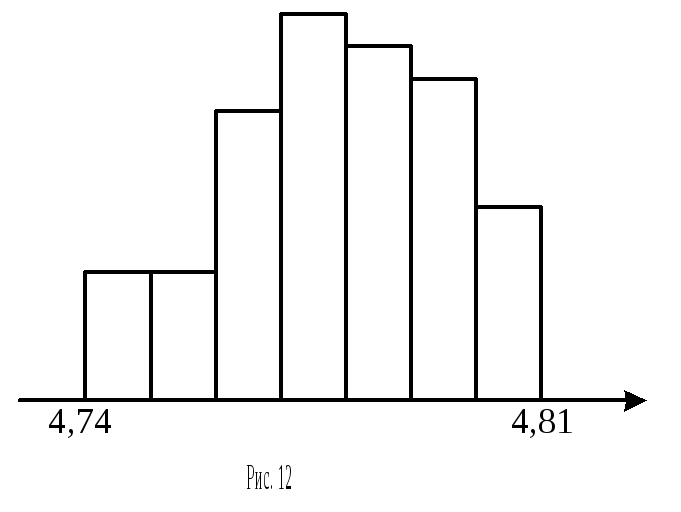
Результаты группированного статистического ряда можно использовать для построения гистограммы. Она строится следующим образом. По оси ОХ откладывают длины разрядов и над каждым разрядом строят прямоугольник, площадь которого равна частоте разряда. Так что суммарная площадь прямоугольников равна единице. Полученную диаграмму и называют гистограммой.

Пример. При измерении заряда электрона Милликеном было получено 58 измерений (в 10^-10 абс. эл. стат. единицах) 4,781; 4,795; 4,764; 4,769; 4,792; 4,792; 4,779; 4,764; 4,795; 4,775,… (ради упрощения мы привели только десять из этих измерений). Построить: 1) статистический ряд распределения; 2) статистическую функцию распределения; 3) группированный статистический ряд; 4) гистограмму; 5) найти средний заряд электрона и среднее значение квадрата ошибки измерений.

Решение. 1). Все 58 измерений есть выборка, приведенные 10 измерений – также выборка. Статистический ряд построим для десяти измерений.

Xi	4,764	4,769	4,775	4,779	4,781	4,792	4,795

2

) Статистическую функцию построим также для десяти измерений (см. рис. 11).

3) В случае 58 измерений размах выборки R=4,810-4,740=0,07. Разобьем весь этот диапазон значений на 7 равных разрядов, подсчитаем частоту каждого разряда и получим следующий группированный статистический ряд:

Разряды	4,74-4,75	4,75- 4,76	4,76-4,77	4,77-4,78	4,78-4,79	4,79-4,80	4,80-4,81
Частота

4) Ширина каждого из семи прямоугольников в гистограмме равна 0,01, а высоты равны соответствующей частоте, умноженной на 100 (см. рис. 12).

5) Для оценки заряда электрона воспользуемся формулой (1).

При n=10 получим =4,7807, а при n=58 =4,7808.

Для оценки квадрата ошибки измерений воспользуемся формулой (3) при k = 2, только n заменим в ней на (n – 1). Причина этого будет ясна позже. При n = 10 получим а при n = 58