Раздел II

Поиск недостающих данных ряда динамики осуществляется по одной из формул, в зависимости от вида ряда:

(2.1)

(2.2)

где - уровень динамического ряда в i-ом году;

- уровень динамического ряда в (i-1)-ом году;

- средний коэффициент роста;

- число уровней ряда в данном периоде;

- уровень динамического ряда 1996 года;

- уровень динамического ряда 1991 года.

Абсолютные приросты (цепной и базисный):

(2.3)

(2.4)

где - цепной абсолютный прирост;

- базисный абсолютный прирост;

- уровень показателя в i-том периоде;

- уровень показателя в предыдущем, (i-1)-том периоде;

- уровень показателя в базисном периоде.

Коэффициенты роста (снижения) и прироста (цепной и базисный):

(2.5)

(2.6)

где - цепной коэффициент роста;

- базисный коэффициент роста.

(2.7)

(2.8)

где - цепной коэффициент прироста;

- базисный коэффициент прироста.

Темпы роста (цепной и базисный):

(2.9)

(2.10)

где - цепной темп роста;

- базисный темп роста.

Темпы прироста (цепной и базисный):

(2.11)

(2.12)

где - цепной темп прироста;

- базисный темп прироста.

Абсолютное значение одного процента прироста:

(2.13)

где - абсолютное значение одного процента прироста.

Средний уровень ряда (средней хронологической):

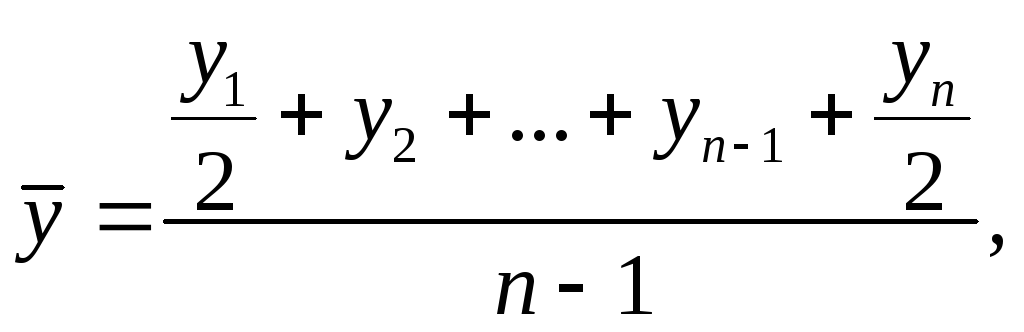(2.14)

где - средний уровень ряда;

– уровни ряда;

- число уровней.

Средний абсолютный прирост:

(2.15)

где - средний абсолютный прирост;

– абсолютный прирост цепной;

– число уровней.

Средние коэффициенты роста и прироста:

(2.16)

(2.17)

где - средний коэффициент роста;

- цепные коэффициенты роста;

- базисный коэффициент роста в последнем периоде;

- средний коэффициент прироста.

Средние темпы роста и прироста:

(2.18)

(2.19)

где - средний темп роста;

- средний темп прироста.

Для выравнивания ряда динамики используется система уравнений, построенная по методу наименьших квадратов:

- если при построении ряда динамики имеется тенденция выравнивания по прямой, то система уравнений следующая:

(2.20)

где - уровни эмпирического ряда;

- коэффициенты;

- количество уровней ряда;

- порядковый номер периода или момента времени.

Для упрощения решения системы отсчет времени ведется от середины ряда, тогда и система принимает вид:

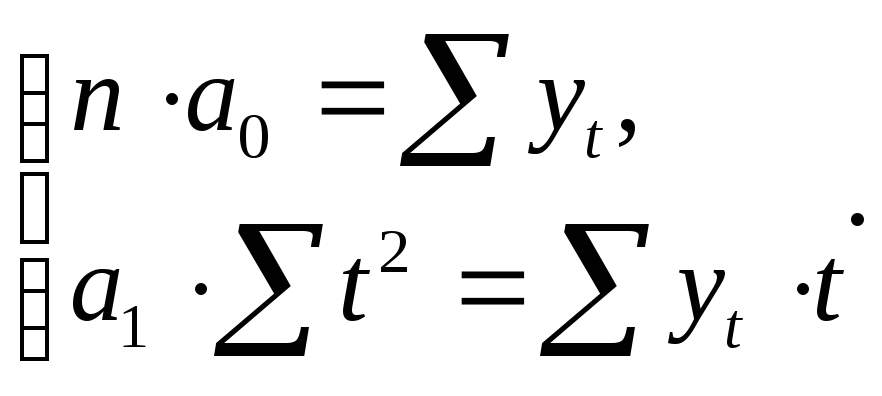(2.21)

Откуда:

(2.22)

(2.23)

- если при построении ряда динамики имеется тенденция выравнивания по параболе, то система уравнений следующая:

(2.24)

Для упрощения решения системы отсчет времени ведется от середины ряда, тогда , и система принимает вид:

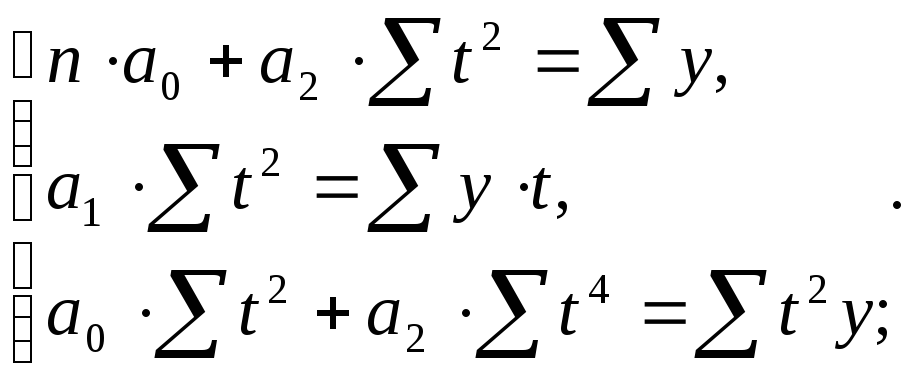(2.25)

Отклонение от прогнозных значений:

(2.26)

(2.27)

где – отклонение от прогнозных значений;

– коэффициент доверия (t=2);

- среднее квадратическое отклонение;

- уровни эмпирического ряда;

- средняя эмпирического ряда;

– число периодов;

– число параметров уравнения (для прямой m=2).