2. Модель судна – модель Номото

Одной из распространенных моделей описания движения судна на курсе является нелинейная модель Номото второго порядка:

, (2.28)

где .

Компонентами и как правило, пренебрегают и рассматривают модель в виде:

. (2.29)

Нелинейная математическая модель создает определенные трудности при анализе и синтезе систем автоматического управления. Поэтому в большинстве ситуаций при анализе систем стабилизации курсв нелинейным членом в уравнении (2.25) пренебрегают. В результате описание движения судна по угловой скорости становится линейным:

. (2.30)

Или в виде передаточной функции можно записать:

, (2.31)

где - курс судна, - угол отклонения пера руля, , , , - динамические параметры.

Эта модель может быть упрощена и приведена к модели Номото первого порядка:

, (2.32)

где .

3. Модель рулевой машины

На большинстве судов перо руля имеет ограничение на максимальный угол поворота – 35⁰ в каждую сторону. Учет данного фактора вводит нелинейность типа насыщение в схему рулевой машины. Кроме того скорость поворота пера руля ограничивается до 5⁰/сек в каждую сторону. Также система управления положением руля, как правило, является следящей, т.е. в ней присутствует обратная отрицательная связь.

С учетом приведенных ограничений модель рулевой машины имеет вид, приведенный на рисунке 2.3.

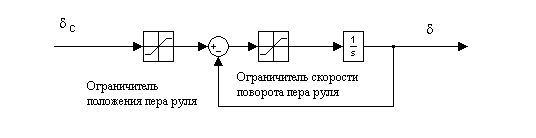
Рисунок 2.3. Модель рулевой машины

Ещё одной моделью рулевой машины является модель, когда ограничитель скорости поворота руля задаётся релейной характеристикой с зоной нечувствительности (рис. 2.4).

Рисунок 2.4. Модель рулевой машины

Математическая модель рулевой машины может быть представлена в виде следующего соотношения:

, (2.33)

где - сигнал регулятора, - функция ограничителя пера руля (зона линейности с ограничением), - функция ограничителя скорости поворота пера руля (в зависимости от типа рулевой машины: либо зона линейности с ограничением, как в первом случае, либо релейная характеристика с зоной нечувствительности, как во втором случае).

4. Модель внешней среды

На судно в той или иной мере действует ветро-волновое возмущение, вызванное погодными условиями и волнением моря. Модели такого возмущения могут быть представлены в виде суммы гармонических составляющих (сильное и наложенное на него слабое морское волнение) и постоянной составляющей (снос из-за ветра).

, (2.34)

где - постоянная составляющая, , - амплитуда и частота сильного морского волнения, , - амплитуда и частота слабого волнения.

6. Моделирование дискретных систем. Преобразование непрерывных линейных систем к дискретной форме

Известно, что схемы моделирования дискретных систем могут быть составлены по передаточным функциям или разностным уравнениям.

Рассмотрим метод составления структурных схем, основанный на замене оператора непрерывного интегрирования оператором численного интегрирования. В зависимости от используемой информации, применяются несколько операторов численного интегрирования.

Метод прямоугольников или прямой метод Эйлера:

, (1)

метод прямоугольников или обратный метод Эйлера:

(2)

метод трапеций:

. (3)

Используя, вышеприведенные операторы (выражения (1-3)), можно перейти от структурной схемы непрерывной системы к структурной схеме дискретной системы. Для того, что бы фазовые координаты дискретных систем отображали физические величины реальной (аналоговой) системы, непрерывные передаточные функции должны быть представлены детализированными структурными схемами (ДСС).

Если использовать только вышеперечисленные методы составления структурных схем дискретных систем регулирования, то не представляется возможным создать дискретную модель идентификатора. Поэтому рассмотрим еще один метод составления структурных схем, который позволяет так обосновать структуру дискретной модели, что ее фазовые координаты будут соответствовать физическим величинам аналоговой системы.

Этот метод основан на сравнении динамических характеристик непрерывной и дискретной моделей. Как известно, в пространстве состояния непрерывная модель задается матричными уравнениями:

(4)

где - матрица коэффициентов, управления и выхода дискретной системы; - фазовые координаты аналоговой системы; - выходная величина аналоговой системы.

Теперь разработаем процедуру получения дискретной модели по ее аналоговому эквиваленту, сохранив физический смысл аналоговых переменных состояния, только придав им дискретную форму. Запишем общее решение матричного уравнения (4), используя формулу Коши

, (5)

так как - выход экстраполятора, то на интервале сохраняет постоянное значение . Определим в конце интервала дискретности при

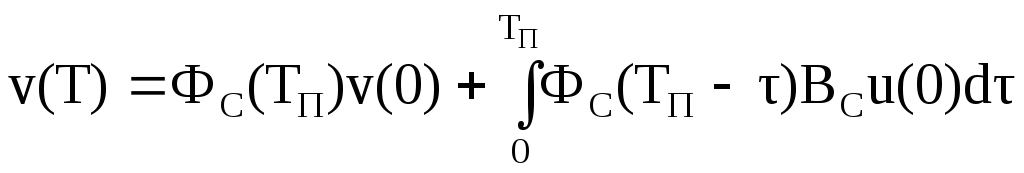. (6)

Определим для дискретной модели в конце первого интервала дискретности, используя выражения

. (7)

Чтобы координаты дискретной системы совпадали с соответствующими координатами аналоговой системы, должны выполняться следующие соотношения:

(8)

В этом случае выражения (6) и (7) при будут совпадать, что приведет к совпадению дискретных фазовых координат с аналоговыми.

Выразим выходную величину аналоговой системы при через фазовые координаты и матрицу :

.

Так как выходные координаты аналоговых и дискретных систем совпадают, то выполнение условия приводит к равенству матриц и :

.