Арифметика в позиционных системах счисления.

Арифметические действия над числами, записанными с помощью позиционной системы счисления, производятся по тем же правилам, что и в десятичной системе. Эти действия основаны на одинаковых правилах действий над многочленами.

Можно выполнять арифметические действия с многозначными числами, используя стандартные приемы поразрядных действий («в столбик»). В частности, сохраняются правила «переноса» значения в следующий разряд и «заимствования» значения из старшего разряда при сложении и вычитании.

Если требуется выполнить арифметические действия с числами, заданными в разных системах счисления, сначала надо преобразовать данные числа к одной системе счисления, а затем выполнять действия.

Рассмотрим следующий пример, использующий шестеричную систему счисления.

123554₆ + 212241₆ = 340235₆

Комплексные числа

Можно считать, что действительное число есть радиус-вектор, начинающийся в начале координат и заканчивающийся в точке числовой оси, соответствующей этому числу. Тогда множество R будет являться множеством радиусов векторов точек числовой оси.

Рассмотрим множество радиусов векторов точек плоскости, содержащей числовую ось. Это множество обозначается буквой K.

y

Z = a + ib

bi (a, b)

i



0 1 a x

Надо определить операции для К. Пусть операция сложения + совпадает с обычным сложением векторов. Для действительных чисел так определенная операция сложения совпадает с обычным сложением. Для произвольного элемента z множества К через z обозначим длину соответствующего радиус-вектора и будем назвать модулем z. Через α = arg z обозначим угол между направлением оси действительных чисел и направлением радиус-вектора. Элементы из К будем называть комплексными числами.

Произведением z₁, z₂ двух комплексных чисел называется комплексное число z, модуль которого равен z = z₁z₂, а аргумент arg z = arg z₁ + arg z₂.

Как сложение, так и умножение коммутативно и ассоциативно, так как все эти операции сводятся к умножению модулей, сложению аргументов и сложению векторов. Кроме того, справедлив и закон дистрибутивности .

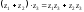Для действительных чисел новые правила сложения и умножения совпадают со старыми.

Любое комплексное число z единственным образом представимо в виде 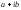, где a и b — действительные числа, откладываемые по горизонтальной и вертикальной осям соответственно, .

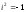a — действительная часть комплексного числа;

ib— мнимая часть комплексного числа;

b — коэффициент при мнимой части.

Для такого представления комплексных чисел справедливы следующие соотношения:

(a + ib) + (c + id) = (a+c) + i(b+d),

(a + ib)(c + id) = (ac bd) + i(cb+ad).

Очевидно, что 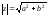и ,

.

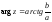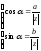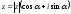— тригонометрическая форма комплексного числа.

Тригонометрическая форма представления комплексных чисел удобна для выполнения операций умножения и возведения в степень.

.

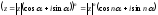При извлечении корня n-той степени из комплексного числа z используется формула Муавра:

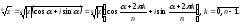
Отсюда ясно, что для любого комплексного числа z0 существует n различных значений корней n-той степени.

Если z = a + bi любое комплексное число, то 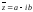комплексное число с тем же модулем и с аргументом противоположным по знаку аргументу z. Такое число называется сопряжённым z. Нетрудно проверить, что для любых комплексных чисел z и y справедливы соотношения: 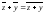и .

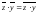Впервые "мнимые числа" появились в книге "Алгебра" итальянского математика Рафаэля Бомбелли (1530-1572), изданной в год смерти ученого. В этой книге дано изложение простейших правил действий над ними и их применение к исследованию кубического уравнения в случае, когда уравнение имеет три действительных корня, а в формуле, определяющей эти корни, присутствует квадратный корень из отрицательного числа. Однако, для многих крупных ученых XVII в., включая И. Ньютона (1643-1727) и Г. Лейбница (1646-1716), алгебраическая и геометрическая сущность комплексных чисел оставалась загадочной и мистической. А. Муавр (1667-1754) вывел для комплексных чисел приведенную выше формулу возведения в натуральную степень и извлечения корня с натуральным показателем. Эта формула нашла широкое применение в тригонометрии.

Символ i=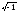 введен в 1777 г. Л. Эйлером (1707-1783), термин "комплексное число" ввел в 1803 г. Л. Карно (1753-1823) Полное геометрическое истолкование комплексных чисел и действий над ними дал в 1799 г. датский математик К. Вессель (1745-1818). Наиболее эффективное применение комплексных чисел в математике осуществили в XVIII - XIX вв. Л. Эйлер и К. Ф. Гаусс, доказавшие, что любой многочлен с действительными или комплексными коэффициентами имеет во множестве комплексных чисел хотя бы один корень. Этот результат впоследствии был назван "основной теоремой алгебры". Ф. Гаусс построил теорию целых комплексных чисел, с помощью которой были получены новые результаты и даны более простые доказательства известных теорем для обычных целых чисел.

В XIX в. и особенно в XX в. комплексные числа нашли широкое применение не только в различных областях математики, но и в механике, и в физике. В настоящее время теория функций комплексного переменного широко используется в теории упругости, аэро- и гидродинамике, электростатике, картографии, электротехнике и др. областях естествознания. Наиболее глубокие результаты были получены выдающимися русскими учеными Г В. Колосовым (1867-1936), Н. Е. Жуковским (1847-1921), С А. Чаплыгиным (1869-1942), М. В. Келдышем (1911-1978) и М.А. Лаврентьевым (1900-1980).

Н. Е. Жуковский и С. А. Чаплыгин успешно применили методы теории функций комплексного переменного к расчету профиля крыла самолета.

17