Производные основных элементарных функций

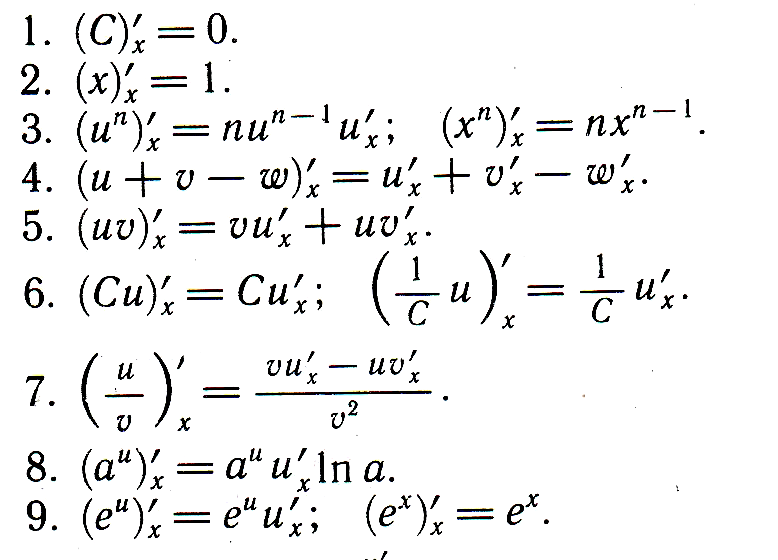
Дифференцирование сложной функции

Рассмотрим сложную функцию с одним промежуточным ар­гументом: y = f(u), u = φ(x), предполагая при этом, что функция y дифференцируема по аргументу u, а функция u дифференцируема по аргументу x. Производная сложной функции определяется по формуле:

y'_x = y'_u ∙u'_x (6)

Совершенно аналогично может быть выведено правило диф­ференцирования сложной функции с двумя промежуточными аргументами и т.д.

Пример. Найти производную функции y = ln(1+x²).

Используя правило дифференцирования сложной функции (6), получим:

пусть u = 1+x² , тогда y = ln u .

3. Понятие дифференциала функции

Согласно определению производной от функции имеем:

На основании определения предела это означает, что Δу/Δх = у' + α(Δх), где Отсюда Δу = у' ∙ Δх + Δх ∙ α(Δх). Первое слагаемое в правой части это­го равенства стремится к нулю, как Δх (если у' 0), а второе слагаемое кроме Δх содержит в себе множитель α(Δх), который тоже стремится к нулю при Δх . Таким образом, первое слагаемое стремится к нулю медленнее второго, и поэтому его называют главной частью приращения функции Δу.

Определение. Главная часть приращения функции Δу, рав­ная произведению у' ∙ Δх, называется дифференциалом первого порядка от функции , соответствующим выбранным значениям х и Δх.

Обозначается так:

dy = у' ∙ Δх (7)

Это так называемая первая форма записи дифференциала.

Выясним геометрический смысл дифференциала. На схема­тическом графике функции (рис. 3) отмечены две точки: точка А с абсциссой x и точка В с абсциссой х + Δx. Производная от функции в точке А равна угловому коэффициенту касательной к графику в этой точке. Поскольку CD = АС ∙ tgφ = у' ∙ Δx, заключаем, что диффе­ренциал dy равен приращению ординаты касательной к графику , соответствующему значениям x и x + Δx .

Рис. 3

Каков же механический смысл дифференциала?

Если s = f(t) есть путь, пройденный материальной точкой за время t, то, как известно, производная ds/dt есть скорость движения в момент времени t. Тогда дифференциал пути ds = f ' (t) ∙ Δt приближенно равен пути, пройденному материаль­ной точкой от момента времени t до момента времени t + Δt, если пренебречь изменением скорости движения на этом промежутке времени.

Кроме первой формы записи дифференциала существует и вторая. Дифференциалом аргумента называется дифференци­ал функции у = х, т.е. dy = dx. Однако на основании первой формы дифференциала имеем dy = Δx. Следовательно, Δx = dx, и мы получаем, таким образом, вторую форму записи дифференциала:

dy = у' ∙ dx (8)

Вторая форма дифференциала обладает свойством инвари­антности относительно аргумента, т. е. не зависит от того, явля­ется ли аргумент x окончательным или промежуточным. Пояс­ним это на примере.

Пример. Пусть требуется вычислить дифференциал функ­ции y = (1 + tg x)⁸. Это можно осуществить двумя способами:

1. Найдем у'(х) по правилам дифференцирования сложной функции:

Тогда

2. Введем новую функцию U = 1 + tg x. Тогда y = U⁸, dy = 8U⁷ dU (как дифференциал функции у = у (u)).

Вычислим dU:

dU = U'_x dx = (1 + tg x) ' dx = (1/cos²x) dx

Следовательно, dy = 8(1 + tg x)⁷ ∙ (1/cos²x) dx,

т. е. результат совпадает с результатом, вычисленным по первому способу.

Первая форма дифференциала таким свойством не обладает.

Поскольку формально дифференциал отличается от произ­водной лишь множителем Δx или dx, его свойства являются отражением соответствующих свойств производной.

Пользуясь таблицей производных, мы можем написать табли­цу дифференциалов от основных элементарных функций.