
мет_указ_СР_ДЛ
.pdf
Федеральное агентство морского и речного транспорта
Федеральное бюджетное образовательное учреждение высшего профессионального образования
«Морской государственный университет им. адм. Г. И. Невельского»
Кафедра вычислительной техники
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к выполнению самостоятельных и контрольных работ по базовым основам информатики для студентов специальностей 18010062
"Кораблестроение, океанотехника и системотехника объектов морской инфраструктуры", 19060062 "Эксплуатация транспортно-технологических машин и комплексов", 13100062 "Нефтегазовое дело" и 15100062 "Технологические машины и оборудование"
Составила Я. В. Пафнутьева
Владивосток
2014
2
Введение
Одной из основных составляющих Болонского процесса является увеличение числа часов, отводимых на внеаудиторную самостоятельную работу обучающихся. Считается, что специалист с высшим образованием должен постоянно самостоятельно совершенствовать свои знания, чему соответствует концепция непрерывного образования (имеется в виду, что студент должен получить навыки самостоятельного овладения знаниями, их пополнения и обновления). Самостоятельная работа студентов делится на аудиторную и внеаудиторную.
Внеаудиторная самостоятельная работа определяется как способ активного, целенаправленного приобретения обучающимся новых для него знаний и умений без непосредственного участия в этом процессе преподавателя. Внеаудиторная самостоятельная работа обучающихся – планируемая учебная, учебно-исследовательская или научно-исследовательская работа, выполняемая во внеаудиторное время по заданию и при методическом руководстве преподавателя, но без его непосредственного участия.
Дидактические цели самостоятельных внеаудиторных занятий: систематизация и закрепление полученных теоретических знаний и практических умений; углубление и расширение теоретических знаний; формирование компетенций; развитие познавательных способностей; развитие активности: творческой инициативы, самостоятельности, ответственности и организованности; формирование самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации; развитие исследовательских умений.
В Концепции модернизации российского образования обозначена задача - подготовка компетентного специалиста. Решение этой задачи видится через реорганизацию учебного процесса, обеспечивающего возрастающую долю самостоятельной работы и создание новых дидактических подходов к освоению учебного материала.
Самостоятельная работа – это такое средство обучения, которое:
формирует у студента на каждом этапе его движения от незнания к знанию необходимый объем и уровень знаний, навыков и умений для решения определенного класса познавательных задач и продвижение от низших к высшим уровням мыслительной деятельности;
вырабатывает психологическую установку на самостоятельное систематическое пополнение своих знаний и выработку умений ориентироваться в потоке информации при решении новых познавательных задач;
является важнейшим условием самоорганизации и самодисциплины обучающегося в овладении различными методами профессиональной деятельности;
является важнейшим орудием педагогического руководства и управления самостоятельной познавательной деятельностью студента в процессе обучения.
3
Самостоятельной можно считать только ту работу, которая требует от обучающегося активности и самостоятельности. Эта работа выполняется при отсутствии точного инструктажа, разъяснения со стороны преподавателя, без контроля в открытой форме за ее выполнением.
Она требует сосредоточенности, умственных и практических действий, самостоятельности, степень которой зависит не только от содержания материала, но и от индивидуальных возможностей студента. Поэтому даже самые простые виды самостоятельных работ обуславливают действия, которые приходятся совершать самостоятельно. Одна из особенностей самостоятельной работы – это побуждение и вовлечение студентов в процесс активного учебного и научного познания.
Данное учебно-методическое пособие охватывает все основные разделы аудиторной и внеаудиторной самостоятельной работы, предлагаемые для выполнения кафедрой вычислительной техники студентам и курсантам технических специальностей морской академии и института защиты моря и охраны шельфа.
"Алгебра логики. Таблицы истинности."
Основным математическим аппаратом, используемым при анализе и синтезе дискретных элементов и устройств, является алгебра логики (булева алгебра, алгебра Буля). В алгебре логики широко используется понятие “высказывание”. Высказыванием принято называть простое повествовательное положение, о котором можно сказать, что оно ложно или истинно, но не то и другое одновременно. Любое высказывание можно обозначить, например, символом X и считать, что X=1 (ИСТИНА), если высказывание истинно, а X=0 (ЛОЖЬ), если высказывание ложно. Логическая (булева) переменная – такая переменная X, которая может принимать только два значения: X={0,1} (X={ЛОЖЬ,ИСТИНА}). Из двух простых высказываний X и Y (A или B) можно образовать более сложные высказывания, используя операции "И", “ИЛИ”, “НЕ”. Сложные высказывания также принимают значения “ИСТИНА” или “ЛОЖЬ”, т.е. 1 или 0.
Смысл логических операций над простыми высказываниями X и Y и значениями сложных высказываний можно представить в виде таблиц истинности.
Формулу логики высказываний, принимающую значение истинности И (истина) на любом наборе значений для пропозициональных перемен-
ных, входящих в формулу, называют тождественно-истинной формулой, или тавтологией.
Таблица истинности - это таблица, устанавливающая соответствие между всеми возможными наборами логических переменных, входящих в логическую функцию и значениями функции. Таблицы истинности применяются для вычисления истинности сложных высказываний, установления эквивалентности высказываний и т.д.
Основными логическими операциями (функциями) являются:

4
1)Инверсия (отрицание) – это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
2)Конъюнкция (логическое умножение) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
3)Дизъюнкция (логическое сложение) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
4)Импликация (логическое следование) – функция возвращает 0 только
когда первый операнд равен 1, а второй равен 0. A называется антецедентом (или условием), B – консеквентом (или следствием) материальной импликации.
5) Эквивалентность (равносильность) – функция возвращает 1 только когда оба операнда равны между собой.
Вычисление значений логических выражений выполняется в определенном порядке, согласно их приоритету:
действия в скобках;
инверсия;
конъюнкция;
дизъюнкция;
импликация
эквивалентность.
Также дополнительными базисными функциями являются:
6)Неравнозначность ("либо", сложение по модулю "2", строгая дизъюнкция, исключающее "или", антиэквивалентность) – функция дает 1 только когда первый операнд не равен второму операнду.
7)Штрих Шеффера (отрицание конъюнкции, и-не, антиконъюнкция) – функция возвращает 0 только когда оба операнда равны 1.
8)Стрелка Пирса (отрицание дизъюнкции, или-не, символ Лукашевича, функция Даггера, функция Вебба, отрицание антидизъюнкция) – функция возвращает 1 только когда оба операнда равны 0.
Неравнозначность по приоритету равна эквивалентности, ибо это отрицание эквивалентности. В классической булевой алгебре приоритеты операций,
кроме вышеперечисленных, не определяются и считаются равными: исключающее или, стрелка Пирса, штрих Шеффера - все равноприоритетны. Однако в конкретных прикладных задачах уже начинается расстановка приоритетов с помощью скобок.
Обозначения:
5
инверсия (не)
инверсия (не) A
инверсия (не) B
конъюнкция A и B
дизъюнкция A и B
импликация A и B
эквивалентность A и B
штрих Шеффера A и B
стрелка Пирса A и B
неравнозначность A и B (сложение по модулю 2)
not; не
A; not A; не А; A
B; not B; не В; B
A&B; AB; A•B; A /\ B; А и В
A \/ B; А+В; А или В
A B; A => B; А > B
A B; A~B; A <=> B; А В
(A & B); (A /\ B); А ! В; A B
(A \/ B); А / В; A B
A B; A \/ B; А \/\/ В
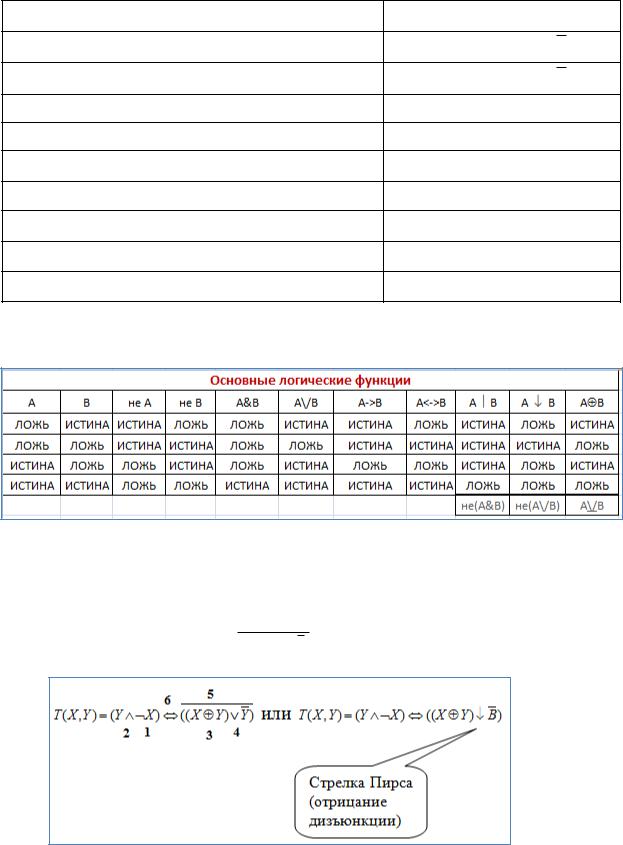
Таблицы истинности для логических функций двух переменных:
Таким образом, простые высказывания являются переменными, а более сложные высказывания – функциями. Причем как переменные, так и функции могут принимать только значения 0 (ЛОЖЬ) или 1 (ИСТИНА).
Задача 1. Построить таблицу истинности и вычислить значения логиче-
ской функции T (X ,Y ) (Y X ) (( X Y ) Y ) . Решение:
1) Необходимо расставить приоритет операций в формуле:
первая операция - не Х (в скобках);
вторая операция - конъюнкция Y и X (скобки);
третья операция - неравнозначность X и Y (скобки);
четвертая операция - дизъюнкция X и Y (скобки) и не Y;

6
пятая операция - отрицание дизъюнкции;
шестая операция - эквивалентность.
2)Построить таблицу истинности T(X,Y) и выполнить действия в соответствии с приоритетом:
Задача 2. Установить истинность высказывания
F
Ответ
(A B)
A & B
, по-
строив таблицу истинности. Решение:
1) Необходимо расставить приоритет операций в формуле:
первая операция - не А (в скобках);
вторая операция - импликация не А и В (скобки);
третья операция - конъюнкция А и В;
четвертая операция - отрицание конъюнкции А и В (штрих Шеффера);
пятая операция - дизъюнкция (логическое "или").
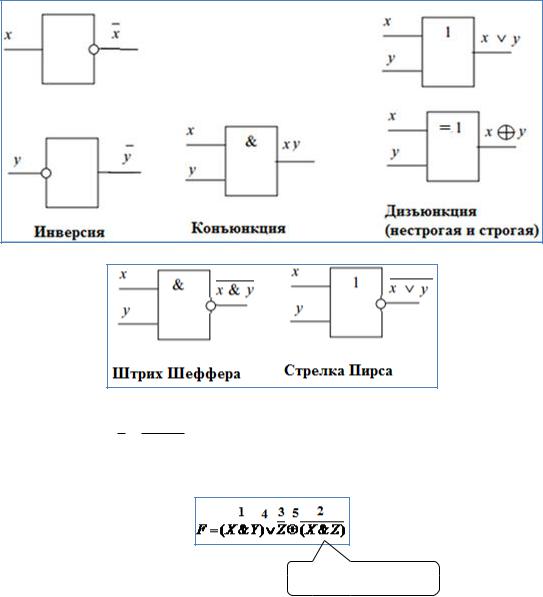
2)Построить таблицу истинности F и выполнить действия в соответствии с приоритетом:
Ответ
3) Истинность F при любых наборах значений А и В установлена.
7
Для работы с логическими функциями и построения таблицы истинности целесообразно использовать MS Excel 2007.
"Структурные логические схемы"
Алгебра логики дала конструкторам мощное средство разработки, анализа и совершенствования логических функций - это логические структурные схемы. Проще и быстрее изучать свойства и доказывать правильность работы схемы с помощью выражающей её формулы, чем создавать реальное техническое устройство.
Логические схемы, содержащие минимальное количество элементов, обеспечивают большую скорость работы и увеличивают надёжность устройства.
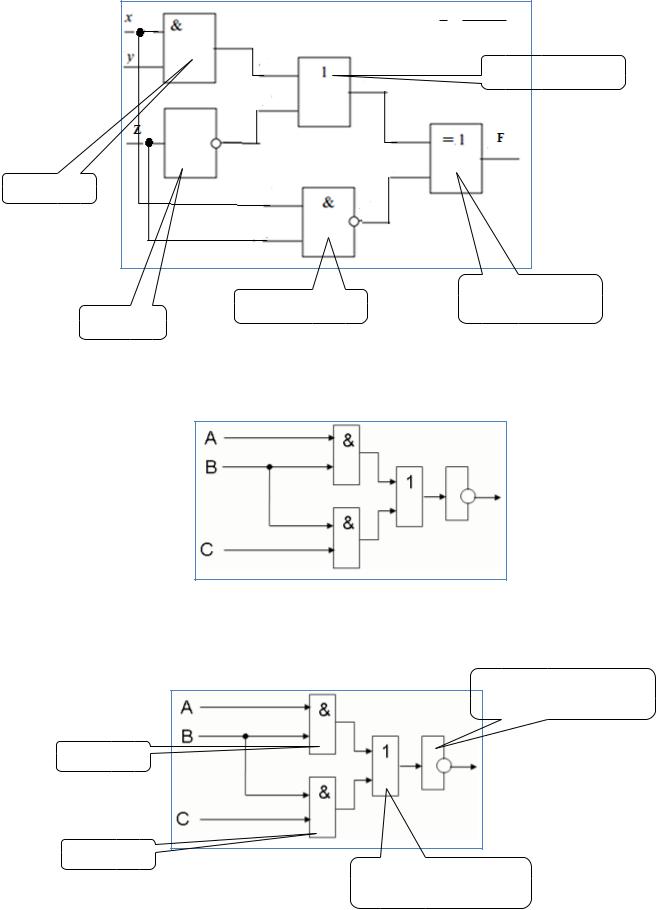
Обозначение базовых логических элементов в виде схем:
Задача 1. Построить логическую структурную схему по логической формуле F (X &Y ) Z (X & Z) . Решение:
1) Необходимо установить приоритет операций.
Штрих Шеффера
2) Выполнять построение схемы иногда целесообразно от конца.
8
F (X &Y ) Z (X & Z)
Дизъюнкция (4)
X & Y (1)
Не (X & Y) (2) |
Строгая |
|
дизъюнкция (5) |
||
Не Z (3) |
||
|
Задача 2. Составить логическое выражение F(A,B,C) по структурной логической схеме:
Решение:
1) Необходимо установить приоритет операций.
((A&B) \/ (B&C)) (4)
A & B (1)
B & C (2)
((A&B) \/ (B&C)) (3)

9
2) Выполнить пошагово построение выражения.
F (A,B,C) = 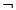 ((A & B) \/ (B&C)) или F(
((A & B) \/ (B&C)) или F(
Ответ:
A, B, C)
(A &
B)
(B & C)
.
"Формализация сложных высказываний"
Высказывание - это повествовательное предложение, о котором можно сказать, что оно истинно или ложно. Например:
Земля - планета Солнечной системы. (Истинно)
2+8<5 (Ложно)
Не всякое предложение является высказыванием:
1.Восклицательные и вопросительные предложения высказываниями не являются.
2.Не являются высказываниями и определения. Определения не бывают истинными или ложными, они лишь фиксируют принятое использование терминов.
3.Не являются высказываниями и предложения типа “Он сероглаз” или “х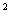 - 4х+3=0” - в них не указано, о каком человеке идет речь или для какого числа х верно равенство. Такие предложения называются высказывательными формами.
- 4х+3=0” - в них не указано, о каком человеке идет речь или для какого числа х верно равенство. Такие предложения называются высказывательными формами.
Некоторые высказывания можно разложить на отдельные части, при этом каждая такая часть будет самостоятельным высказыванием. Например, высказывание “Сегодня в 4 часа дня я был в институте, а к 6 часам вечера пошел на каток” состоит из 2 частей. Высказывание может состоять и из большего количества частей.
Высказывание, которое можно разложить на части, называется сложным, а неразложимое далее высказывание - простым. Неразложимое высказывание не может содержать отрицание, оно всегда должно быть утвердительным.
Сложное высказывание получается путем объединения простых выска-
зываний связками - частицей НЕ; союзами И; ИЛИ; НЕВЕРНО, ЧТО...; ТОГДА И ТОЛЬКО ТОГДА..., КОГДА...; ЕСЛИ..., ТО...:
№ |
Операция |
Обозначение |
Истолкование |
|
1 |
Инверсия |
(логиче- |
не А; |
Не А; |
|
ское отрицание) |
А; |
Неверно, что А |
|
|
|
|
A |
|
2 |
Конъюнкция (логи- |
AB; |
А и В; |
|
|
ческое произведе- |
A /\ B; |
Как А, так и В |
|
|
ние) |
|
A & B; |
А вместе с В; |
|
|
|
А и В |
А несмотря на В; |
|
|
|
|
А в то время как В |
3 |
Дизъюнкция (логи- |
А + В; |
А или В; |
|
|
ческое сложение) |
A \/ B; |
А или В, или оба |
|
|
|
|
А или В |
|
4 |
Строгая |
дизъюнк- |
А В; |
А либо В; |
|
ция (неравнознач- |
А \/ В |
А либо В, но не оба |
|

|
|
|
10 |
|
|
|
|
|
|
|
ность) |
|
|
|
5 |
Импликация (логи- |
А => B; |
|
Если А, то В; |
|
ческое следова- |
А В; |
|
В если А; |
|
ние) |
A > B |
|
В необходимо для А; |
|
|
|
|
А достаточно для В; |
|
|
|
|
В тогда, когда А |
6 |
Эквивалентность |
А = В; |
|
А эквивалентно В; |
|
(равнозначность) |
A B; |
|
А необходимо и достаточно для В; |
|
|
A ~ B |
|
А тогда и только тогда, когда В; |
|
|
|
|
А если и только если В |
|
|
|
|
А как В |
В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно. Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только 0 или 1. Если высказывание истинно, то его значение равно 1, если ложно - 0. Простые высказывания назвали логическими переменными, а сложные высказывания логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С и т.д.
Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний и объединяющих их связок.
Задача 1. Формализовать (записать) с помощью букв и знаков логических операций высказывание «У кошки четыре ноги». Это простое высказывание. Решение: А = 1.
Задача 2. Формализовать (записать) с помощью букв и знаков логических операций высказывание «Я полечу в Санкт-Петербург тогда, когда моя мама полетит в Москву». Это сложное (составное) высказывание. Решение:
1.А – «Я полечу в Санкт-Петербург».
2.В – «Моя мать полетит в Москву».
3.Ответ: В => А.
Задача 3. Формализовать (записать) с помощью букв и знаков логических операций фрагмент стихотворения М.Ю. Лермонтова:
«Нет, я не Байрон, я другой, Еще неведомый избранник,
Как он, гонимый миром странник, Но только с русскою душой».
Это сложное (составное) высказывание. Решение:
1.А – «Это - поэт Байрон».
2.B – «Это - ведомый людьми избранник».
3.C – «Гонимый миром странник».
4.D – «Странник с русской душой».
5.Ответ: ((A C) /\ D) /\ ( А /\ B) .
Задача 4. Формализовать (записать) с помощью букв и знаков логических операций слова А. Линкольна «Я одинаково не хочу быть ни рабом, ни
